
6. Ряды Тейлора
Пусть f(x) определена в некоторой окрестности точки x0 и имеет в этой точке производные любого порядка (бесконечно дифференцируема). Рядом Тейлора функции f(x) в окрестности точки x0 называется степенной ряд
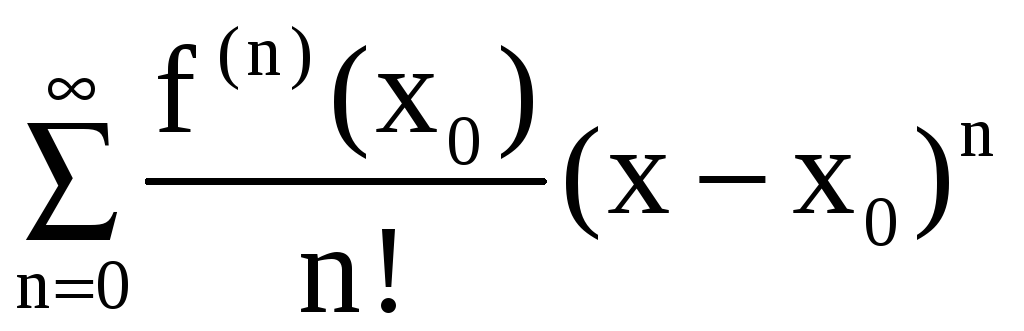
(при
этом полагаем
![]() ).
).
Теорема 10.
Если степенной
ряд
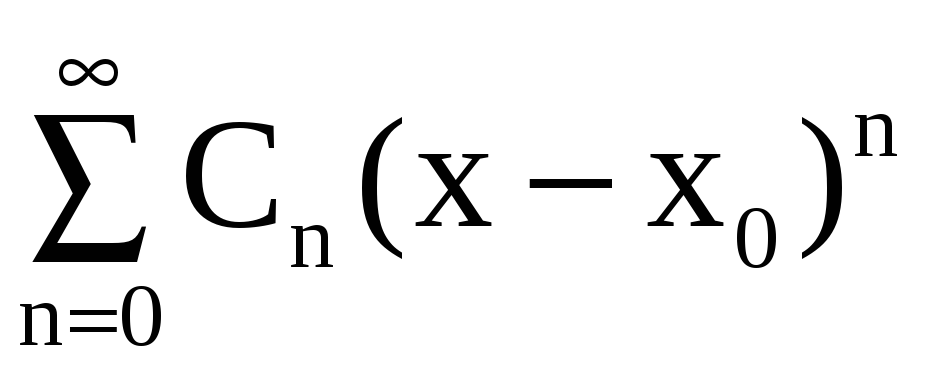 в некотором
в некотором
![]() интервале
интервале
![]() сходится к функции f(x)
(то есть
сходится к функции f(x)
(то есть
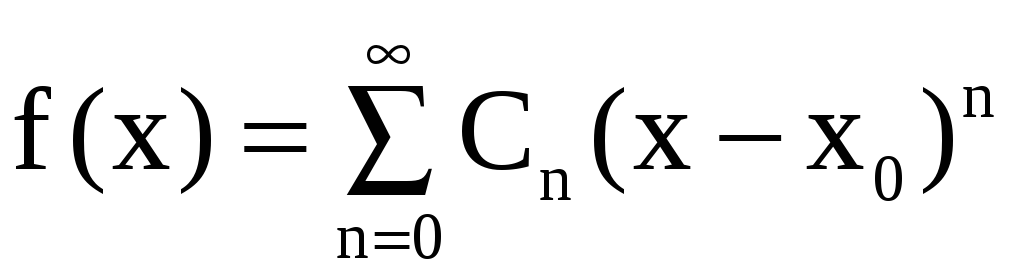 ),
то этот ряд является рядом Тейлора
функции f(x),
то есть
),
то этот ряд является рядом Тейлора
функции f(x),
то есть
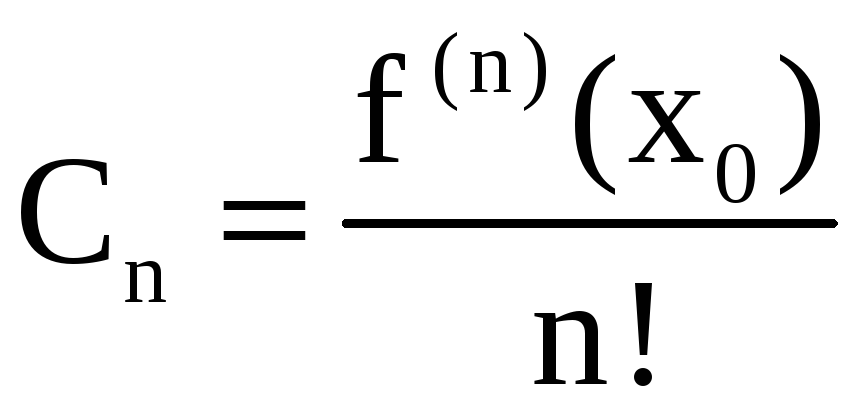 .
Тогда получим
.
Тогда получим
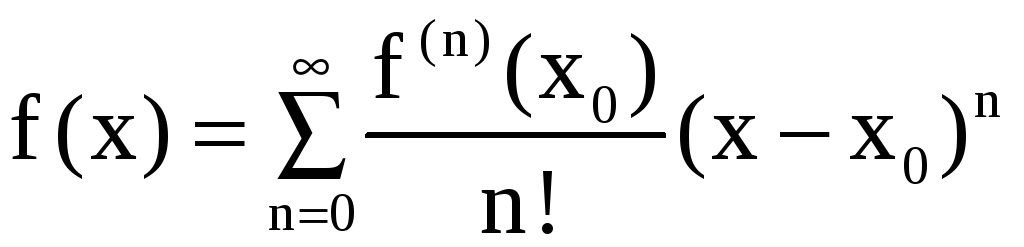 . (7)
. (7)
Не для всякой бесконечно дифференцируемой функции f(x) ряд Тейлора этой функции сходится к f(x). Достаточное условие для этого даёт следующая теорема.
Теорема 11.
Если f(x)
бесконечно дифференцируема в некоторой
окрестности точки x0
и существует такая постоянная величина
M
, что для любых n
N
и x
из этой окрестности
![]() ,
то f(x)
разлагается в ряд Тейлора:
,
то f(x)
разлагается в ряд Тейлора:
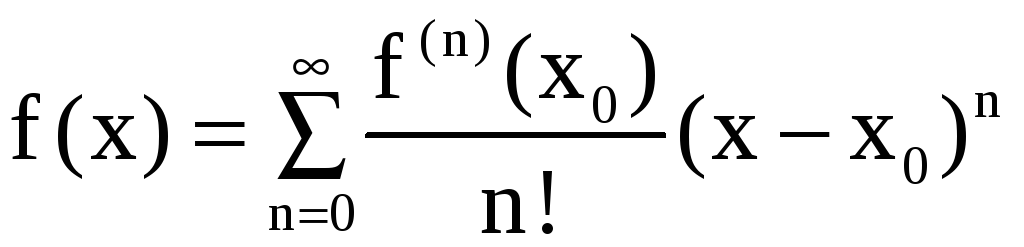 .
.
Известны следующие разложения некоторых элементарных функций в ряд Тейлора (в скобках указана область сходимости ряда):
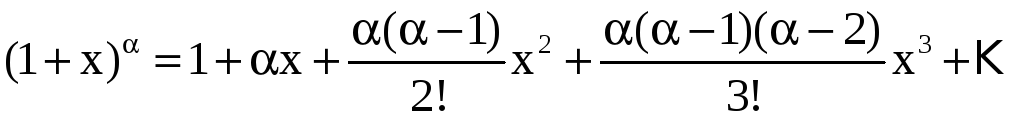
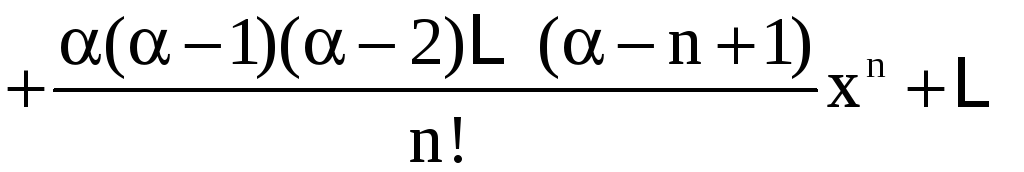 ,
, ![]() ;
;
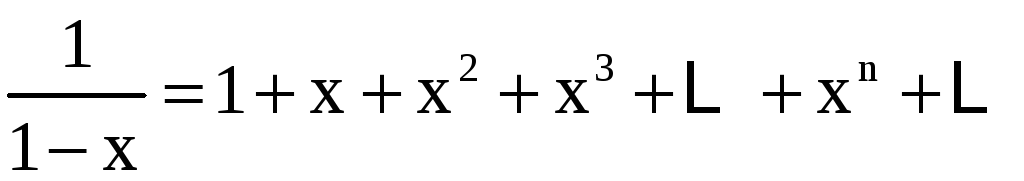 ,
, ![]() ;
;
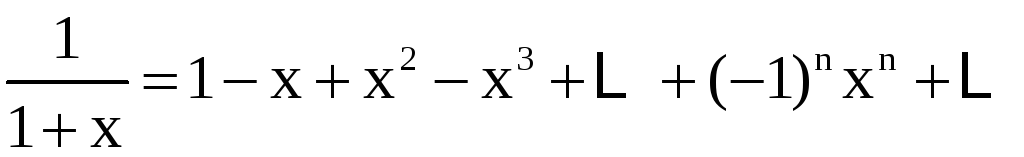 ,
, ![]() ;
;
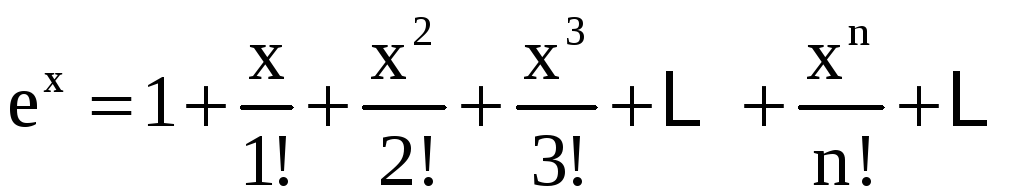 ,
(
,
(![]() ;
;
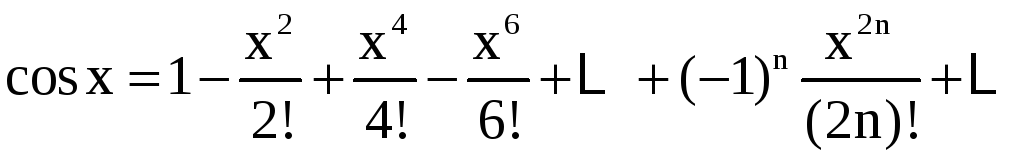 ,
(
,
(![]() ;
;
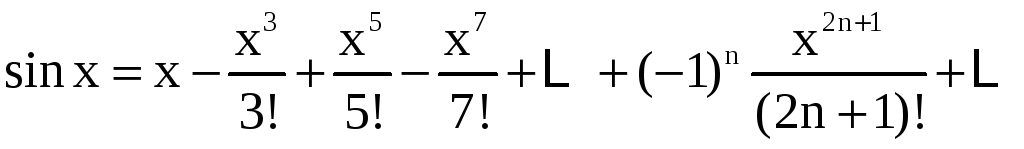 , (
, (![]() ;
;
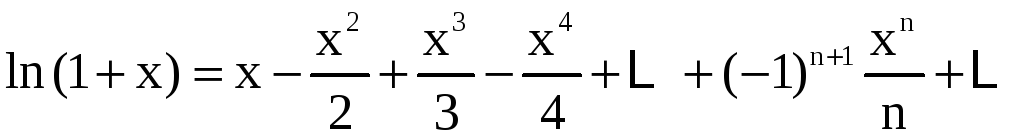 , (
, (![]() ;
;
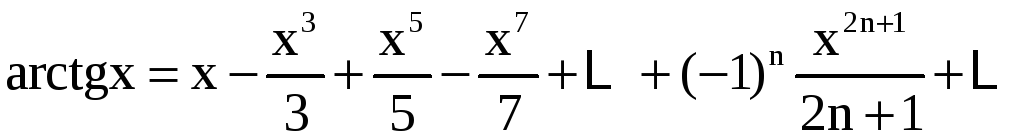 , (
, (![]() .
.
Пример 11. Разложить
функцию
![]() в ряд Тейлора по степеням x.
в ряд Тейлора по степеням x.
Решение. 1 способ. Разложить функцию по степеням x означает, что её нужно разложить в ряд Тейлора в окрестности точки x0= 0. Для этого найдём производные заданной функции и их значения в точке
x0 = 0. Займёмся этим.
![]() ,
,
![]() ;
;
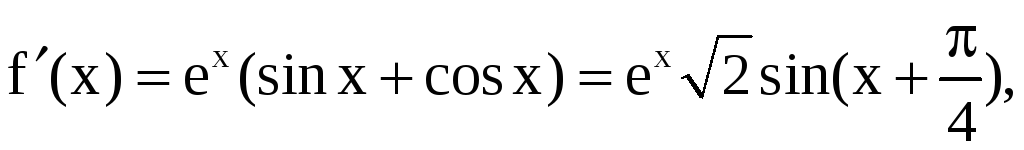
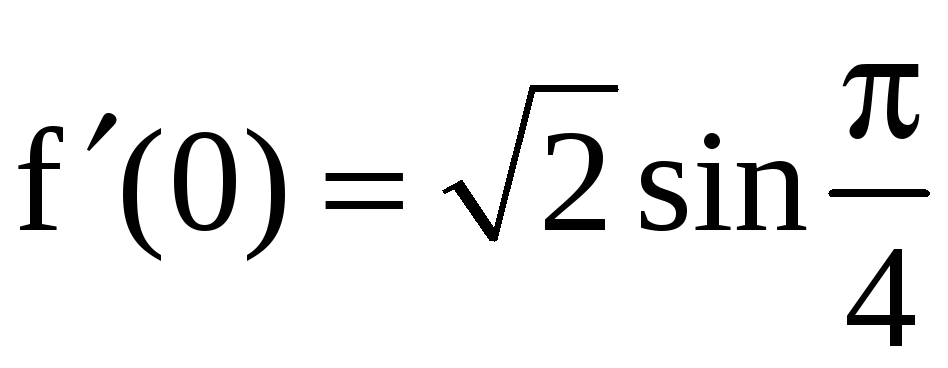 ;
;
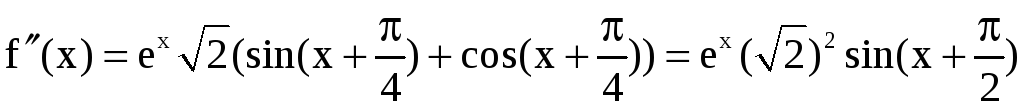 ,
,
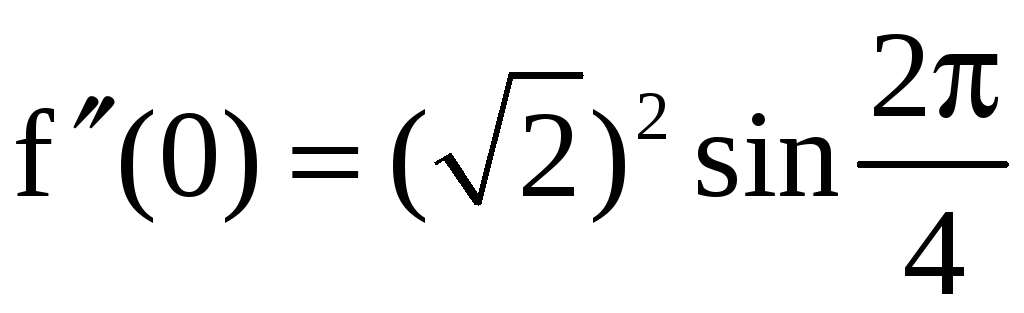 ;
;
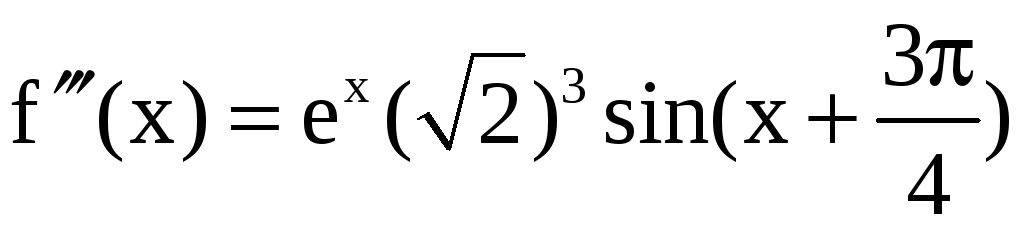 ,
,
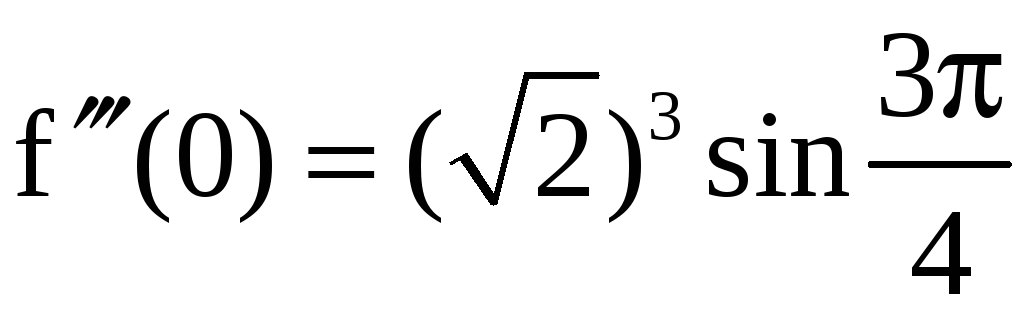 ;
;
. . . . . . . . .
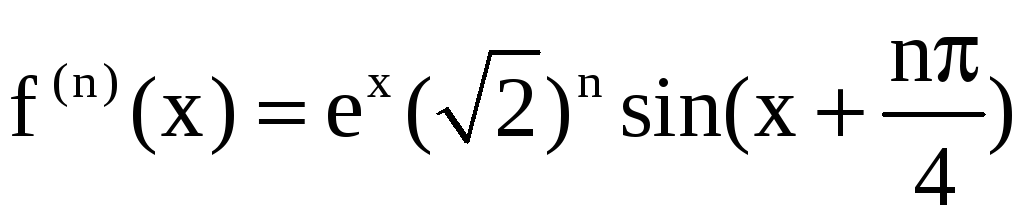 ;
;
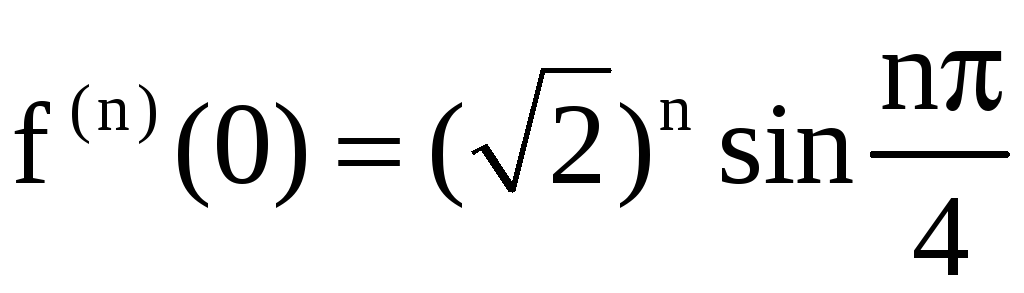 .
.
Найденные
значения
![]() подставим в (7), это даст нам требуемое
разложение f(x)
по степеням x:
подставим в (7), это даст нам требуемое
разложение f(x)
по степеням x:
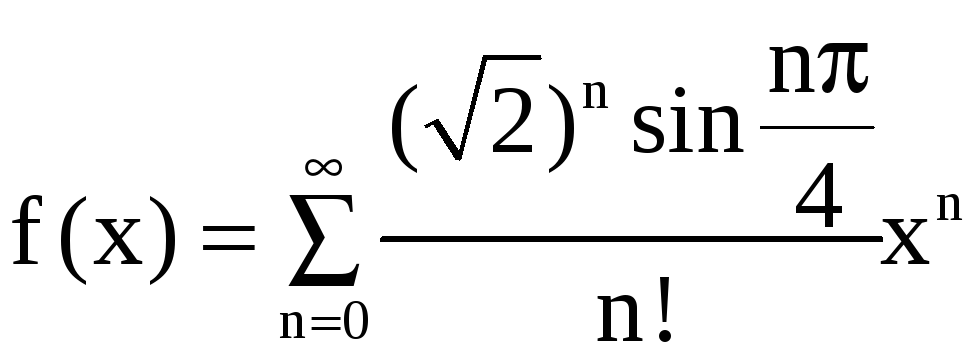 .
.
2 способ.
Воспользовавшись записанными выше
разложениями функций
![]() и sinx,
имеем
и sinx,
имеем
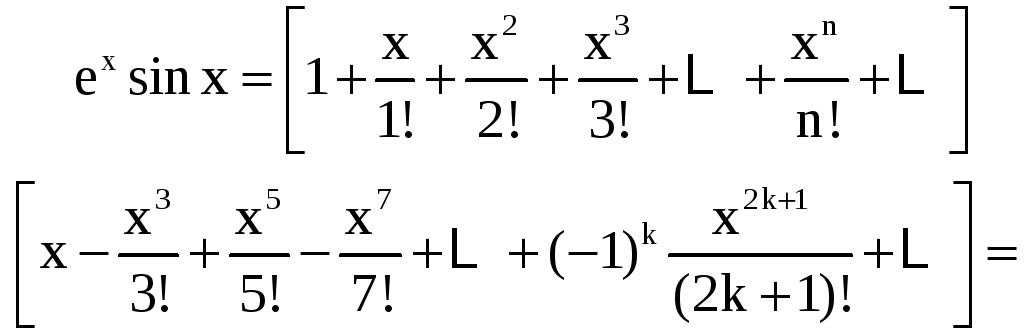
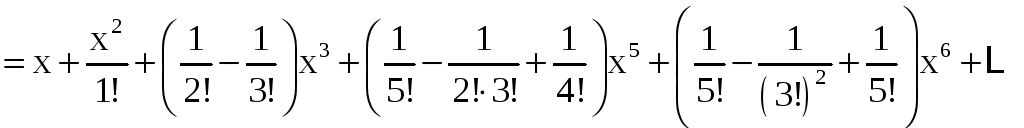
Замечание.
В последнем примере мы поставили знак
равенства между самой функцией
![]() и её рядом Тейлора. Вообще говоря, это
требует обоснования. Сформулируем ещё
одно достаточное условие для сходимости
ряда Тейлора функции f(x)
к самой функции f(x)
(более сильное, чем теорема 11).
и её рядом Тейлора. Вообще говоря, это
требует обоснования. Сформулируем ещё
одно достаточное условие для сходимости
ряда Тейлора функции f(x)
к самой функции f(x)
(более сильное, чем теорема 11).
Теорема 12. Пусть
f(x)
определена и непрерывна на отрезке
![]() и бесконечно дифференцируема на
и бесконечно дифференцируема на
![]() .
Обозначим
.
Обозначим
![]() .
Если
.
Если
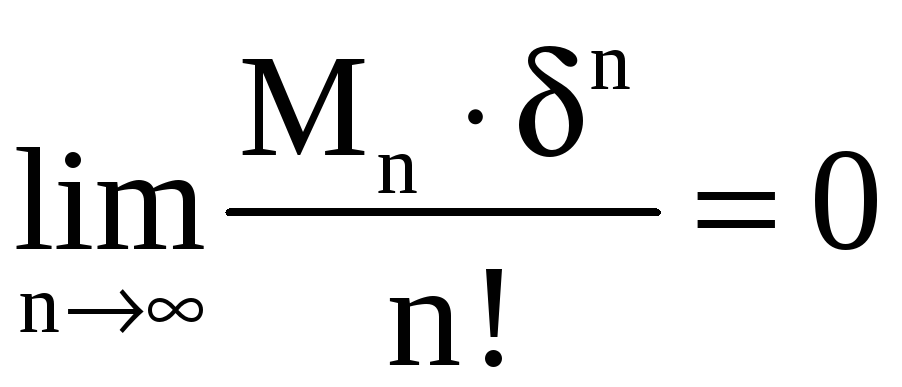 , (8)
, (8)
то
ряд Тейлора функции f(x)
на промежутке
![]() равномерно сходится к f(x):
равномерно сходится к f(x):
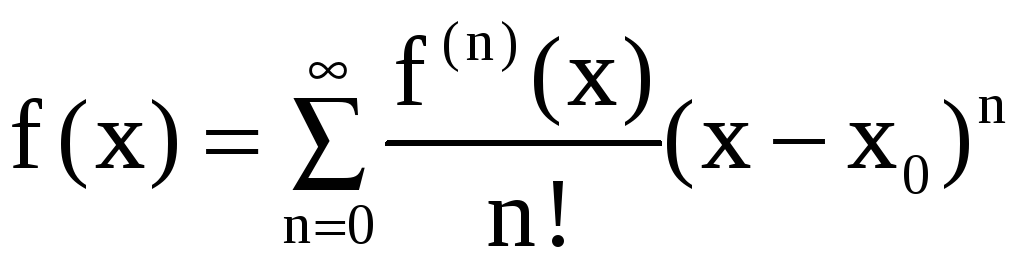 .
.
При
этом
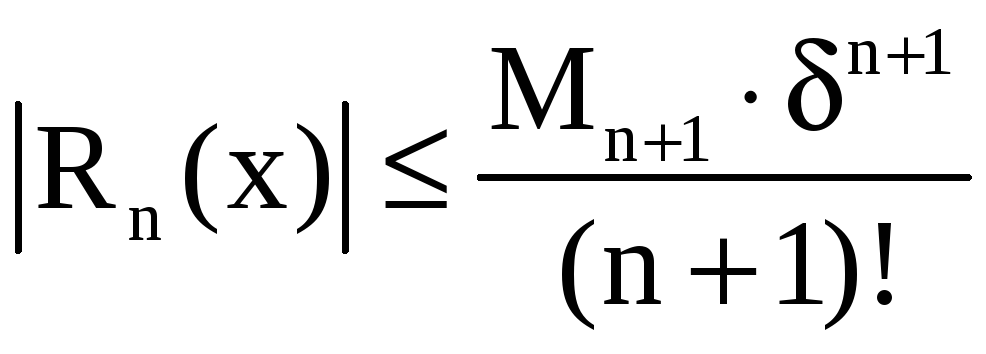 . (9)
. (9)
Покажем, что для
функции
![]() из примера 11 выполняется условие (8) при
любом конечном .
Действительно,
из примера 11 выполняется условие (8) при
любом конечном .
Действительно,
![]() ,
отсюда
,
отсюда ![]() . Несложно доказывается, что
. Несложно доказывается, что
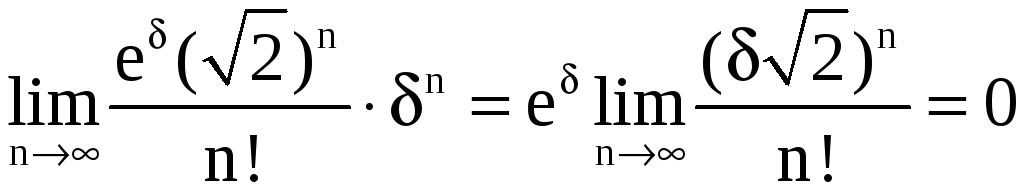 ,
,
откуда и следует справедливость вышеупомянутого равенства.
Пример 12. Разложить
функцию
![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням
![]() ,
используя разложения основных элементарных
функций.
,
используя разложения основных элементарных
функций.
Решение.
Выражение,
стоящее под знаком логарифма, преобразуем
таким образом, чтобы выделить выражение
![]() :
:
![]()
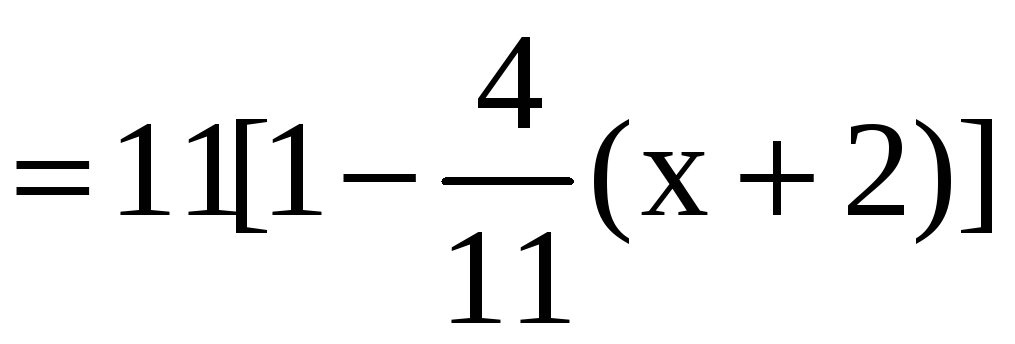 .
.
Тогда
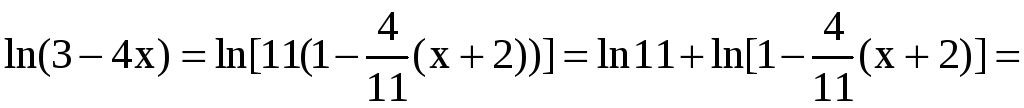
![]() ,
,
где
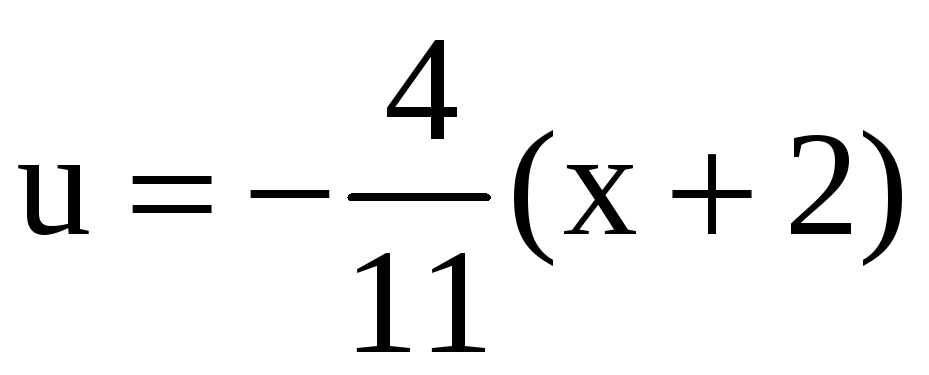 .
Теперь воспользуемся разложением в ряд
Тейлора для функции
.
Теперь воспользуемся разложением в ряд
Тейлора для функции
![]() при
при
![]() :
:
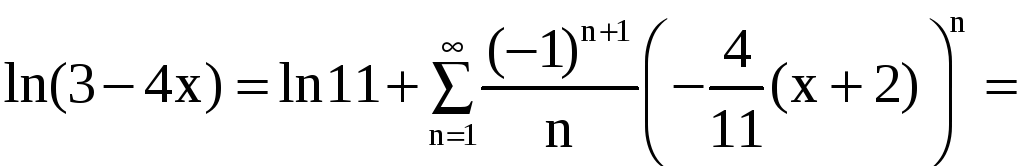
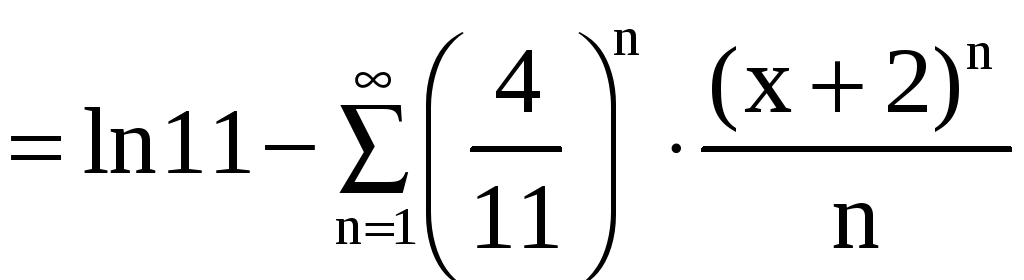 ,
, 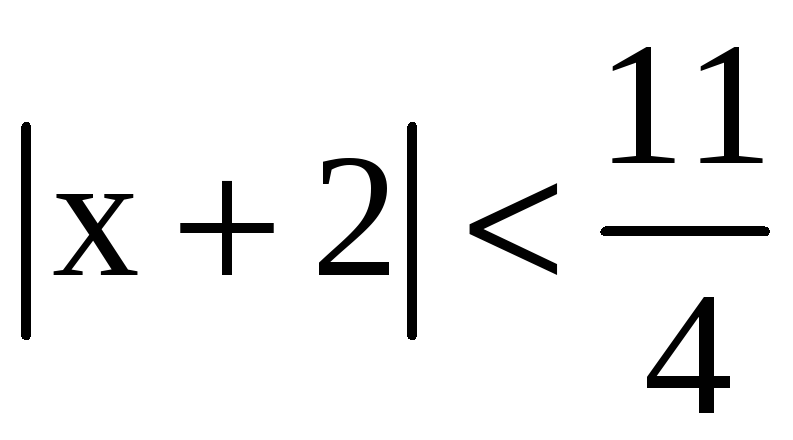 .
.
Исследуем
поведение ряда на концах интервала
сходимости
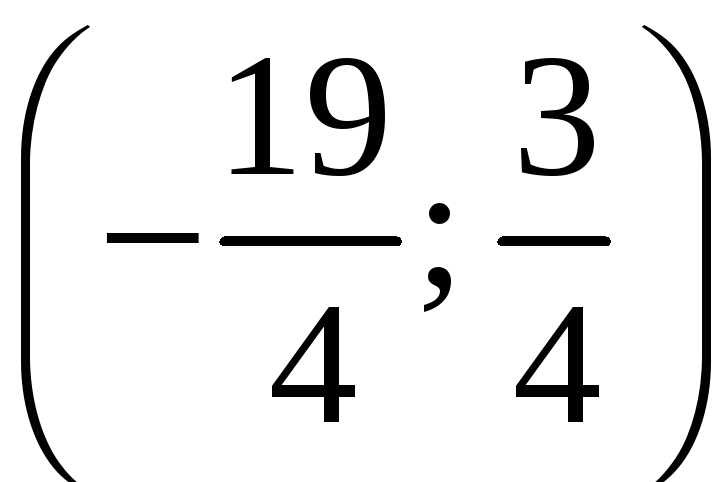 .
.
При
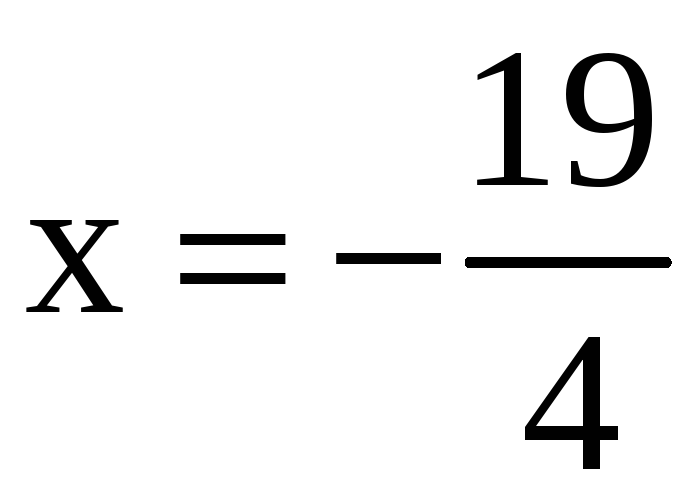 получаем знакочередующийся ряд
получаем знакочередующийся ряд
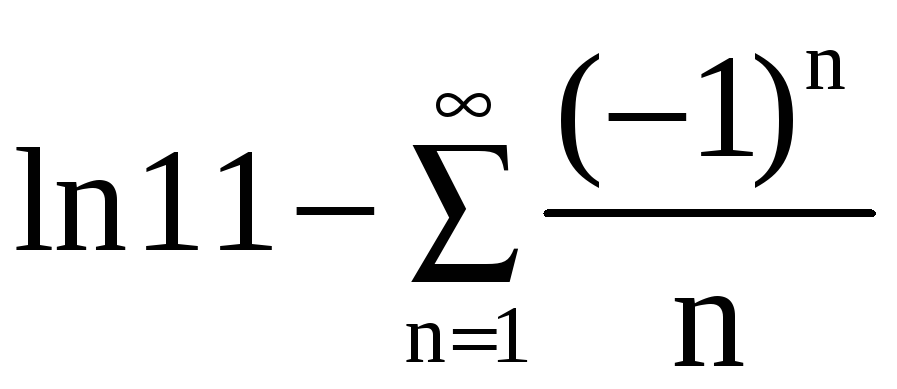 ,
сходящийся согласно признаку Лейбница.
При
,
сходящийся согласно признаку Лейбница.
При
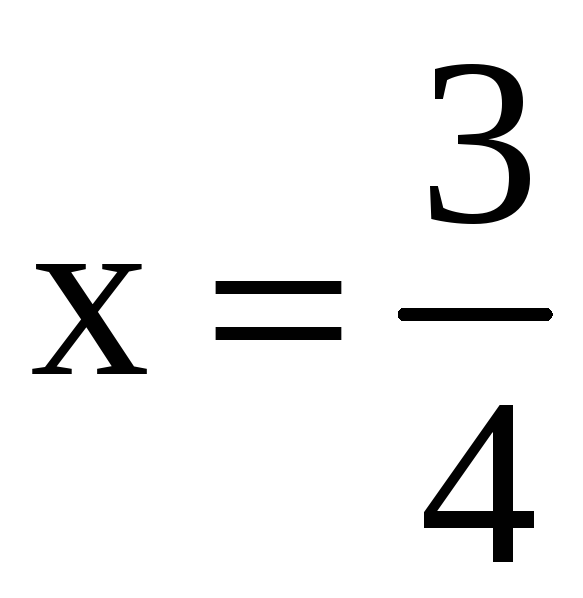 получаем гармонический ряд, который,
как известно, расходится. Таким образом,
полученный степенной ряд сходится на
промежутке
получаем гармонический ряд, который,
как известно, расходится. Таким образом,
полученный степенной ряд сходится на
промежутке
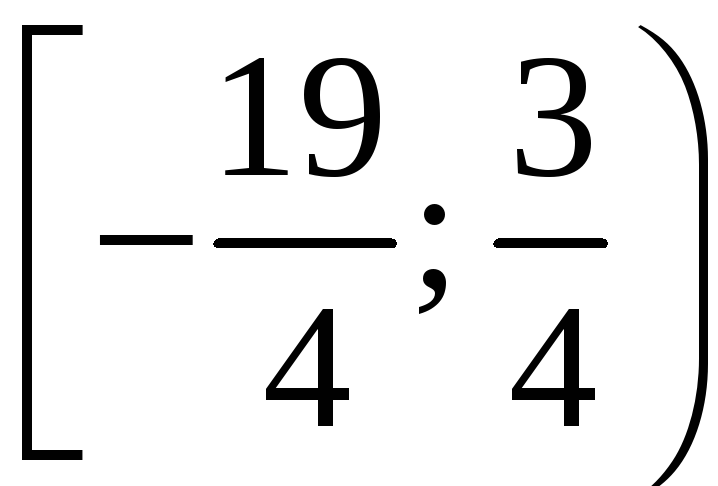 .
.
Пример 13.
Разложить функцию
![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки
![]() ,
используя разложение основных элементарных
функций.
,
используя разложение основных элементарных
функций.
Решение. Заданную функцию преобразуем следующим образом:
![]() .
.
Воспользовавшись
известными разложениями в ряд Тейлора
функций
![]() и
и
![]() ,
получим
,
получим
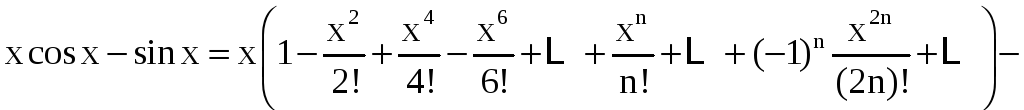
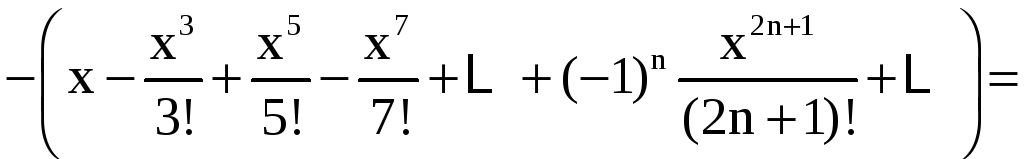
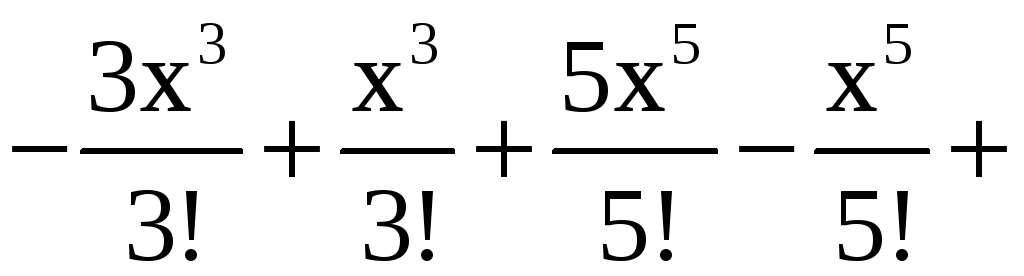
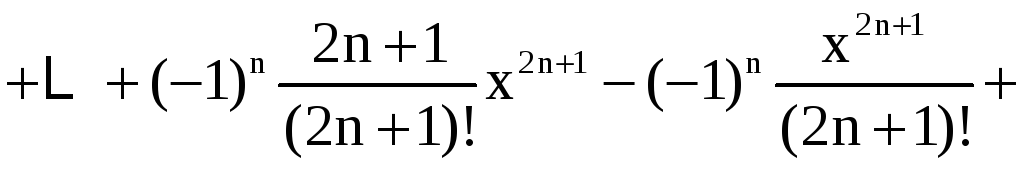

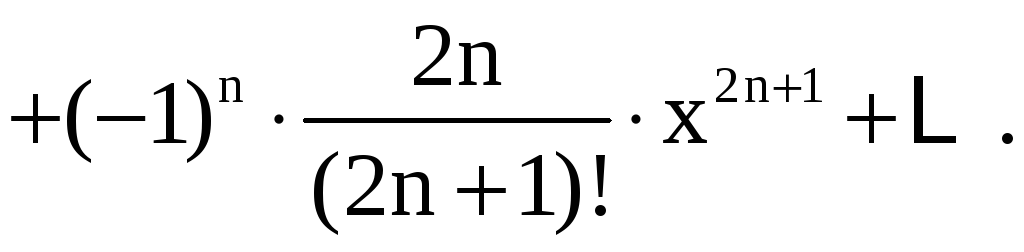
Так как ряды Тейлора для cosx и sinx сходятся при любых значениях x, то и полученный ряд функции f(x) будет сходиться для любых x.
Пример 14.
Разложить функцию
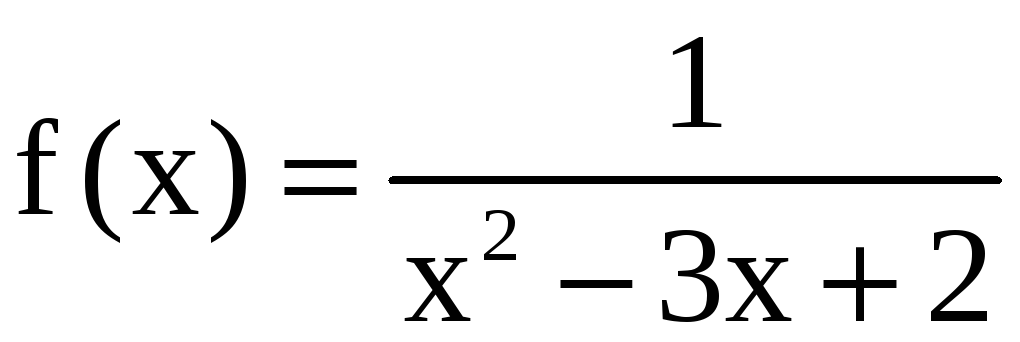 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки
![]() ,
используя разложение основных элементарных
функций.
,
используя разложение основных элементарных
функций.
Решение. Заданную функцию разложим на сумму простейших дробей:
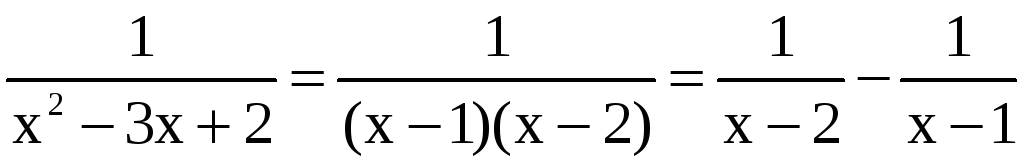 .
.
Полученные слагаемые можно представить в виде
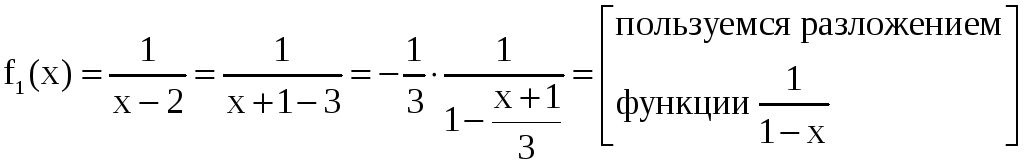 =
=
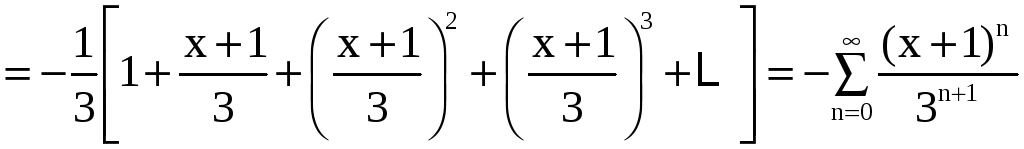 ,
,
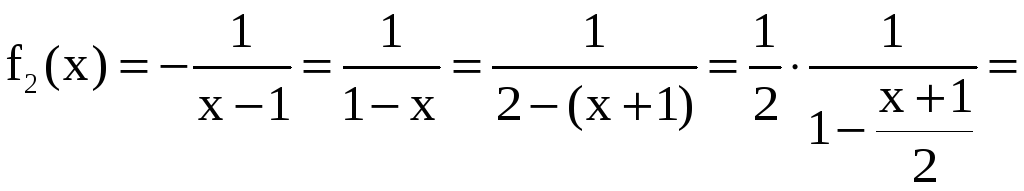
 .
.
Отсюда
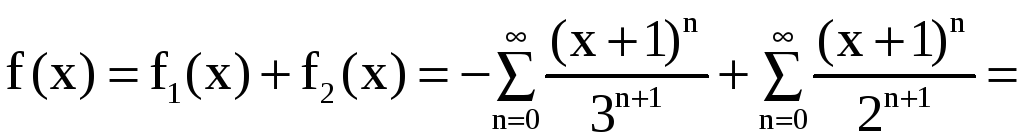
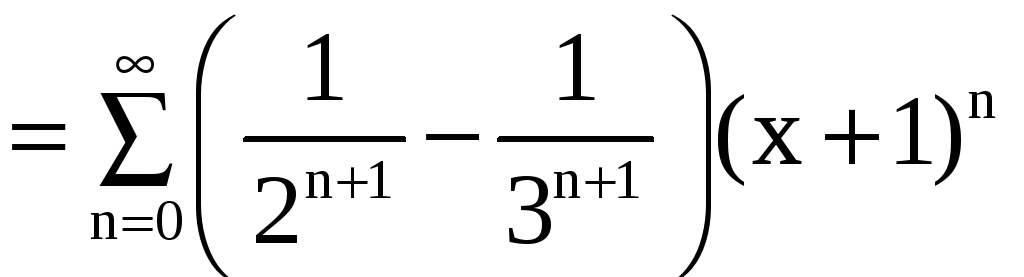 .
.
Осталось выяснить
интервал сходимости последнего ряда.
Он является пересечением областей
сходимости рядов Тейлора для функций
![]() и
и
![]() ,
то есть множеств, задаваемых неравенствами
,
то есть множеств, задаваемых неравенствами
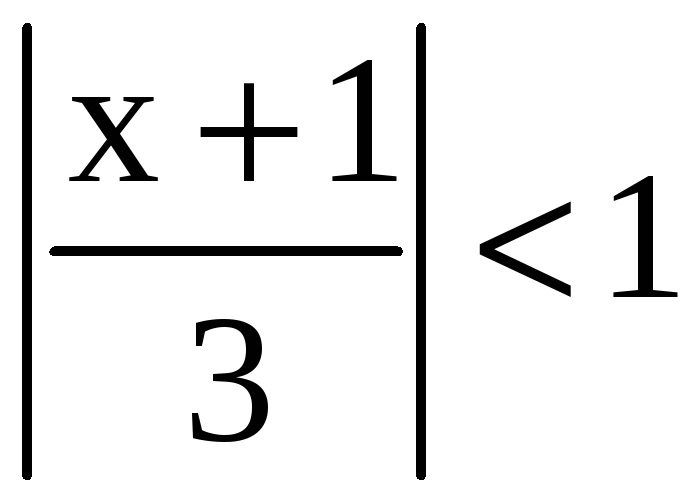 и
и
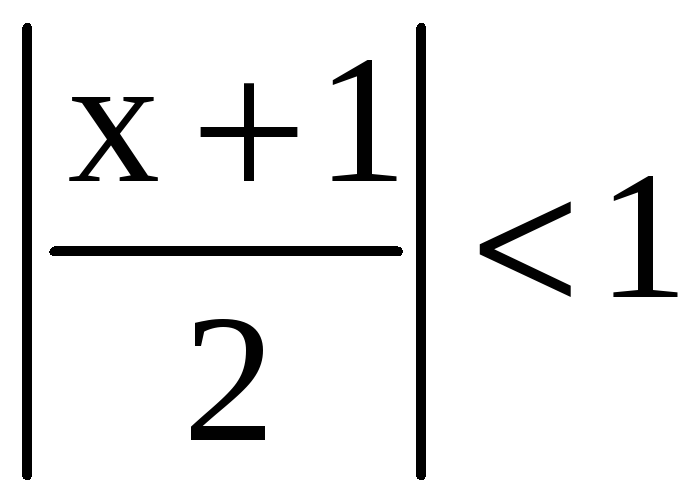 .
Это пересечение даёт
.
Это пересечение даёт
![]() .
.
Пример 15. Найти первые четыре ненулевые члена разложения решения дифференциального уравнения в степенной ряд
![]()
![]() ,
, ![]() .
.
Решение. Будем предполагать, что неизвестная функция, являющаяся решением дифференциального уравнения, представима степенным рядом
 ,
(11)
,
(11)
коэффициенты
которого определяются путём
последовательного дифференцирования
исходного уравнения
![]() и подстановкой в него
и подстановкой в него
![]() и найденных позже значений
и найденных позже значений
![]() .
Итак, имеем:
.
Итак, имеем:
![]() ,
,
![]() ,
, ![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Осталось подставить найденные значения в ряд (11):
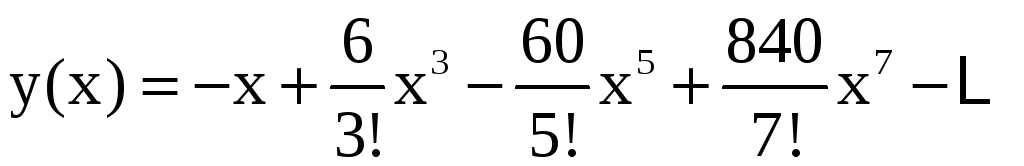 ,
,
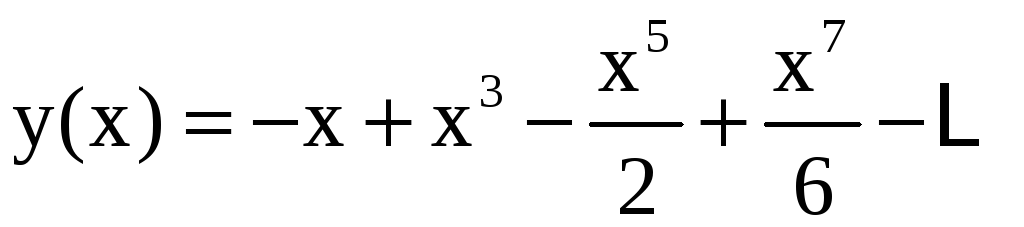 .
.
