
XI. Ряды
1. Числовые ряды. Сходимость числового ряда Числовым рядом называется выражение вида
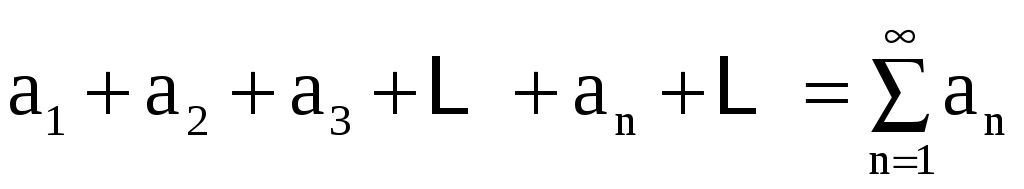 , (1)
, (1)
в
котором слагаемые
![]() – числа, называемые членами ряда.
– числа, называемые членами ряда.
Сумма
n
первых членов ряда
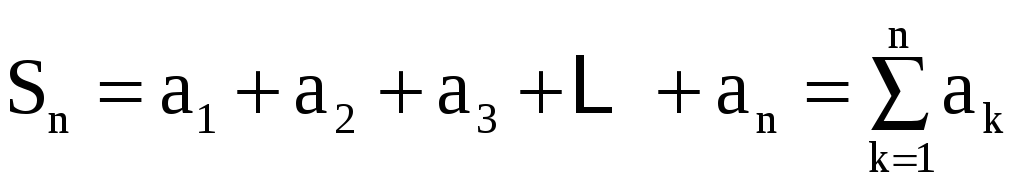 называется n-й
частичной суммой ряда. Если существует
конечный предел
называется n-й
частичной суммой ряда. Если существует
конечный предел
![]() ,
то числовой ряд (1) называется сходящимся,
а число S
– суммой ряда; в противном случае
числовой ряд называется расходящимся.
Ряд
,
то числовой ряд (1) называется сходящимся,
а число S
– суммой ряда; в противном случае
числовой ряд называется расходящимся.
Ряд
 называется n-м
остатком ряда; ряд (1) сходится, если его
n-е
остатки сходятся и их суммы стремятся
к нулю.
называется n-м
остатком ряда; ряд (1) сходится, если его
n-е
остатки сходятся и их суммы стремятся
к нулю.
Пример 1. Доказать сходимость рядов:
a)
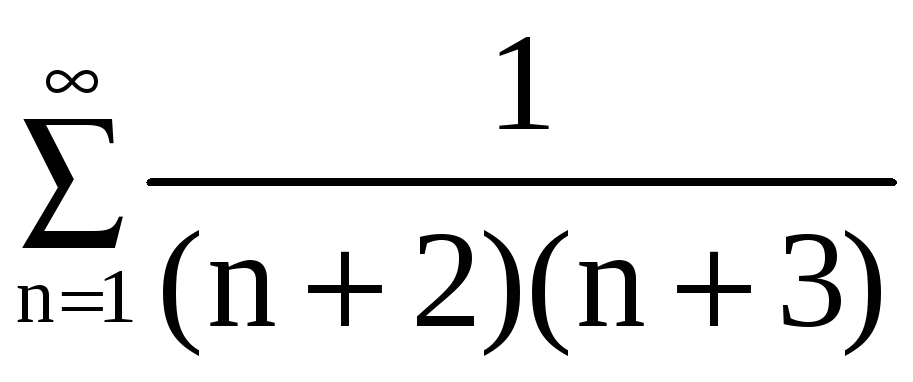 ;
б)
;
б)
![]() ,
,
![]() .
.
Решение.
а) Общий член
ряда
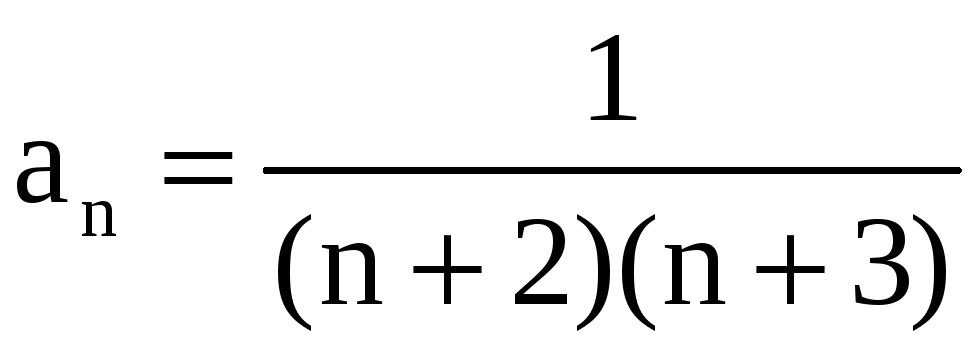 .
и так далее. Эту дробь можно представить
в виде суммы двух простых дробей
.
и так далее. Эту дробь можно представить
в виде суммы двух простых дробей
 .
.
Поэтому
n-ю
частичную сумму
![]() ряда можно записать следующим образом:
ряда можно записать следующим образом:
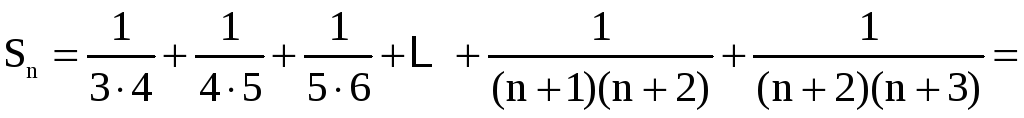
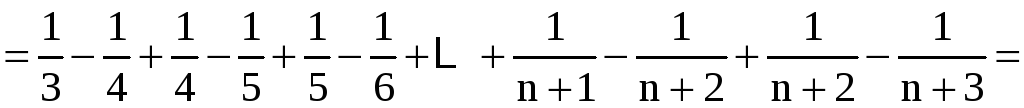
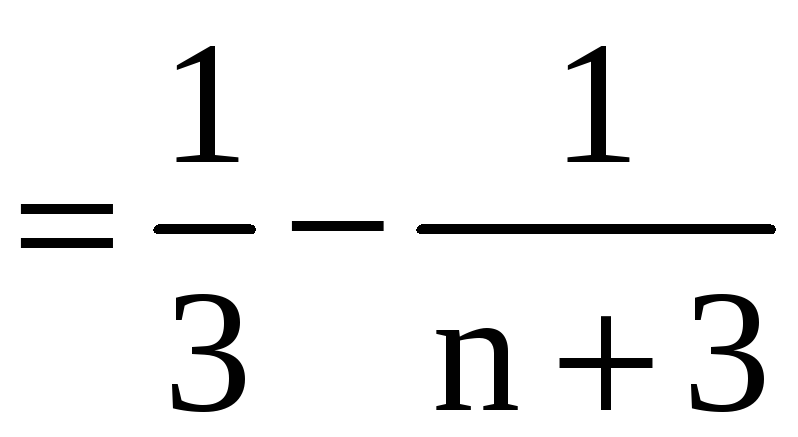 .
.
Имеем
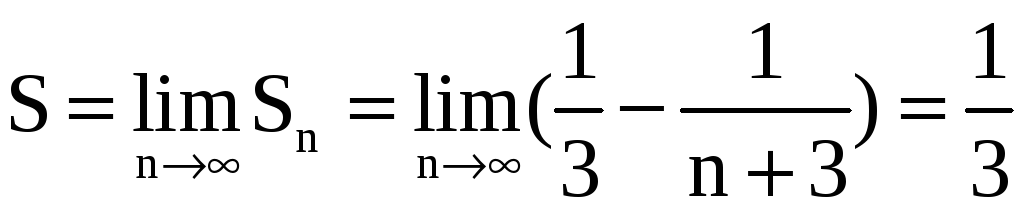 .
Таким образом, наш числовой ряд сходится
к сумме
.
Таким образом, наш числовой ряд сходится
к сумме
![]() .
.
б)
Члены числового ряда
![]() образуют геометрическую прогрессию с
первым (нулевым) членом
образуют геометрическую прогрессию с
первым (нулевым) членом
![]() и знаменателем q.
При
и знаменателем q.
При
![]() прогрессия является убывающей, и ряд
сходится к
прогрессия является убывающей, и ряд
сходится к
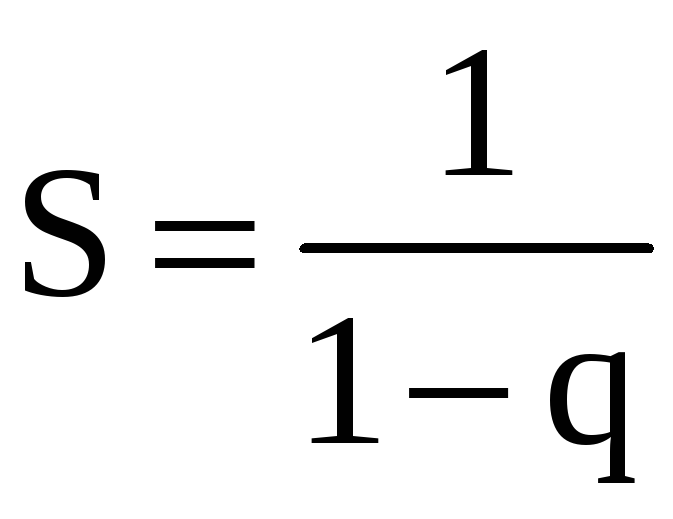 .
.
Критерий Коши.
Для сходимости числового ряда (1)
необходимо и достаточно, чтобы для
любого
![]() существовало натуральное число
существовало натуральное число
![]() такое,
что для любых n
> N
и m
> 0 справедливо неравенство
такое,
что для любых n
> N
и m
> 0 справедливо неравенство
![]() . (2)
. (2)
Пример 2.
Доказать
расходимость гармонического ряда
![]() .
.
Решение.
Зададимся
![]() и
и
![]() и найдём номер N,
такой что для любого
и найдём номер N,
такой что для любого
![]()
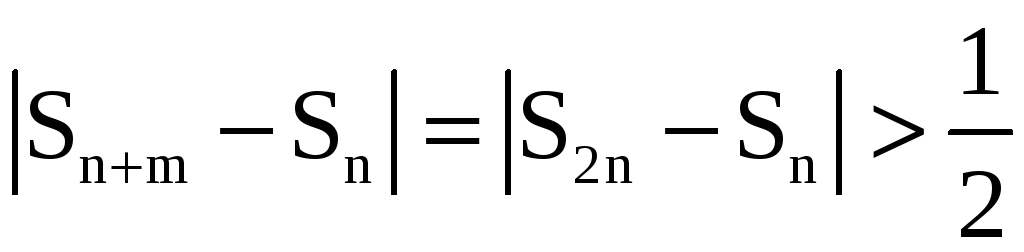 .
.
Имеем
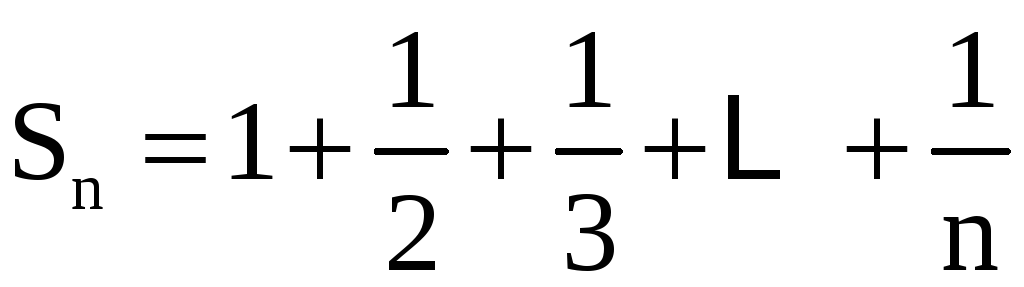 ,
,
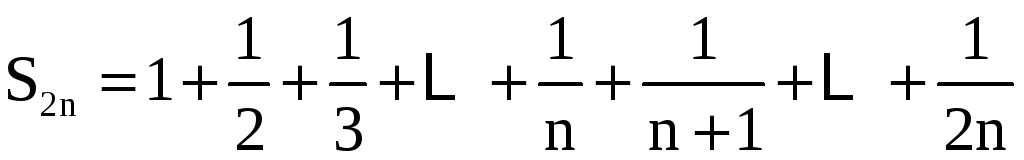 ,
,
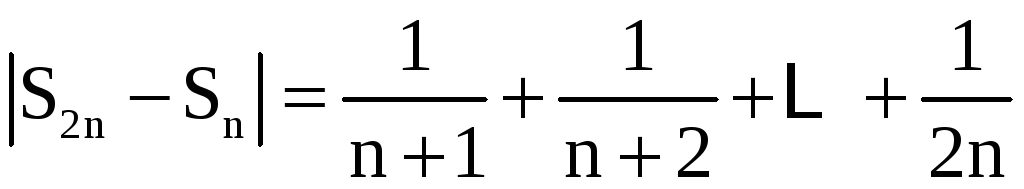 .
.
В
последней сумме n
слагаемых и наименьшее из них равно
![]() .
Если каждое из слагаемых заменить на
меньшее, то сумма уменьшится, поэтому
.
Если каждое из слагаемых заменить на
меньшее, то сумма уменьшится, поэтому
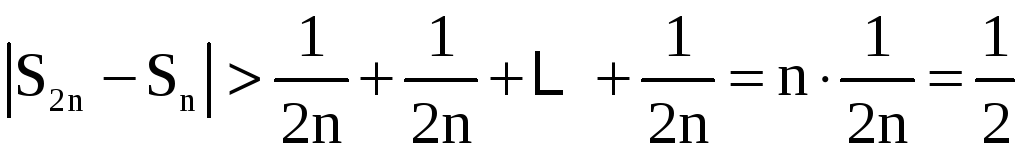 .
.
Как
видим,
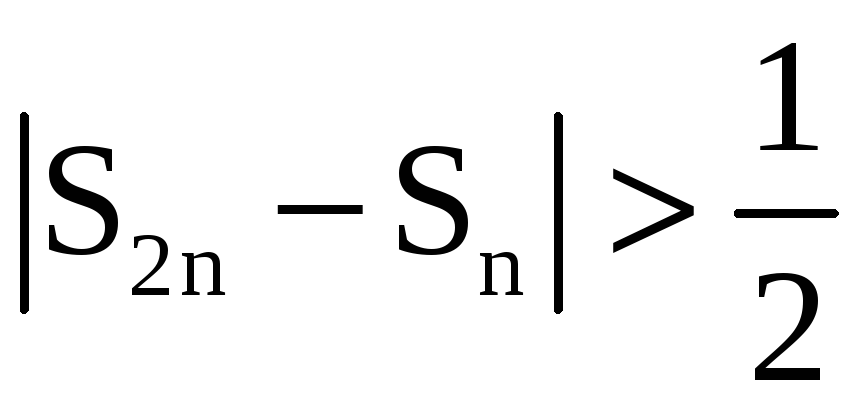 для любого n
и не выполняется условие критерия Коши,
следовательно, ряд расходится.
для любого n
и не выполняется условие критерия Коши,
следовательно, ряд расходится.
Необходимое
условие сходимости.
Если
числовой ряд (1) сходится, то
![]() .
.
Пример 3.
Доказать
расходимость ряда
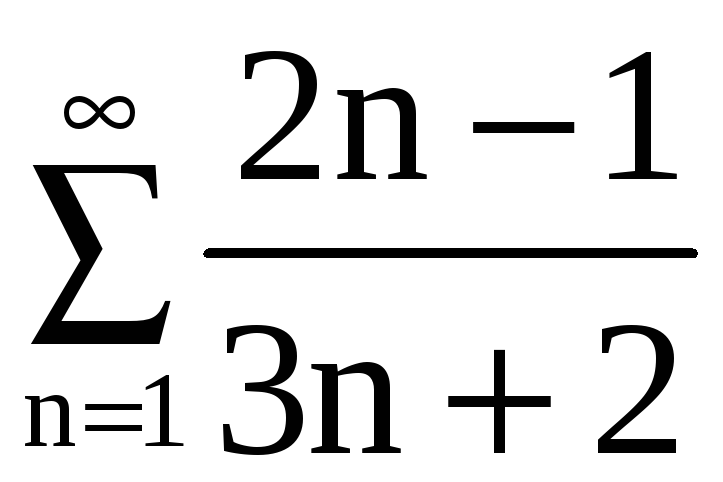 .
.
Решение.
Проверим выполнение необходимого
условия сходимости. Имеем
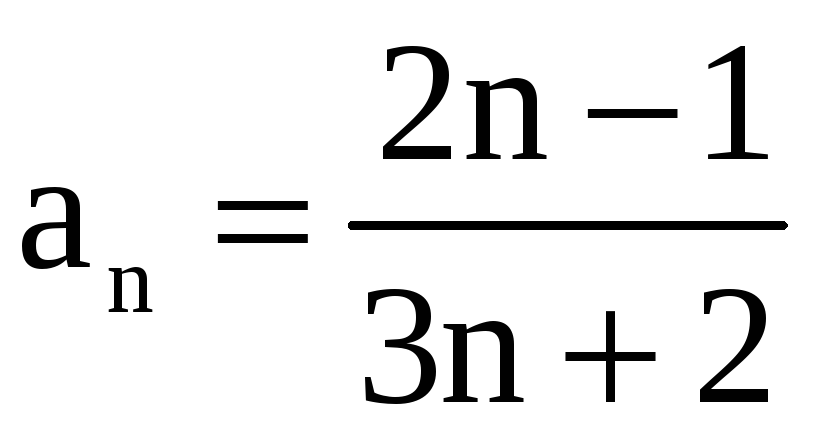 ,
,
 .
.
Так
как
![]() ,
то ряд расходится.
,
то ряд расходится.
Отметим,
что необходимое условие сходимости (![]() )
не является достаточным для сходимости
ряда (пример 2).
)
не является достаточным для сходимости
ряда (пример 2).
2. Признаки сходимости числовых рядов
Теорема 1 (первый
признак сравнения). Пусть
наряду с рядом (1) дан числовой ряд
![]() и пусть
и пусть
![]() для любого
для любого
![]() .
Тогда:
.
Тогда:
![]() если ряд
если ряд
![]() сходится, то ряд (1) также сходится;
сходится, то ряд (1) также сходится;
![]() если ряд
если ряд
![]() расходится, то ряд
расходится, то ряд
![]() также расходится.
также расходится.
Теорема 2 (второй
признак сравнения). Пусть
наряду с рядом (1) дан числовой ряд
![]() (
(![]() )
и пусть существует предел
)
и пусть существует предел
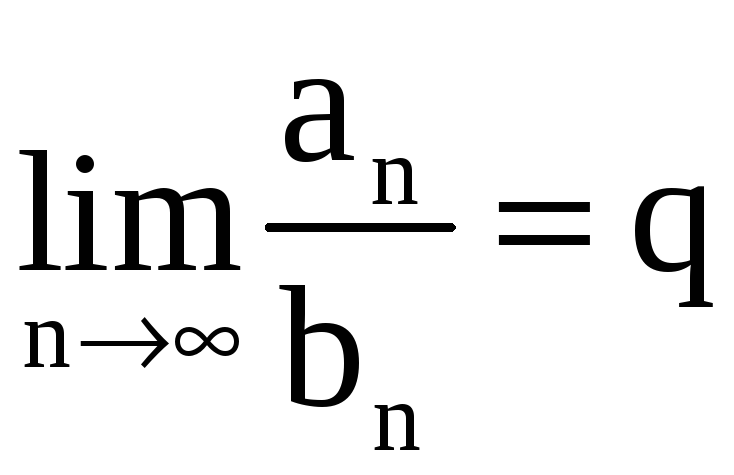 ,
при этом
,
при этом
![]() .
Тогда ряды
.
Тогда ряды
![]() и
и
![]() ведут себя одинаково в смысле сходимости
(то есть или одновременно сходятся, или
одновременно расходятся).
ведут себя одинаково в смысле сходимости
(то есть или одновременно сходятся, или
одновременно расходятся).
Часто при исследовании на сходимость ряда используется тот хорошо известный факт, что ряд

Пример 4.
Исследовать на сходимость ряды: а) 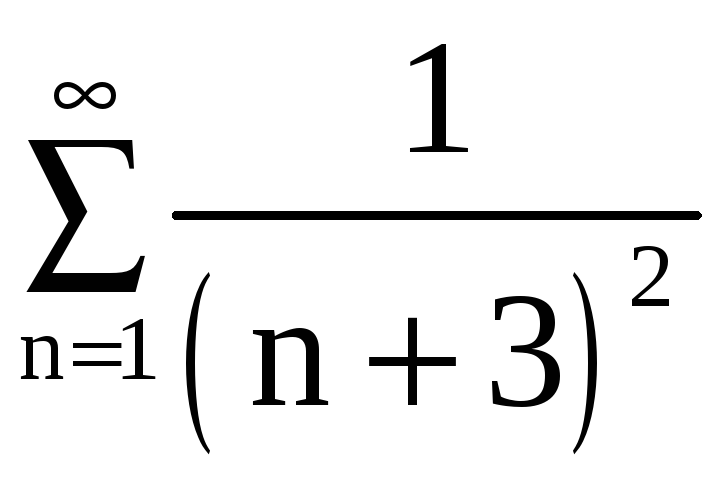 ,
б)
,
б) 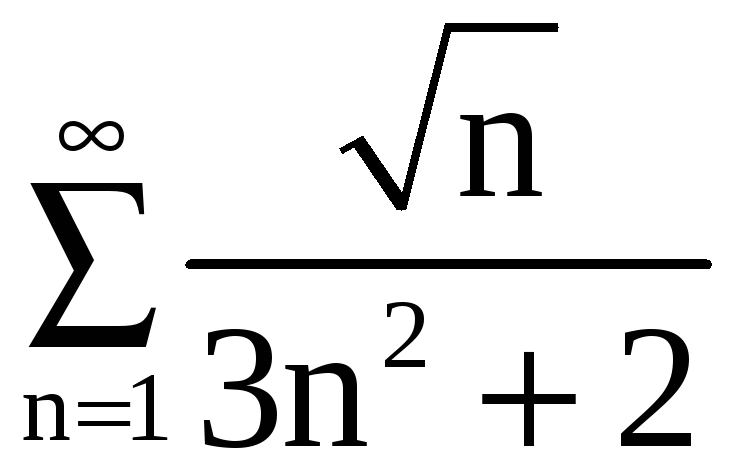 , в)
, в)
 , г)
, г)
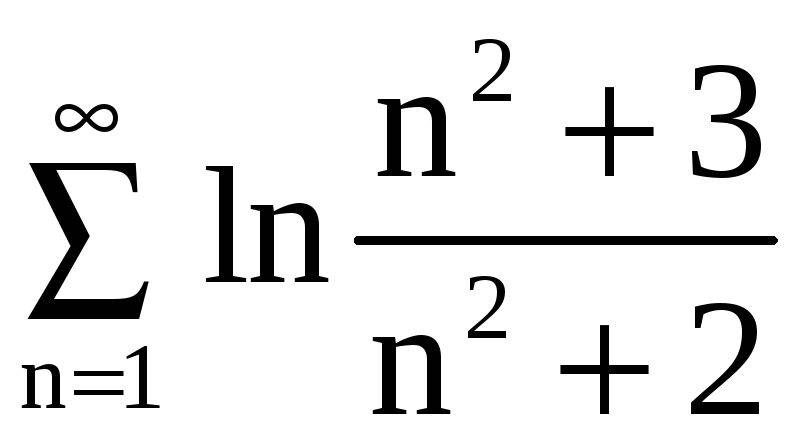 , д)
, д)
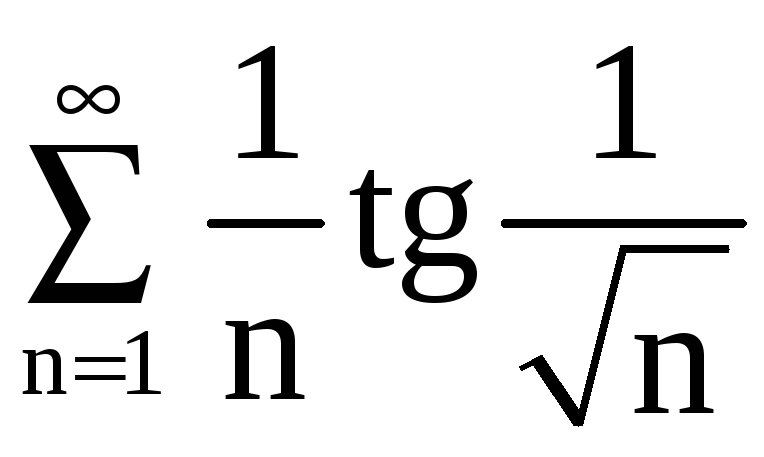 ,
,
е)
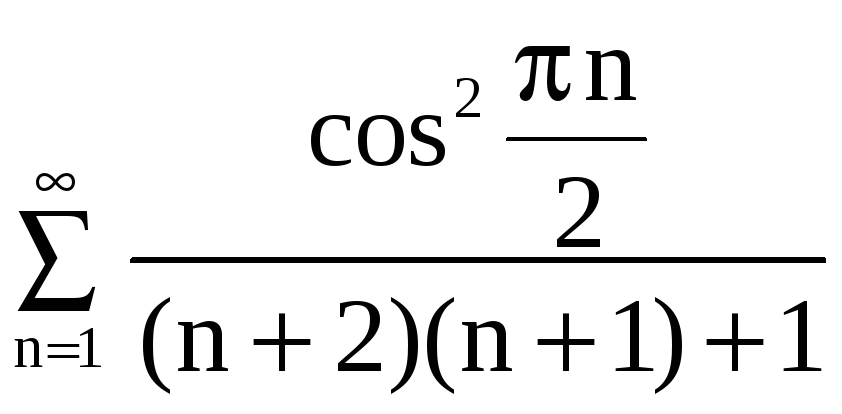 .
.
Решение.
а) В качестве вспомогательного ряда
![]() возьмём числовой ряд
возьмём числовой ряд
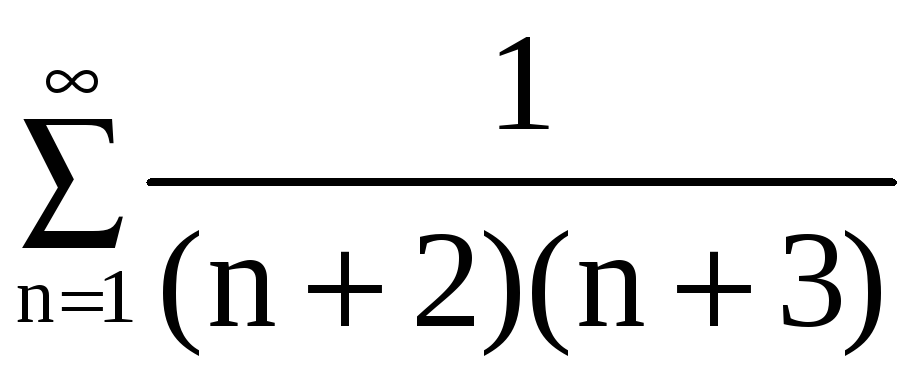 ,
сходимость которого доказана в примере
1 (а). Имеем
,
сходимость которого доказана в примере
1 (а). Имеем
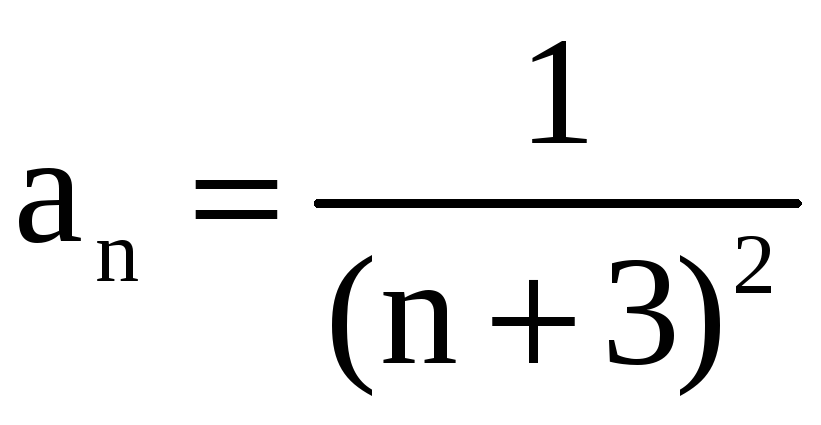 ,
,
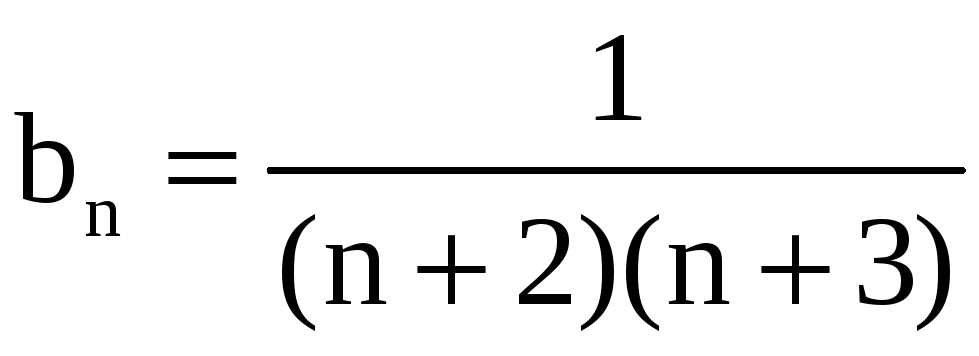 ,
,
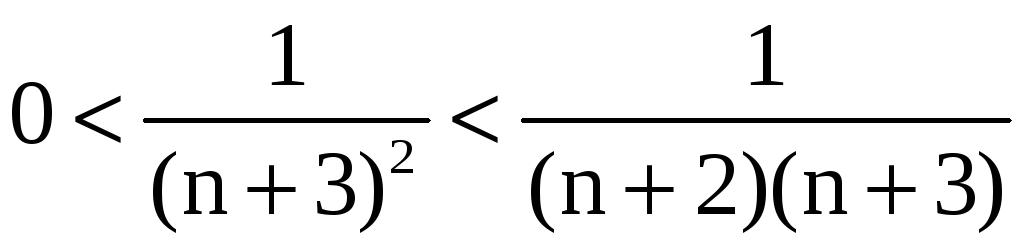 для любого n
.
для любого n
.
Согласно первому
признаку сравнения, сходимость ряда
![]() влечёт за собой сходимость нашего ряда
влечёт за собой сходимость нашего ряда
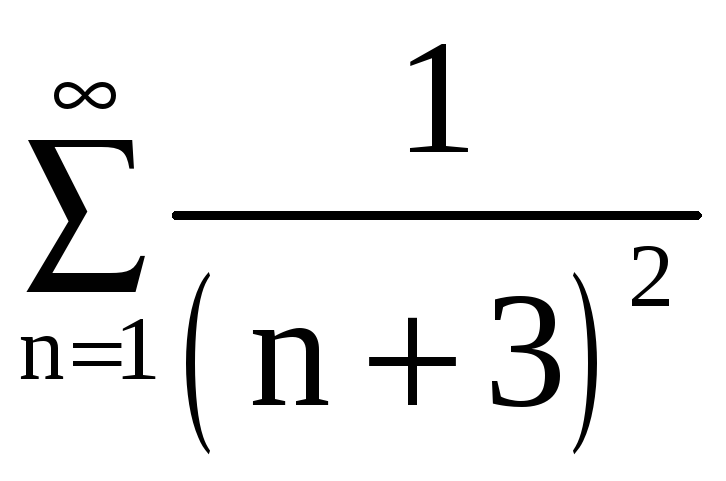 .
.
б) В качестве
вспомогательного ряда возьмём ряд
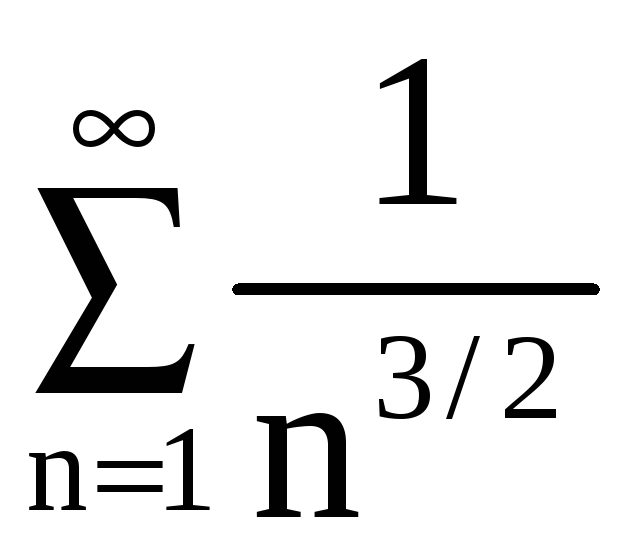 .Имеем
.Имеем
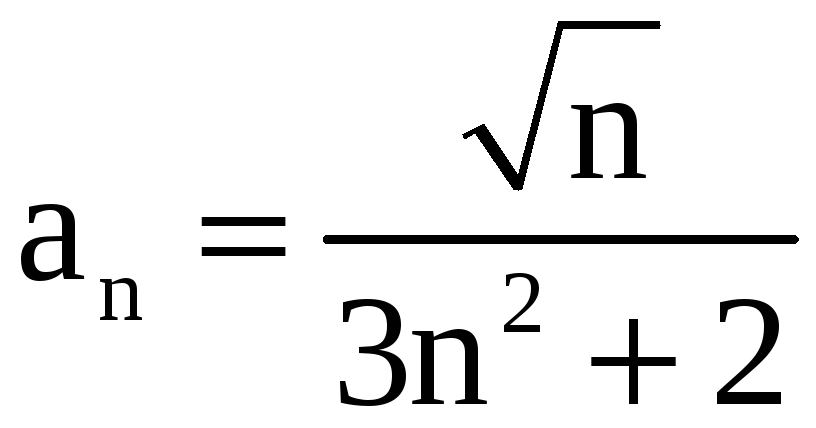 ,
,
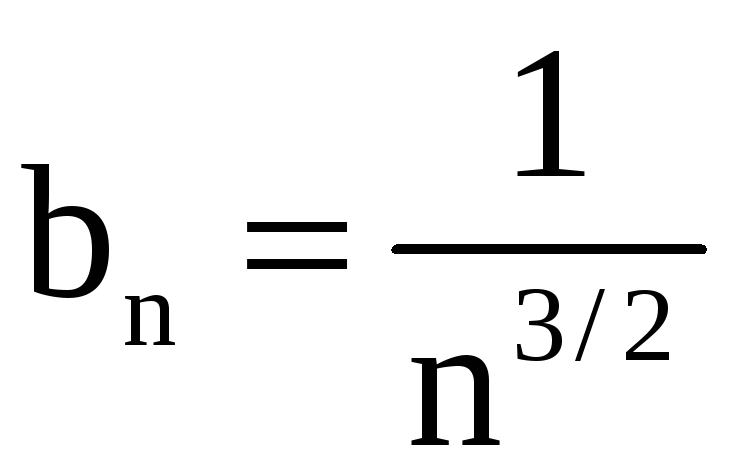 ,
,
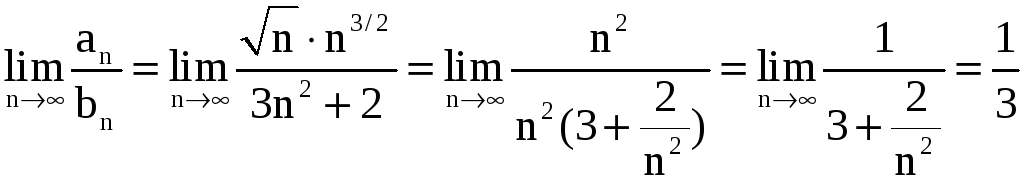 .
.
Так как
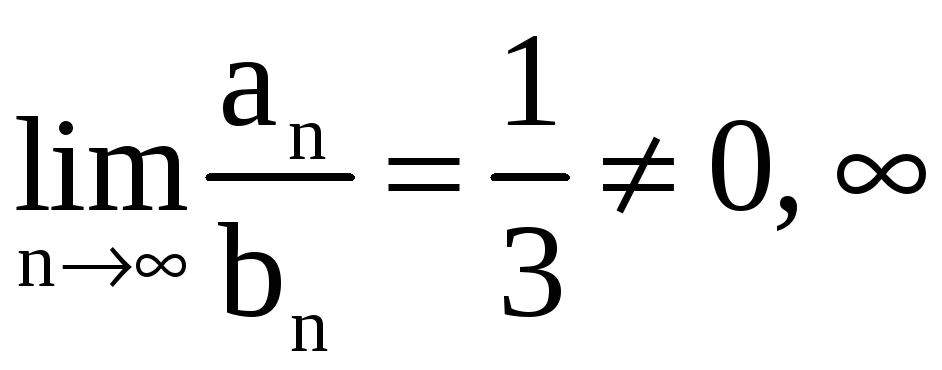 ,
то ряды
,
то ряды
![]() ,
,
![]() ведут себя одинаково в смысле сходимости.
Но ряд
ведут себя одинаково в смысле сходимости.
Но ряд
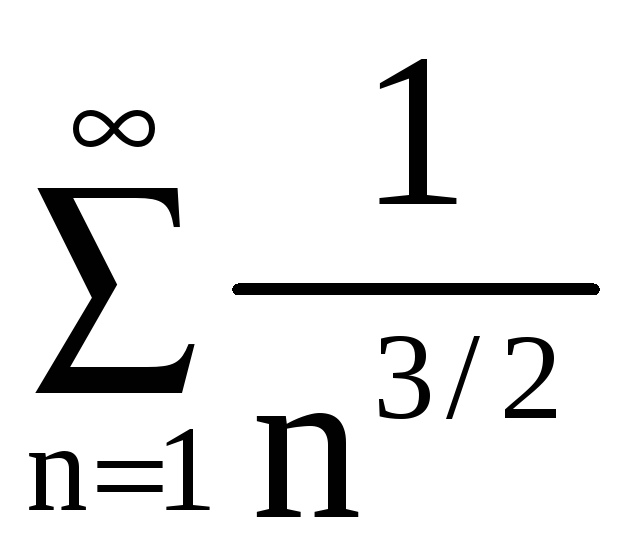 сходится
сходится
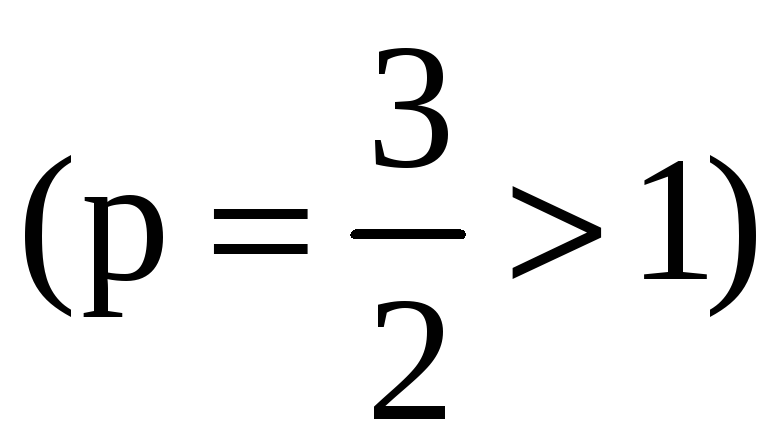 ,
следовательно, сходится и наш ряд.
,
следовательно, сходится и наш ряд.
в) В качестве
вспомогательного ряда возьмём
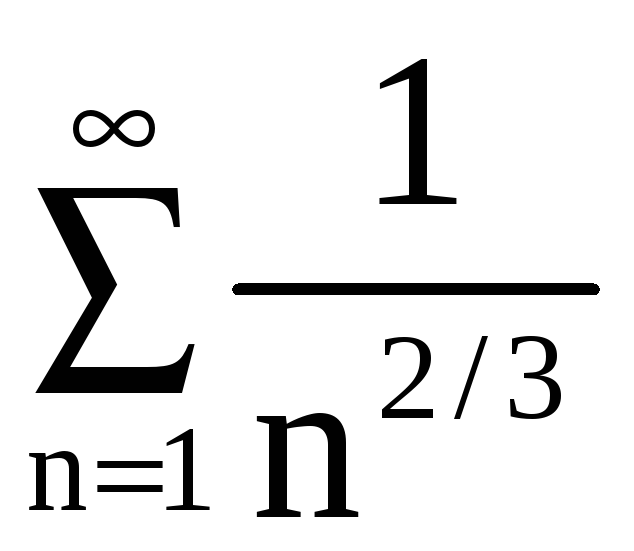 .
Имеем
.
Имеем
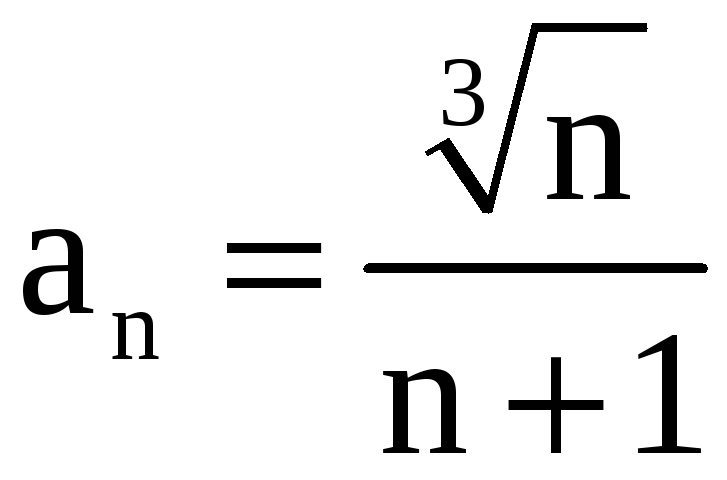 ,
,
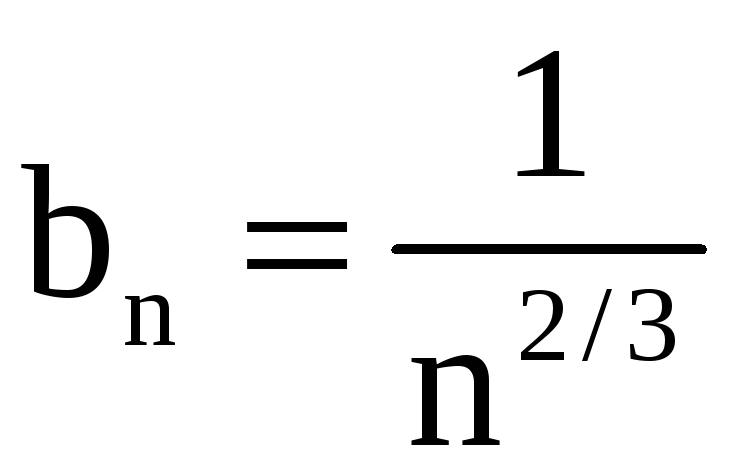 ,
,
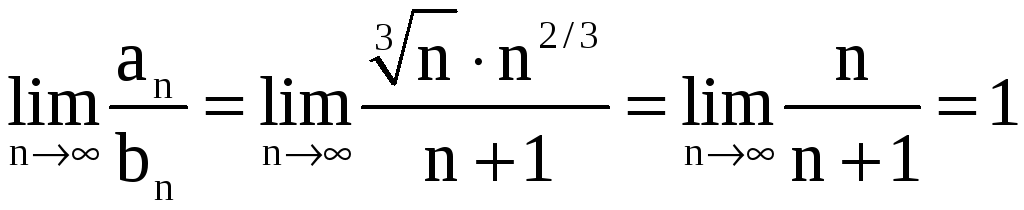 .
.
Так как
 ,
то ряды
,
то ряды
![]() и
и
![]() ведут себя одинаково в смысле сходимости.
Ряд
ведут себя одинаково в смысле сходимости.
Ряд
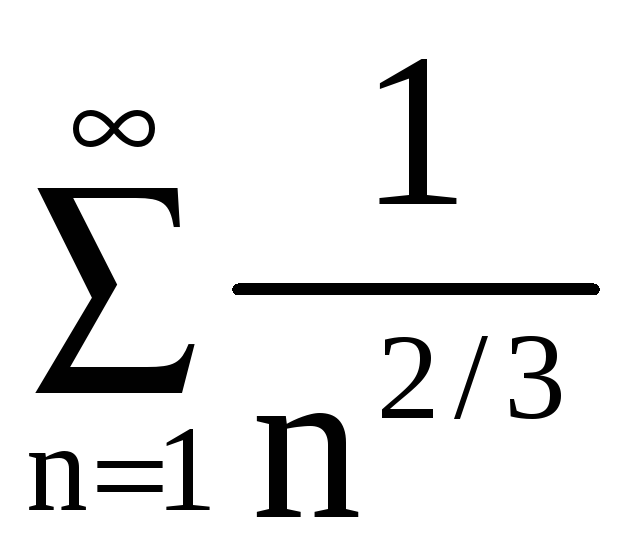 расходится
расходится
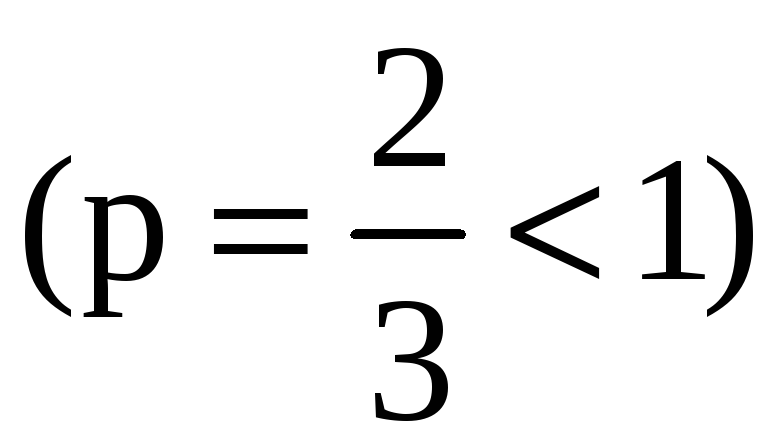 ,
следовательно, наш ряд
,
следовательно, наш ряд
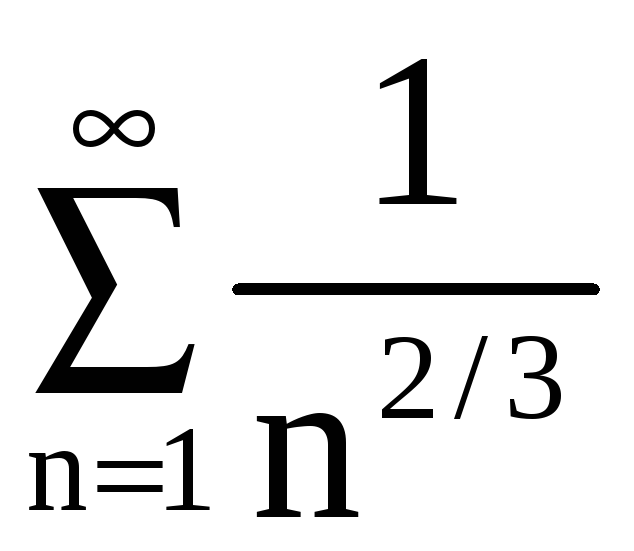 расходится.
расходится.
г)
Для сравнения возьмём ряд
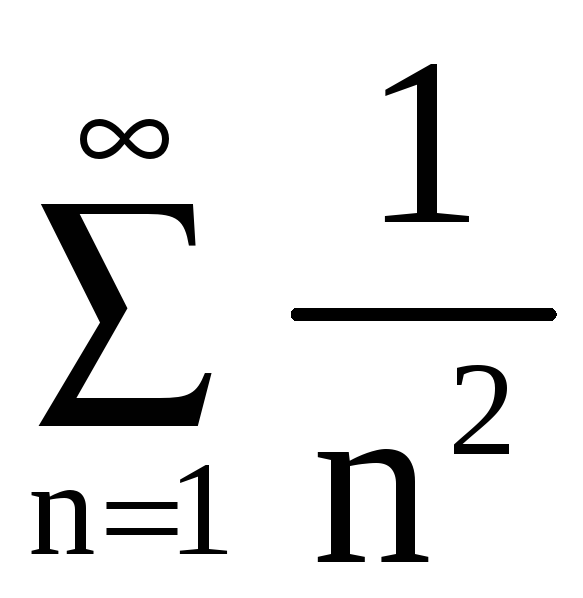 .
Так как это ряд вида
.
Так как это ряд вида
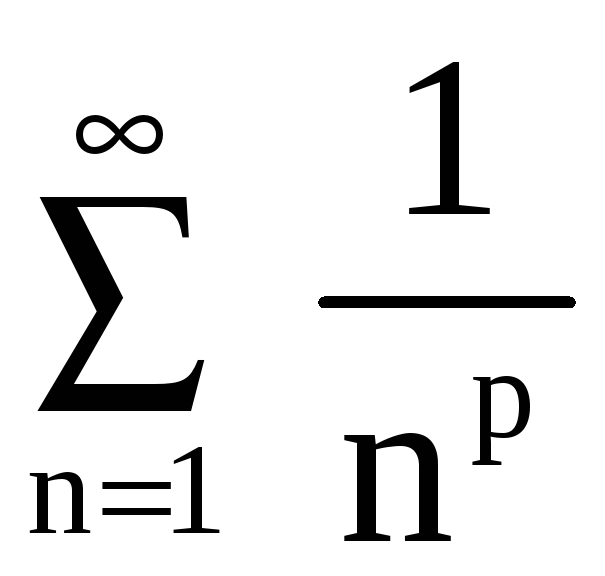 ,
где
,
где
![]() ,
то он сходится.
,
то он сходится.
Применим предельный признак сравнения:
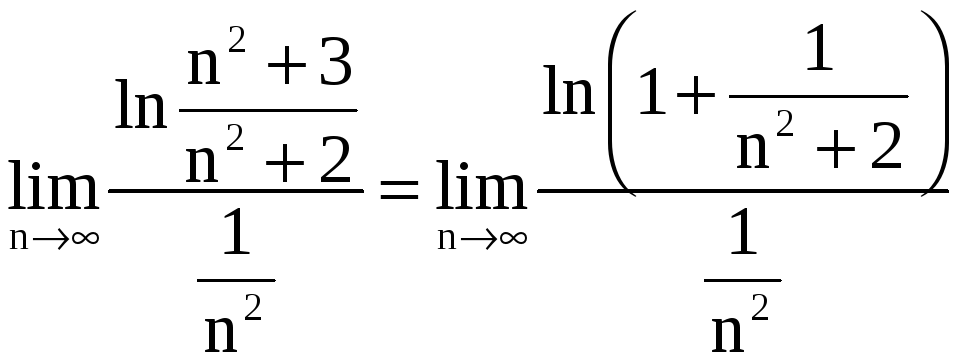 .
.
При
![]()
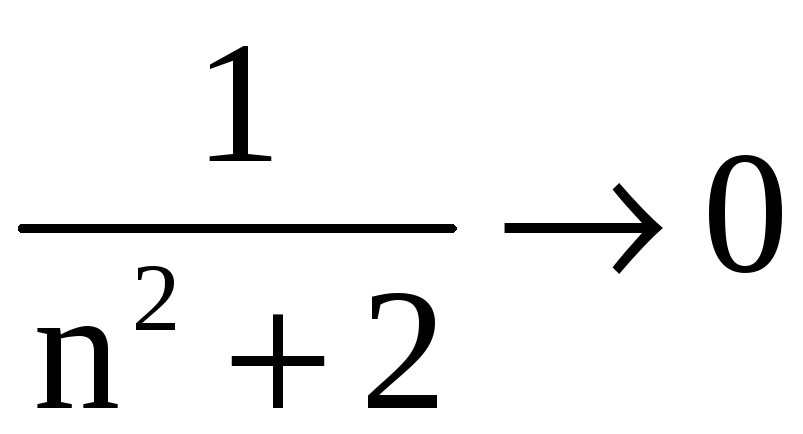 и величина
и величина
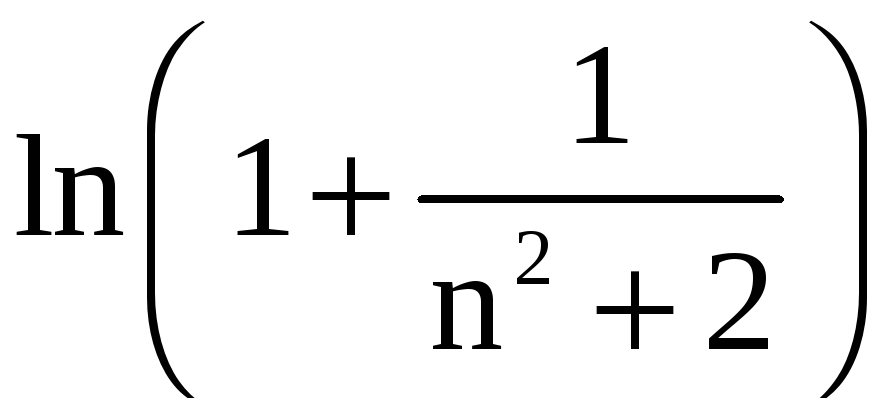 эквивалентна
эквивалентна
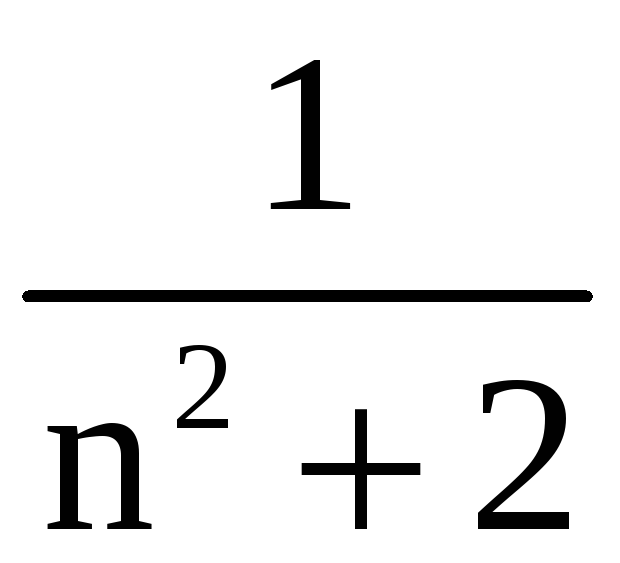 .
.
Поэтому
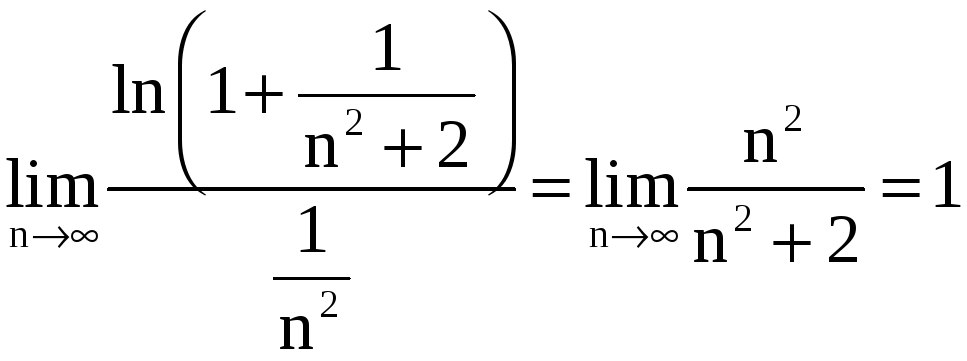 .
.
Так
как ряд
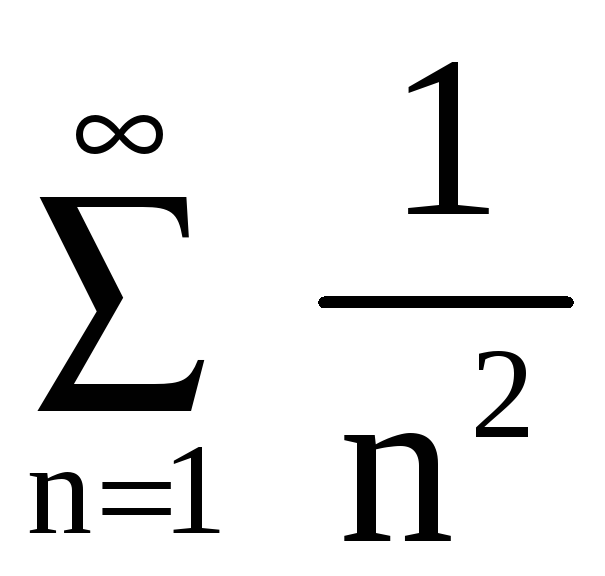 сходится, то и данный ряд сходится.
сходится, то и данный ряд сходится.
д)
При
![]() бесконечно малая величина
бесконечно малая величина
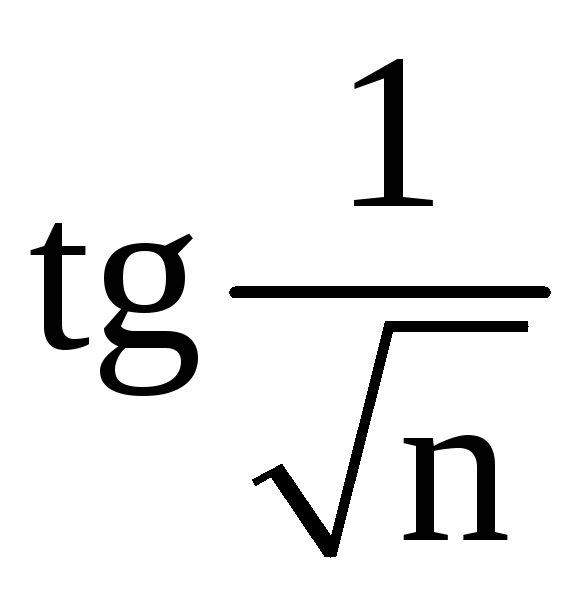 эквивалентна
эквивалентна
![]() .
Поэтому для сравнения возьмём ряд
.
Поэтому для сравнения возьмём ряд
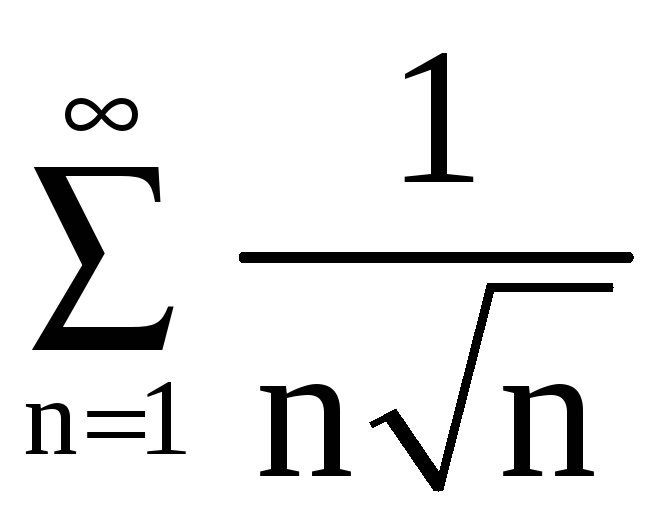 .
Этот ряд вида
.
Этот ряд вида
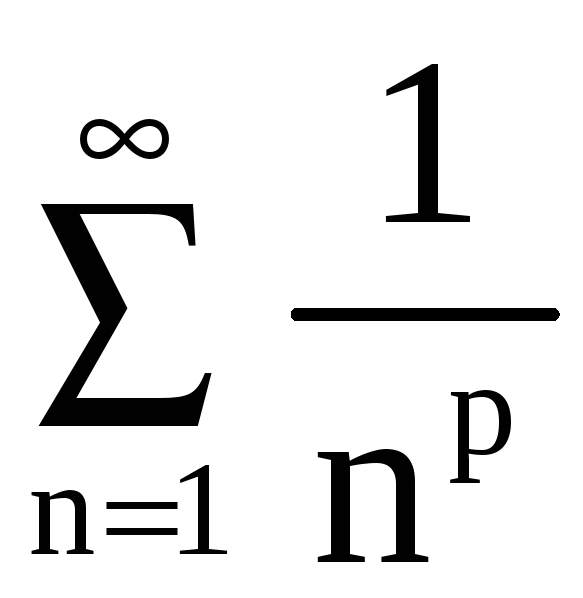 ,
где
,
где
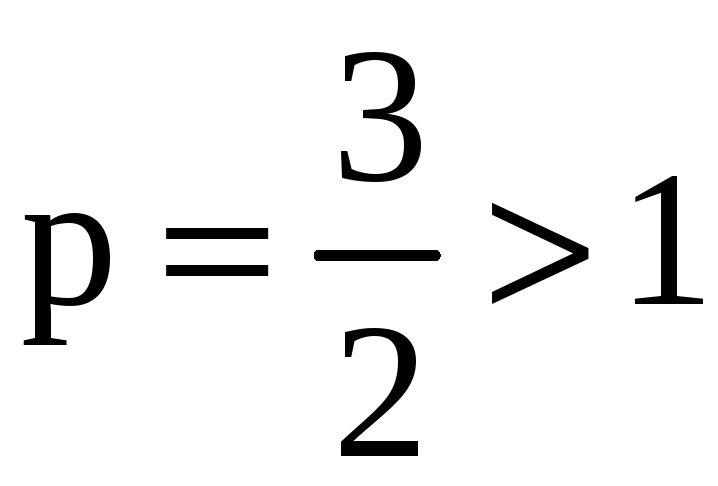 .
Следовательно, ряд
.
Следовательно, ряд
 сходится.
сходится.
Применим предельный признак сравнения:
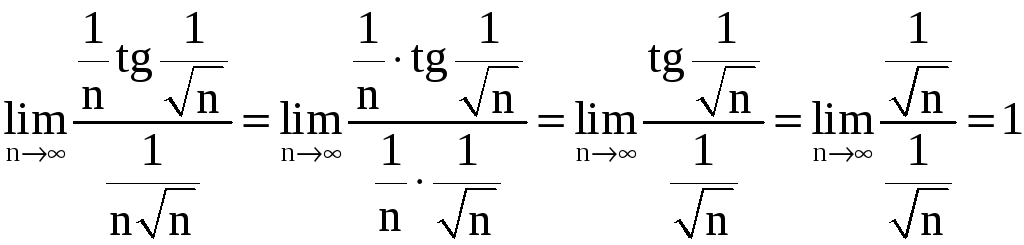 .
.
Так
как ряд
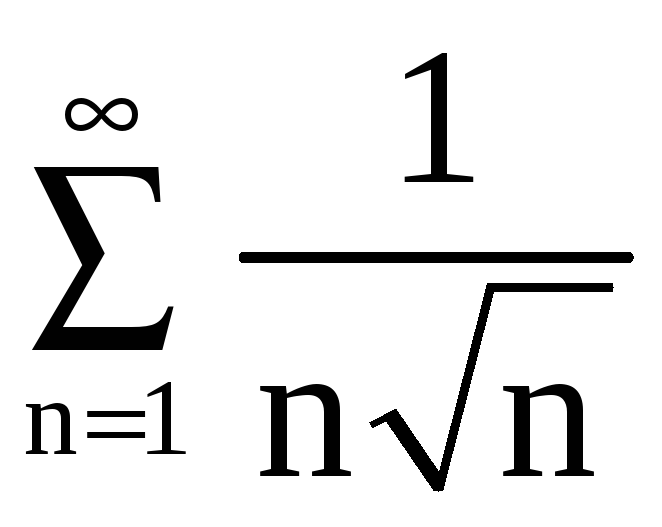 сходится, то и данный ряд сходится.
сходится, то и данный ряд сходится.
е) В
качестве вспомогательного ряда возьмём
ряд
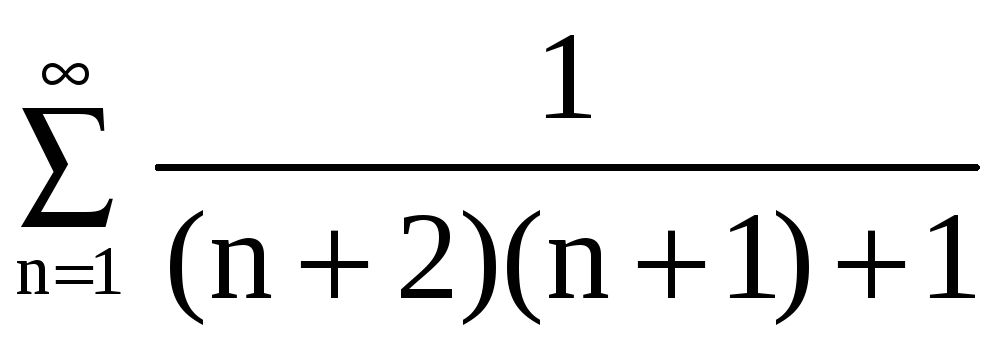 .
.
Сравним
его со сходящимся рядом
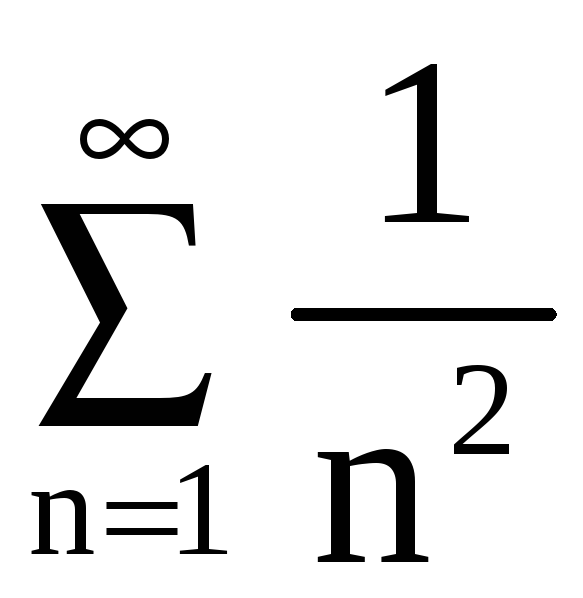 по предельному признаку сравнения.
по предельному признаку сравнения.
Поскольку
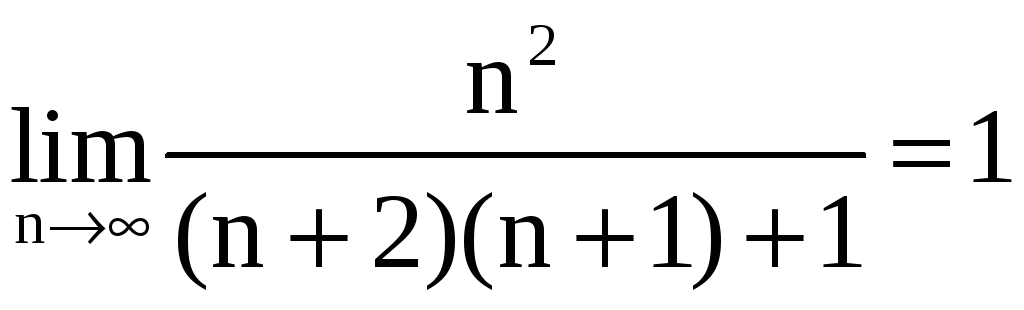 ,
а ряд
,
а ряд
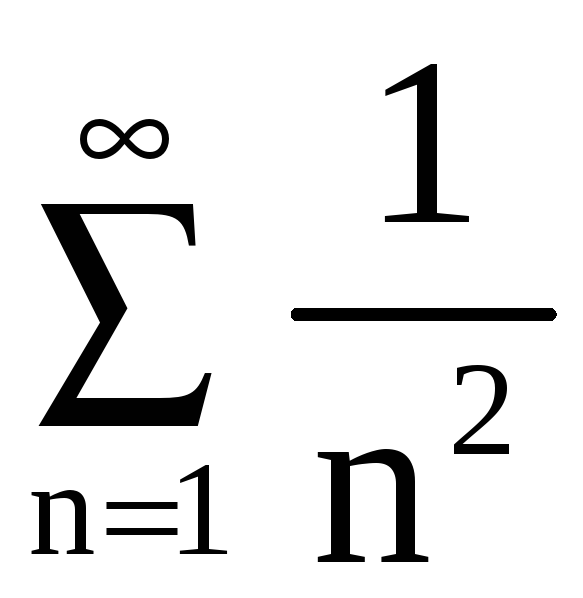 сходится, то и ряд
сходится, то и ряд
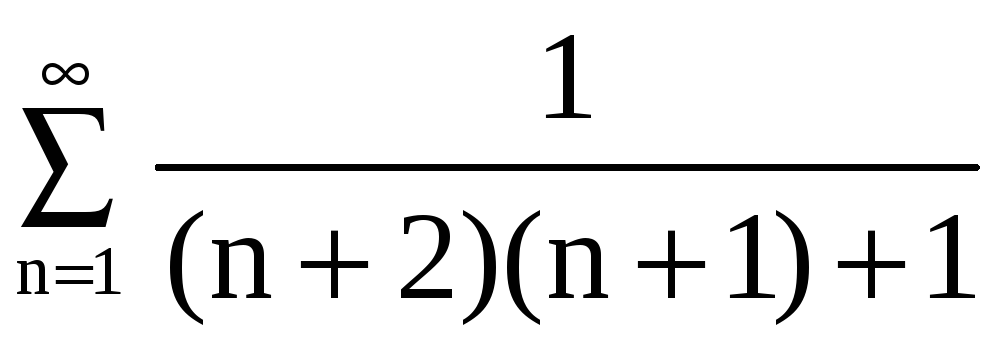 сходящийся.
сходящийся.
Так
как
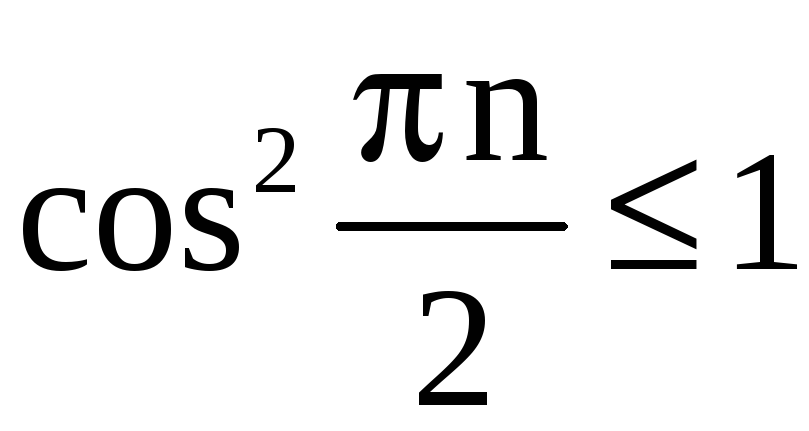 ,
то
,
то
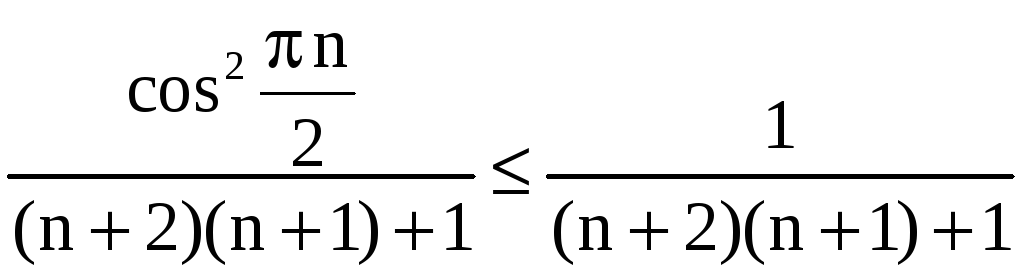 .
Следовательно, по признаку сравнения
исходный ряд сходится.
.
Следовательно, по признаку сравнения
исходный ряд сходится.
Теорема 3. Если изменить конечное число членов ряда, то это не скажется на сходимости (расходимости) ряда.
Отсюда
следует, что теорема 1 справедлива и в
том случае, если неравенство
![]() выполняется, начиная с некоторого номера
n.
выполняется, начиная с некоторого номера
n.
Теорема 4
(признак сходимости Даламбера). Если
члены числового ряда (1) положительны и
существует предел
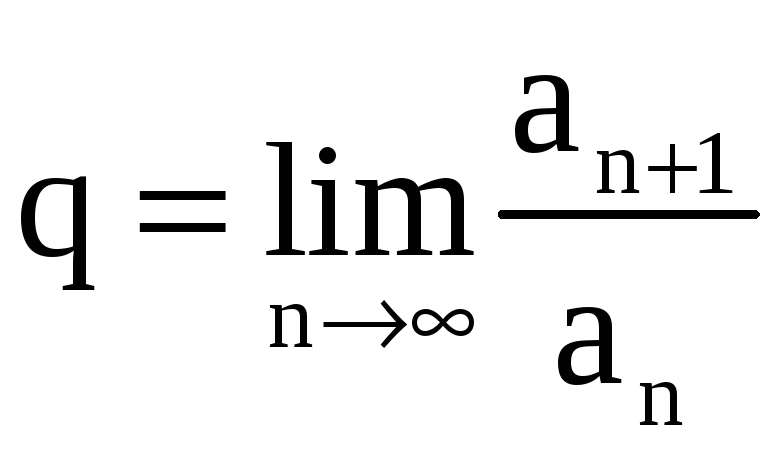 ,
то:
,
то:
![]() при
при
![]() ряд (1) сходится;
ряд (1) сходится;
![]() при
при
![]() ряд (1) расходится.
ряд (1) расходится.
Пример
5. Исследовать
на сходимость числовые ряды: а)![]() ,
б)
,
б)![]() , в)
, в)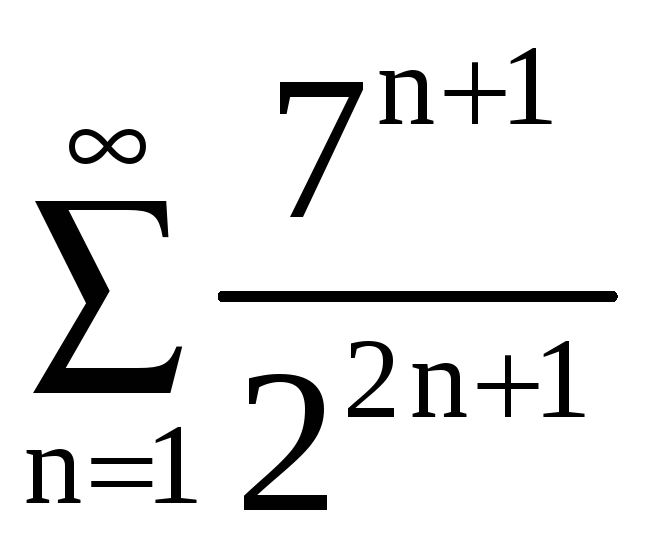 .
.
Решение. а) Имеем 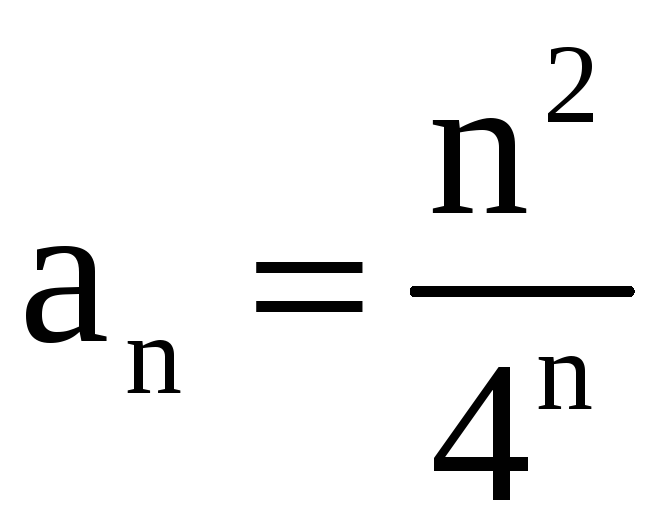 ,
, 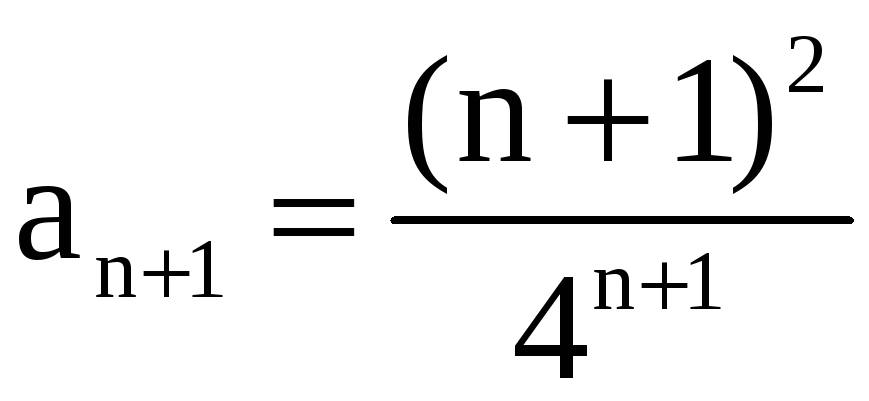 ,
,
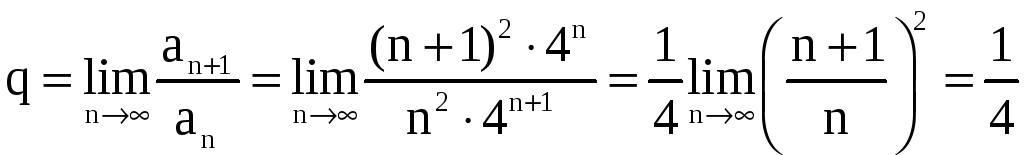 .
.
Так как
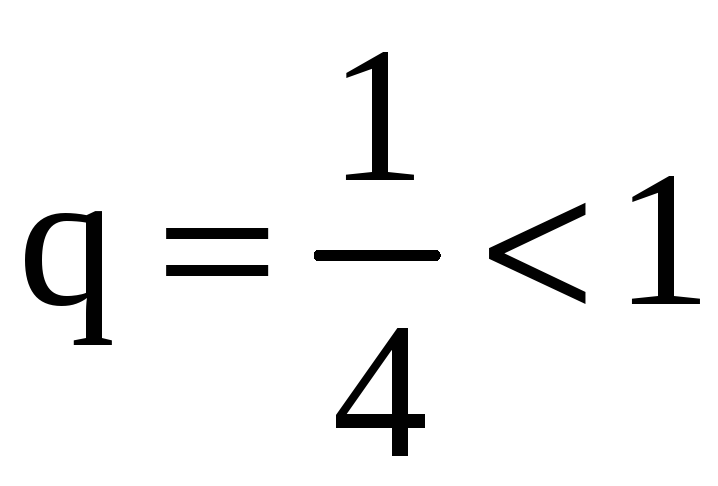 ,
то согласно признаку Даламбера ряд
сходится.
,
то согласно признаку Даламбера ряд
сходится.
б) В данном случае
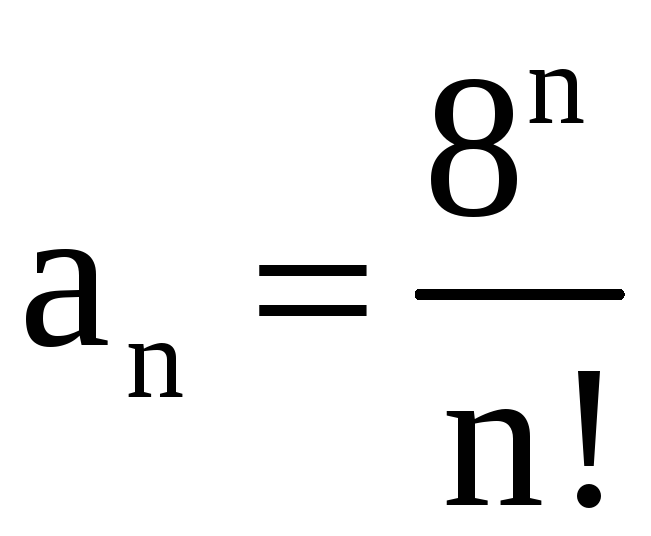 ,
,
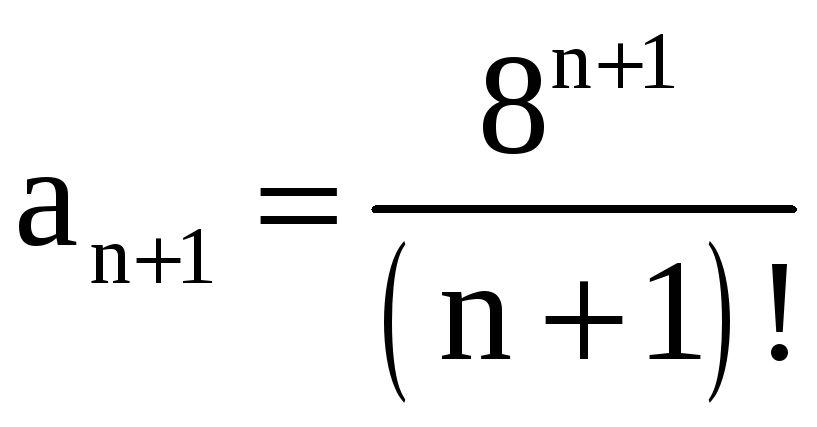 ,
,
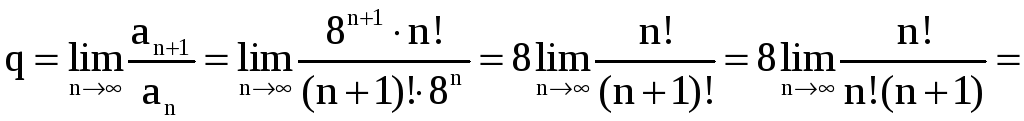
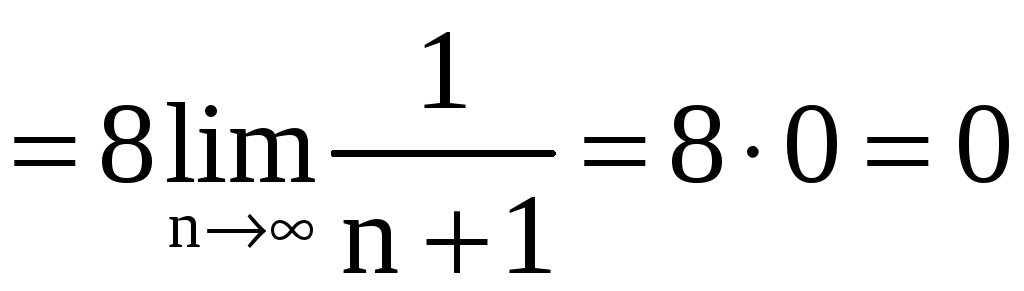 .
.
Так как
![]() ,
то ряд сходится.
,
то ряд сходится.
в) Имеем
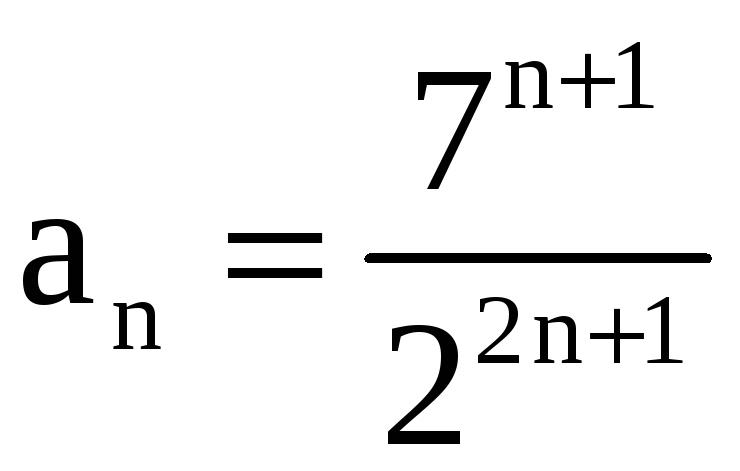 ,
,
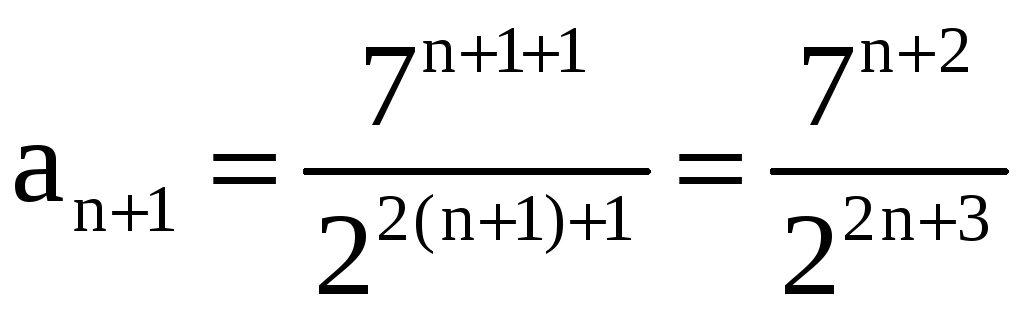 ,
,
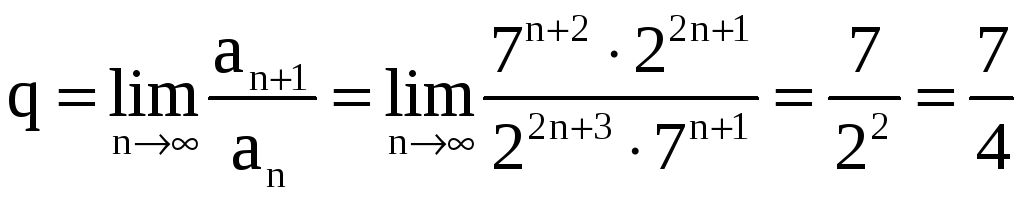 .
.
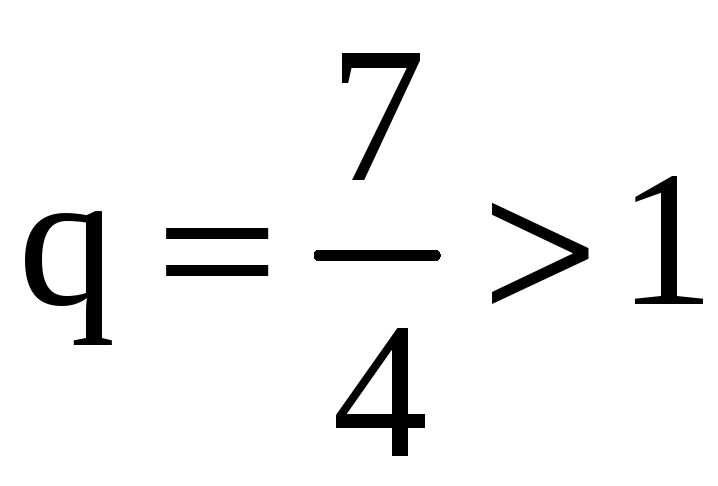 ,
следовательно, ряд расходится.
,
следовательно, ряд расходится.
Теорема
5 (радикальный признак Коши). Если
члены числового ряда (1) неотрицательны
и существует предел
![]() ,
то:
,
то:
![]() при
q
< 1 ряд сходится;
при
q
< 1 ряд сходится;
![]() при
q
> 1 ряд расходится.
при
q
> 1 ряд расходится.
Пример 6. Исследовать
на сходимость числовые ряды: а)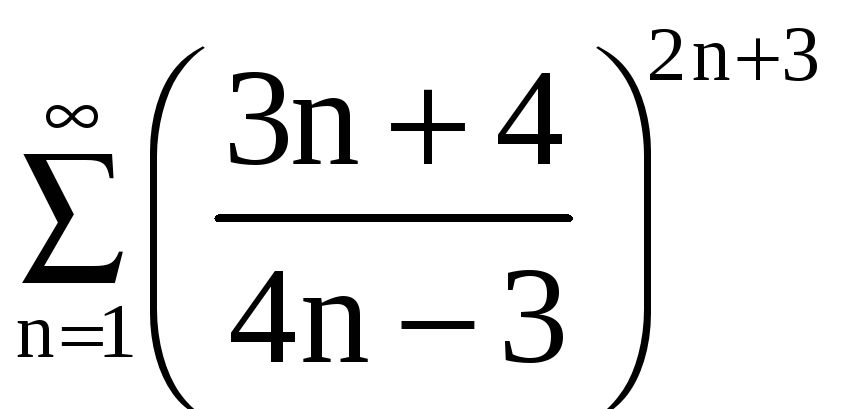 ,
б)
,
б)
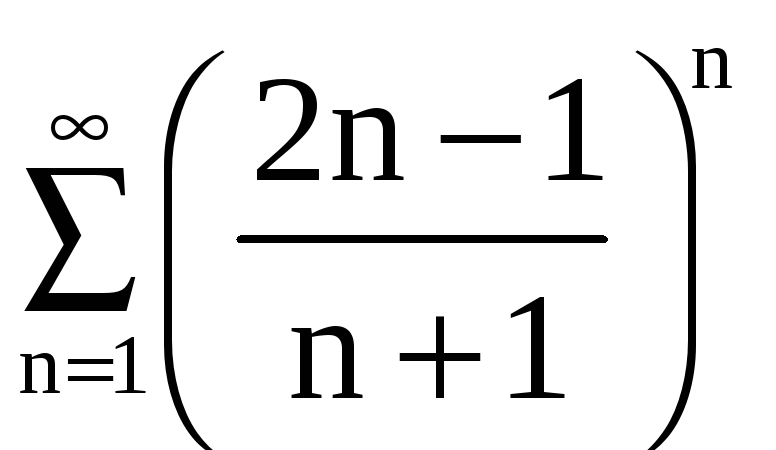 , в)
, в)
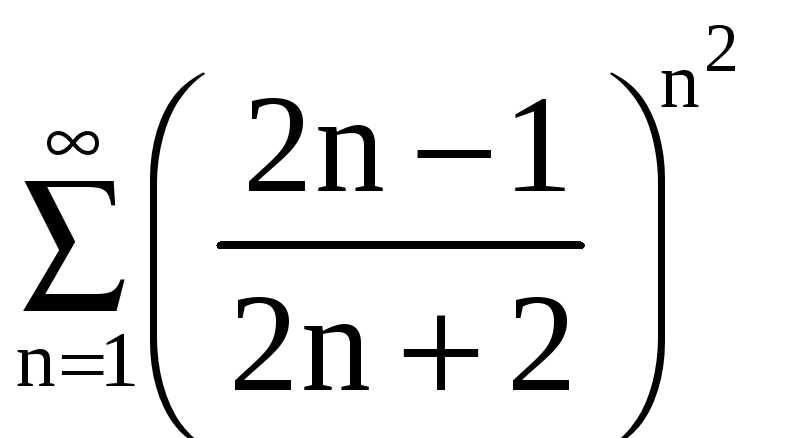 .
.
Решение.
а) Имеем
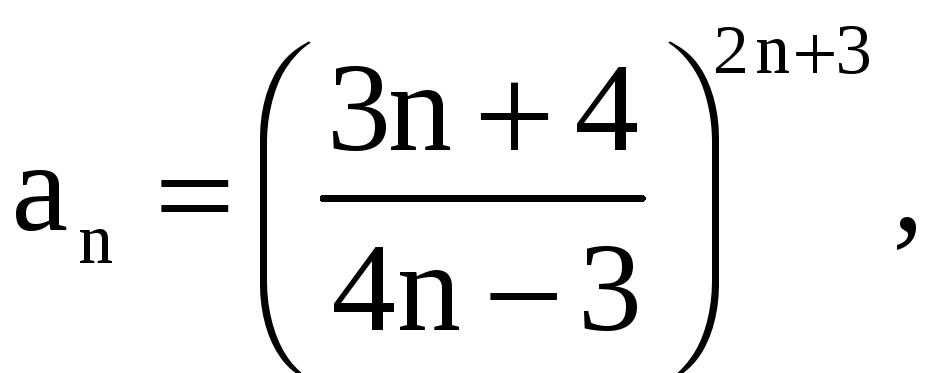
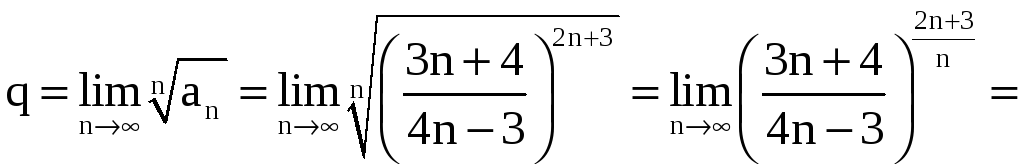
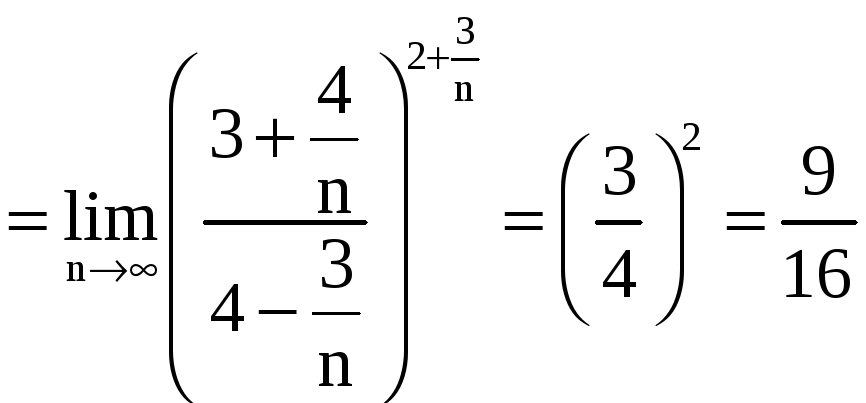 .
.
Так как q = 9/16 < 1, то согласно радикальному признаку Коши ряд сходится.
б)
Имеем
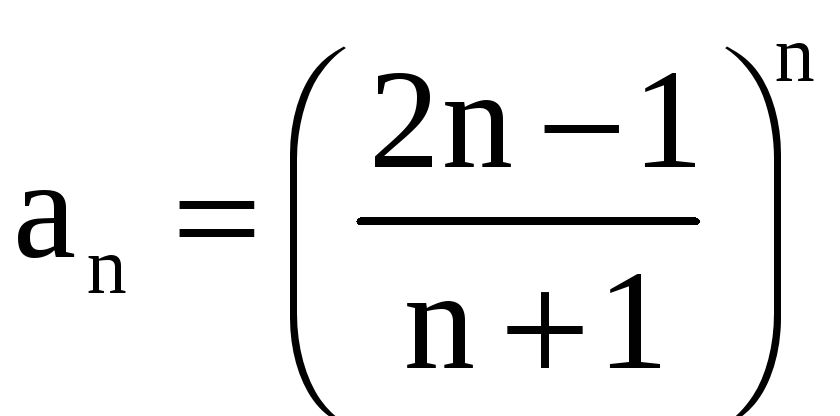 ,
,
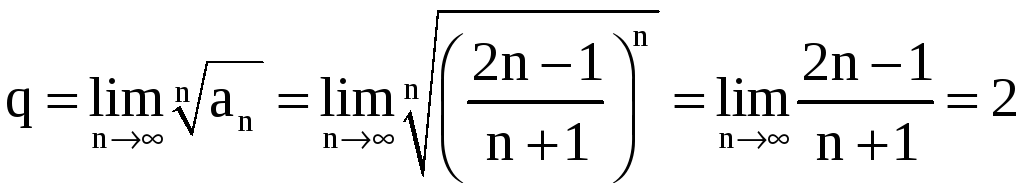 .
.
Этот ряд расходится, так как q = 2 > 1.
в)
В этом случае
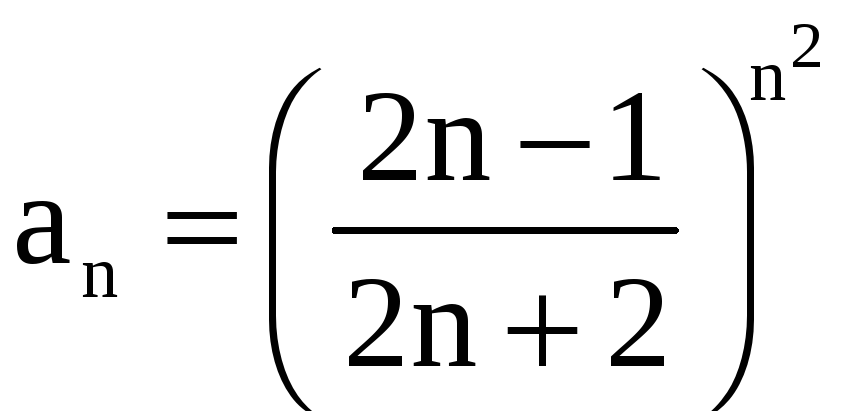 ,
,
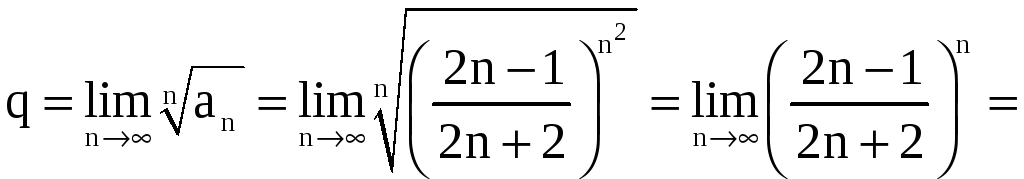
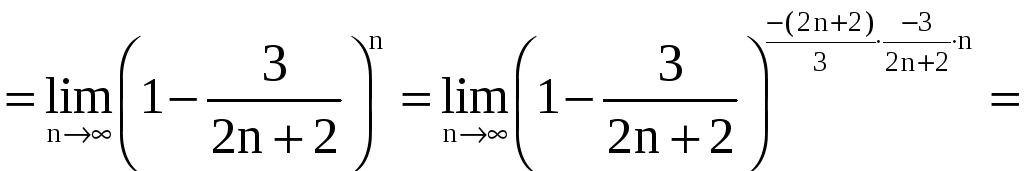
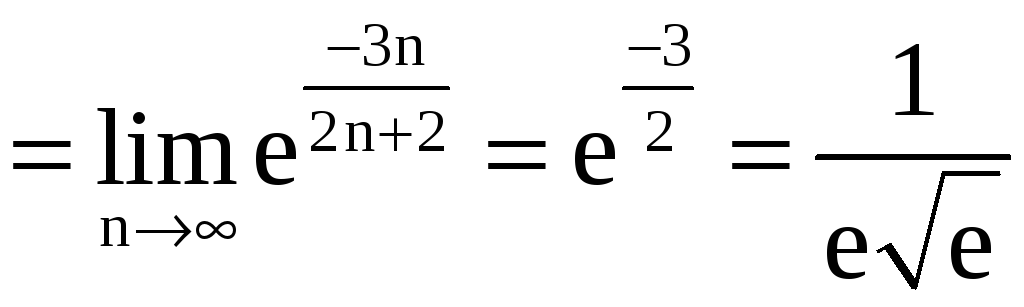 .
.
Так
как
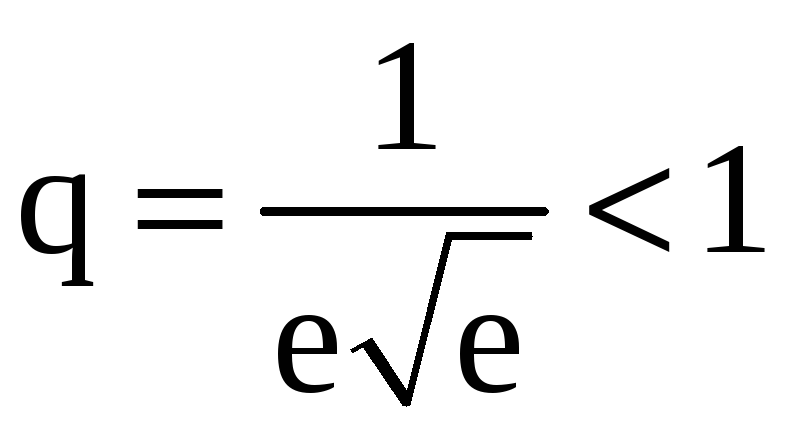 ,
то этот ряд сходится.
,
то этот ряд сходится.
Теорема
6 (интегральный признак Коши). Пусть
функция f(x)
определена на [1; + )
и является невозрастающей неотрицательной
функцией. Пусть
![]() для любого n.
Тогда числовой ряд (1) и несобственный
интеграл
для любого n.
Тогда числовой ряд (1) и несобственный
интеграл
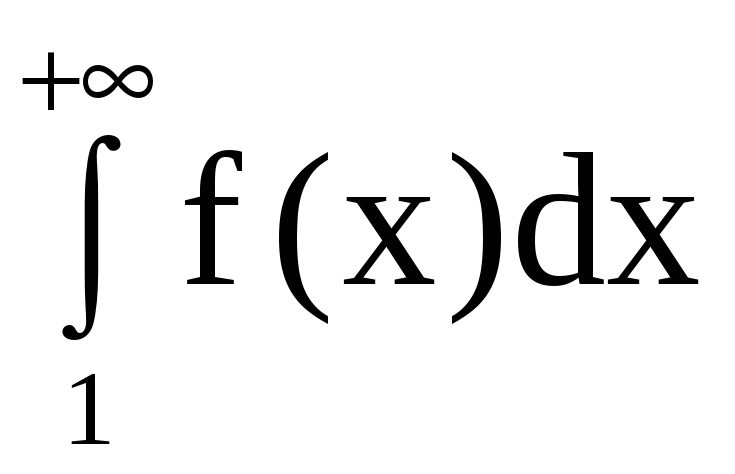 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7. Исследовать на сходимость числовые ряды:
а)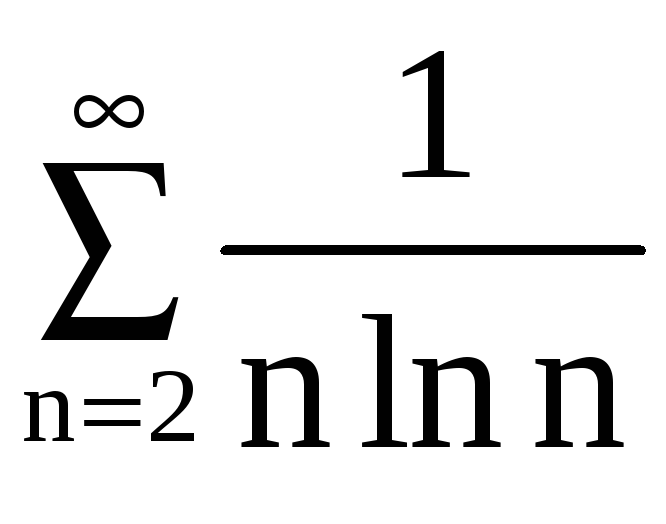 ,
б)
,
б)
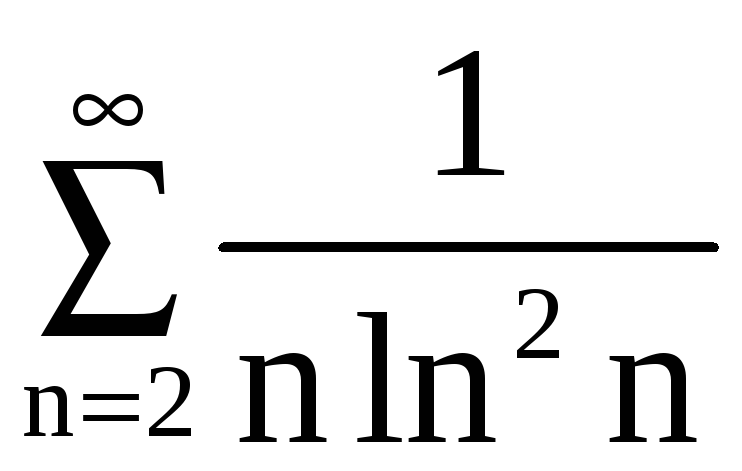 .
.
Решение.
а) Введём в
рассмотрение функцию
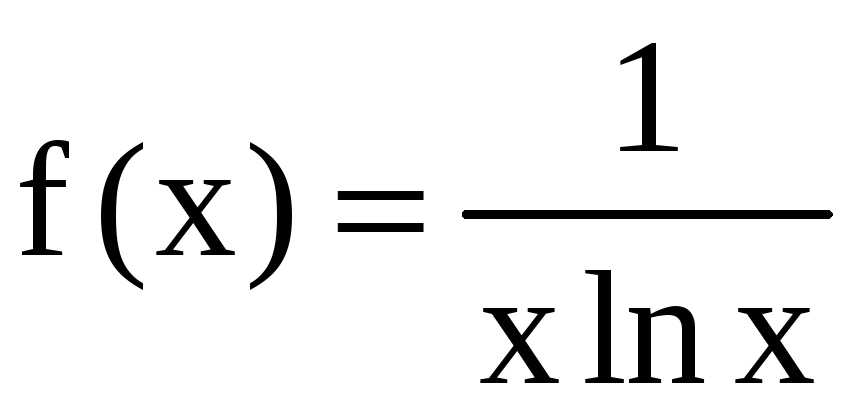 .
Эта функция определена на [2; +),
положительна и монотонно убывает в этом
промежутке. Более того, при n > 2
.
Эта функция определена на [2; +),
положительна и монотонно убывает в этом
промежутке. Более того, при n > 2
 .
Следовательно, согласно теореме 6, ряд
.
Следовательно, согласно теореме 6, ряд
 и несобственный интеграл
и несобственный интеграл
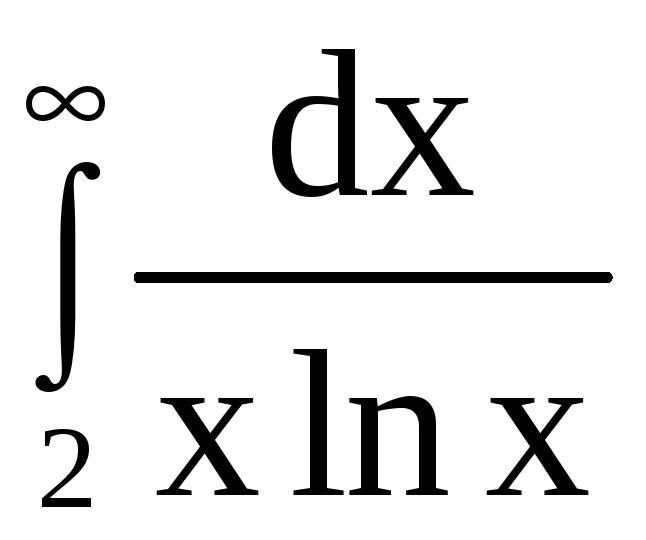 ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
Исследуем интеграл на сходимость:
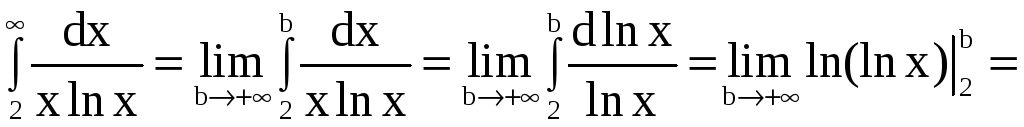
![]() .
.
Видим, что несобственный интеграл расходится, следовательно, расходится и наш ряд.
б)
Рассмотрим функцию
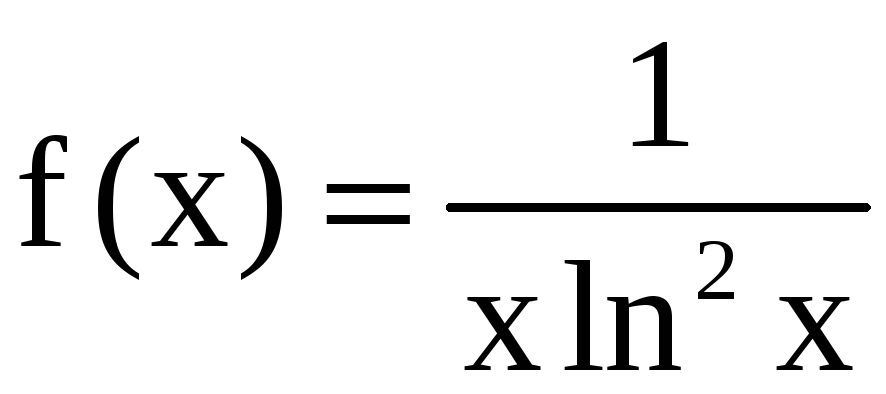 ,
определённую на [2; + ).
Она монотонно убывает и положительна
на [2; +)
и
,
определённую на [2; + ).
Она монотонно убывает и положительна
на [2; +)
и
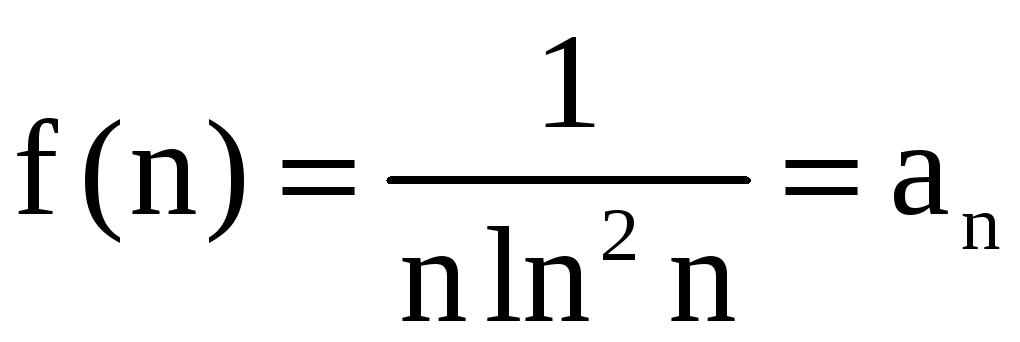 .
Выполнены все требования теоремы 6,
поэтому ряд
.
Выполнены все требования теоремы 6,
поэтому ряд
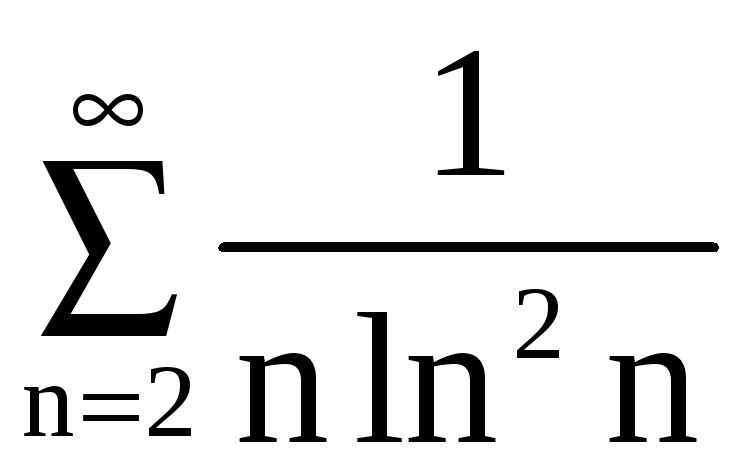 и несобственный интеграл
и несобственный интеграл
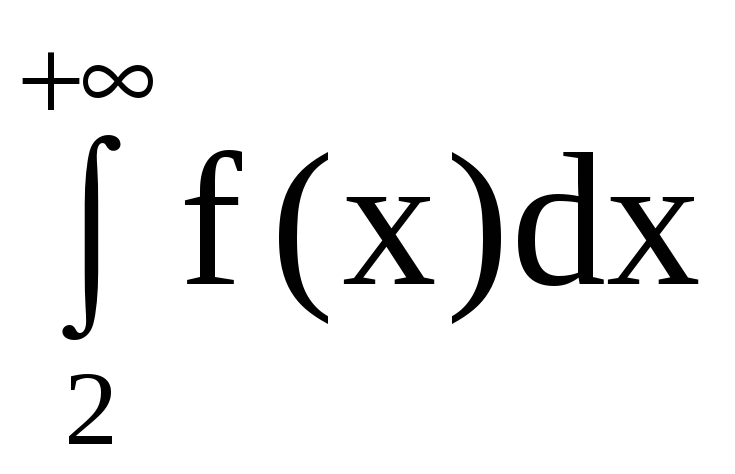 ведут себя одинаково в смысле сходимости.
Имеем
ведут себя одинаково в смысле сходимости.
Имеем
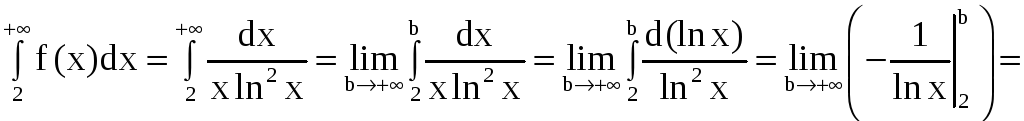
 .
.
Так как несобственный интеграл сходится, то сходится и наш ряд.
