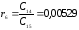Лабораторные работы / исследование устойчивости стационарных и нестационарных линейных / ПР1

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРЕНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»

Практическая работа №1

по дисциплине

Локальные системы управления

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ

СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ

ЛИНЕЙНЫХ И НЕПРЕРЫВНЫХ И

ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Вариант 10

Выполнил ст. гр. УИТ-52в:

Макаров Ю.А.

Проверил преподаватель:

Скоробогатова Т.Н.

2009

Цель работы: изучить методы исследования устойчивости стационарных и нестационарных линейных непрерывных и дискретно непрерывных САР.

Исходная схема имеет вид:

W₁(p)

W₂(p)

W₃(p)

W₅(p)

W₄(p)

–

–

W₆(p)

W₇(p)

Передаточные функции звеньев:

W₁(p) =;

W₂(p) = ;

W₃(p) = 25,72;

W₄(p) = ;

W₅(p) = ;

W₆(p) = 0,093;

W₇(p) = 0,064;

Упростим схему и найдем общую передаточную функцию:

W₁(p)

W₂₃₄(p)

W₅(p)

W₇(p)

W₆(p)

–

–

W₁(p)

W₂₃₄₆(p)

W₅(p)

W₇(p)

–

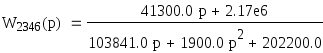
Проведем проверку устойчивости системы несколькими способами.

1 Критерий Ляпунова

Чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Характеристическое уравнение системы:

Определим корни характеристического уравнения в пакете MathCad:

Так как не все корни характеристического уравнения имеют отрицательную вещественную часть, то САУ будет неустойчивой.

2 Критерий Гурвица

Корни характеристического уравнения будут иметь отрицательные действительные части, если составленный из его коэффициентов a_i>0 определитель и все его диагональные миноры положительны.

Запишем характеристическое уравнение системы:

a₀ = 237500; a₁=1,3×10⁷; a₂ = 5,09×10⁸; a₃ = 6,27×10¹⁰; a₄ = 1, 96×10¹².

Теперь можно составить главный определитель Гурвица:

Посчитаем определители:

Из расчетов видно, что все миноры Гурвица положительны, следовательно, система является устойчивой.

3 Критерий Рауса

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса были положительными. Таблица Рауса составляется из коэффициентов характеристического уравнения, которые располагаются в таблице по строкам и столбцам. В первой строке записываются коэффициенты с четными индексами, а во второй – с нечетными. Все остальные клетки таблицы заполняются коэффициентами, которые вычисляются следующим образом:

k – номер столбца в таблице, i – номер строки.

a₀ = 237500; a₁=1,3×10⁷; a₂ = 5,09×10⁸; a₃ = 6,27×10¹⁰; a₄ = 1, 96×10¹²

Составим таблицу Рауса для нашей системы:

	№ i	Номер столбца – k.
		k=1	k=2	k=3
-	1
-	2
	3
	4
	5
	6

Из таблицы видно, что не все коэффициенты положительны. Значит, САУ неустойчива.

4 Критерий Найквиста

Разомкнутая САУ будет устойчивой, если кривая АФЧХ замкнутой системы, имеющей m полюсов в правой полуплоскости, при увеличении от 0 до не будет охватывать точку . На основании передаточной функции системы построим годограф Найквиста.

Используем для этого программу Matlab. В ней необходимо задать следующие команды:

w=tf([7.56*10^9 9.8*10^11 3.06*10^13],[237500 1.3*10^7 5.09*10^8 6.27*10^10 1.96*10^12])

Transfer function:

7.56e009 s^2 + 9.8e011 s + 3.06e013

---------------------------------------------------------------

237500 s^4 + 1.3e007 s^3 + 5.09e008 s^2 + 6.27e010 s + 1.96e012

figure, nyquist(w)

В результате получим годограф Найквиста. По критерию Найквиста система устойчива, поскольку амплитудно-фазовая характеристика не охватывает на комплексной плоскости точку с координатами (-1;j0).

5 Критерий Льенара-Шипара

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах характеристического уравнения все миноры с нечетными индексами были положительными.

a₀ = 237500 > 0

a₁=1,3×10⁷ > 0

a₂ = 5,09×10⁸ > 0

a₃ = 6,27×10¹⁰ > 0

a₄ = 1, 96×10¹² > 0

> 0,

Все условия выполняются. Значит, система устойчива.

6 Критерий Шур-Кона

Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы определители Шур - Кона с нечетными индексами были меньше 0, а с четными индексами были больше 0.

Передаточная функция для замкнутого состояния САУ имеет вид:

Используя средства MathCad, запишем характеристическое уравнение замкнутой системы в форме z-преобразования:

a₀ = 1

a₁ = 54.7

a₂ = 2143

a₃ = 263999

a₄ = 8.25×10⁶

Определитель Шур - Кона имеет вид:

Составим и вычислим четные и нечетные определители Шур-Кона:

к =1

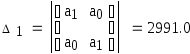
к=2

к=3

к=4

Так как и четные, и нечетные определители больше 0, САУ будет неустойчивой.

7 D-разбиение

Передаточная функция разомкнутой системы имеет вид:

Запишем передаточную функцию с учетом того, что W₂(p)= :

_

W(p)

Передаточная функция замкнутой системы имеет вид:

Характеристическое уравнение такой системы имеет вид:

Произведем замену p=jω, выделим действительную и мнимую части и построим график:

Re(к(jω))=

Im(к(jω))=

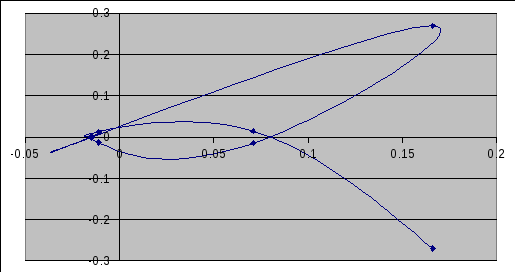
Область D(0), является областью подозрительной на устойчивость.

Проверка:

Пусть к=0,02, тогда характеристическое уравнение примет вид:

По Гурвицу определим устойчивость этой системы:

>0, все коэффициенты уравнения положительные, следовательно, система устойчива в области D(0).