Касательная, нормаль к кривой

Как построить касательную к кривой?

Для построения используем прямые, называемые секущими.

Прямая, пересекающая кривую линию в одной, двух и более точках, называется секущей (АВ).

Чтобы через точку А провести касательную t к кривой m, в окрестности точки А (недалеко) выбирают точку В и проводят секущую АВ. Приближая точку В к точке А в пределе получают касательную t в данной точке.

В  А  АВ  t

Рис. 1-49

Касательную (t в точке А) можно рассматривать как предельное положение секущей, которое занимает последняя при сближении точек пересечения А и В секущей АВ до слияния их в одну точку.

n - нормаль кривой линии в данной точке, n  t. Сколько их можно провести? К пространственной кривой можно провести n  , т.е. к касательной можно построить плоскость, нормальную к ней. Если кривая - плоская, то к касательной можно провести только одну нормаль.

Рассмотренная точка А, у которой только одна касательная и одна нормаль , называется обыкновенной точкой кривой. Если вся кривая состоит из обыкновенных точек, то она называется регулярной (гладкой, плавной).

У регулярной плоской кривой (рис. 1-50) в каждой точке А, В, С, D, Е к касательной можно провести только одну нормаль, поэтому все точки являются обыкновенными(монотонными). Характеристикой плавной кривой может быть и угол наклона касательных относительно оси Х, который в данном случае меняется плавно.

Рис. 1-50

Особые точки кривых линий

Точку кривой называют особой (нерегулярной), если положение или направление касательной в этой точке определено неоднозначно. К особым (нерегулярным) относятся:

Точки узловые (самопересечения)

Точки возврата первого рода

Точки возврата второго рода (клюв)

Точки самосоприкосновения

Точки угловые (точки излома)

Свойства проекций кривых линий

Свойства кривых линий и их проекций позволяют наглядно демонстрировать физические, химические, электрические процессы. В геометрии кривые линии - это линии пересечения поверхностей.

Рис. 1-52

1. Проекцией кривой линии является кривая линия (в общем случае).

2. Касательная к кривой проецируется в касательную к ее проекции.

3. Несобственная точка кривой проецируется в несобственную точку ее проекции.

4. Порядок кривой (только для алгебраических кривых) в проекциях не изменяется.

5. Число точек пересечения кривой сохраняется при проецировании.

Некоторые плоские кривые линии

Эллипс, парабола, гипербола - алгебраические кривые второго порядка определяются уравнением f (х ,у) = 0.

Эллипс

АВ = 2а - большая ось эллипса

CD = 2в - малая ось эллипса

О - центр эллипса

F₁; F₂ - фокусы эллипса

А,В,С,D - вершины эллипса

Точки M и N - любые точки эллипса

MF₁ + MF₂ = NF₁ + NF₂ = АВ - Const

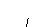
Рис. 1-53

Эллипс - это все множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная, равная 2а.

У эллипса все точки собственные. Кривая симметрична относительно обеих осей. Всегда можно подобрать такую пару диаметров эллипса, что: хорды, параллельные одному диаметру, делятся другим диаметром пополам, такие диаметры называются сопряженными.

Графически можно построить любую точку эллипса, если заданы его оси. Эллипс на рис. 1-54 построен равномерным сжатием окружности в направлении ОС  ОА

АВ - большая ось

СD - малая ось

Разделить окружности на 12 равных частей

Из точек пересечения любого луча с окружностями провести прямые, параллельные осям эллипса:

из точки 1  СD, из точки 2  АВ.

Рис. 1-54