
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
§ 9. Непрерывность функции
9.1. Односторонние пределы
Пусть
![]() .
.
Переменная
![]() может стремиться к
может стремиться к
![]() по-разному:
по-разному:
-
оставаться меньше, чем
 ( слева от
( слева от );
); -
оставаться больше, чем
 (справа от
(справа от
 ).
).
Если рассматривать
![]() ,
то число
,
то число
![]() называется левосторонним
пределом функции в точке
называется левосторонним
пределом функции в точке
![]() .
Обозначается
так:
.
Обозначается
так:
![]() .
.
Если рассматривать
![]() ,
то число
,
то число
![]() называется правосторонним
пределом функции в точке
называется правосторонним
пределом функции в точке
![]() .
.
Обозначается так:
![]() .
.
Эти пределы называются односторонними пределами функции.
-
Понятие непрерывности функции
Определение
1. Пусть
функция
![]() определена в точке
определена в точке
![]() и в некоторой окрестности этой точки.
Функция
и в некоторой окрестности этой точки.
Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если выполняется условие
,
если выполняется условие
![]() .
.
Можно дать еще одно определение непрерывности функции в точке. Для этого введем понятия приращения аргумента и приращения функции.
Пусть функция
![]() определена
определена  в
некотором интервале,
в
некотором интервале,
![]() и
и
![]() – два произвольных значения аргумента
из этого интервала. Разность
– два произвольных значения аргумента
из этого интервала. Разность
![]() называется приращением
аргумента
в точке
называется приращением
аргумента
в точке
![]() .
Разность
.
Разность
![]() называется приращением
функции
в точке
называется приращением
функции
в точке
![]() .
.
Определение
2. Функция
![]() называется
непрерывной
в точке
называется
непрерывной
в точке
![]() ,
если бесконечно малому приращению
аргумента в этой точке соответствует
бесконечно малое приращение функции,
т.е.
,
если бесконечно малому приращению
аргумента в этой точке соответствует
бесконечно малое приращение функции,
т.е.
![]() .
.
Определение
3. Функция
![]() называется непрерывной
на отрезке
называется непрерывной
на отрезке
![]() ,
если она непрерывна в каждой точке
интервала
,
если она непрерывна в каждой точке
интервала
![]() и в точке
и в точке
![]() непрерывна справа (т. е.
непрерывна справа (т. е.
![]() ),
а в точке
),
а в точке
![]() непрерывна слева (т.е.
непрерывна слева (т.е.
![]() ).
).
Важное значение для исследования непрерывности функции имеют следующие теоремы:
-
Основные элементарные функции непрерывны во всех точках, где они определены.
-
Если
 и
и
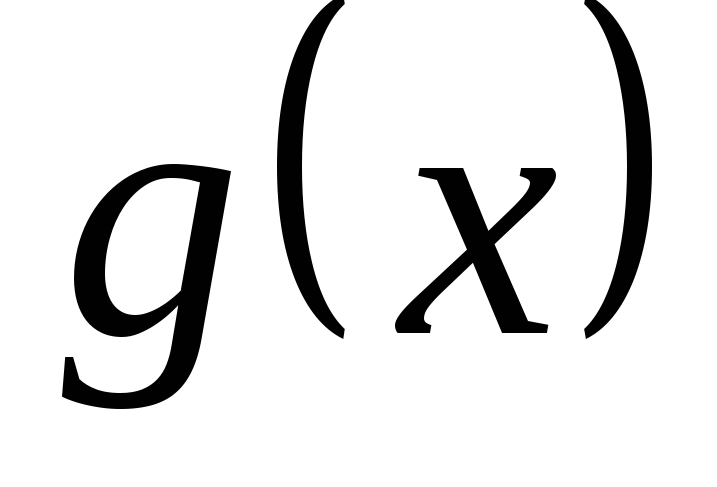 непрерывны в точке
непрерывны в точке
 ,
то в этой же точке непрерывны функции
,
то в этой же точке непрерывны функции
 ;
;
 ;
;
 при
при
 .
. -
Если функция
 непрерывна в точке
непрерывна в точке
 ,
а функция
,
а функция
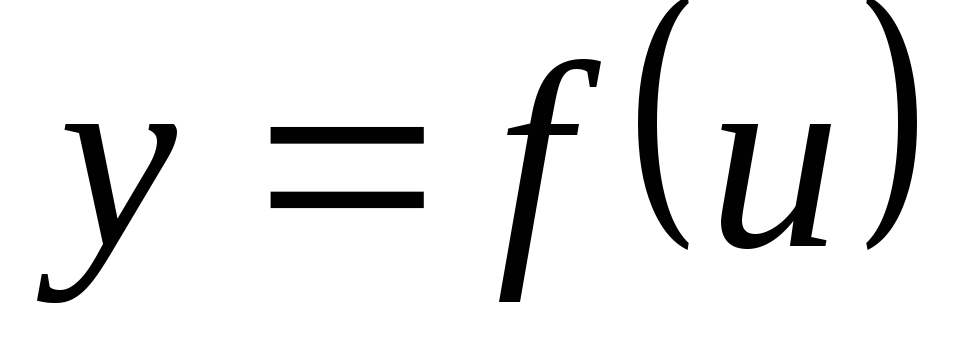 непрерывна в точке
непрерывна в точке
 ,
то сложная функция
,
то сложная функция
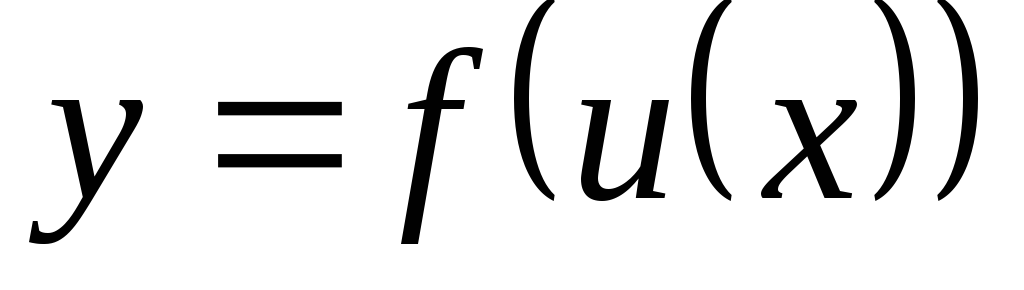 непрерывна в точке
непрерывна в точке
 .
. -
Если функция
 непрерывна и строго монотонна на отрезке
непрерывна и строго монотонна на отрезке
 оси
оси
 ,
то и обратная ей функция
,
то и обратная ей функция
 непрерывна и строго монотонна на
соответствующем отрезке
непрерывна и строго монотонна на
соответствующем отрезке
 оси
оси
 .
.
-
Классификация точек разрыва функции
Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Все точки разрыва функции делятся на точки разрыва первого и второго рода.
Определение.
Точка разрыва
![]() называется точкой
разрыва
первого рода,
если в этой точке существуют конечные
односторонние пределы:
называется точкой
разрыва
первого рода,
если в этой точке существуют конечные
односторонние пределы:
![]() и
и
![]() .
.
При этом: а) если
![]() то точка разрыва называется точкой
устранимого разрыва;
б) если
то точка разрыва называется точкой
устранимого разрыва;
б) если
![]() ,
то точка разрыва называется точкой
конечного разрыва.
,
то точка разрыва называется точкой
конечного разрыва.
Величину
![]() называют скачком
функции
в точке разрыва первого рода.
называют скачком
функции
в точке разрыва первого рода.
Определение.
Точка
![]() называется точкой
разрыва
второго рода,
если хотя бы один из односторонних
пределов не существует или равен
бесконечности.
называется точкой
разрыва
второго рода,
если хотя бы один из односторонних
пределов не существует или равен
бесконечности.
Пример 1.
Доказать, что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
¦
1) По первому определению:
![]() .
.
2) По второму определению:
![]()
![]() .
.
Пример 2.
Исследовать
функцию
![]() на непрерывность.
на непрерывность.
¦
![]() – точка разрыва.
– точка разрыва.
![]()
 не существует, в
других точках
не существует, в
других точках
![]() .
.
![]()
![]()
![]() – устранимый
разрыв.
– устранимый
разрыв.
Функцию в точке
![]() можно доопределить
можно доопределить

Пример 3. Найти точки разрыва функции и определить их вид.


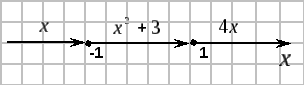
¦
![]()

в точке
![]() разрыв первого рода.
разрыв первого рода.
![]()
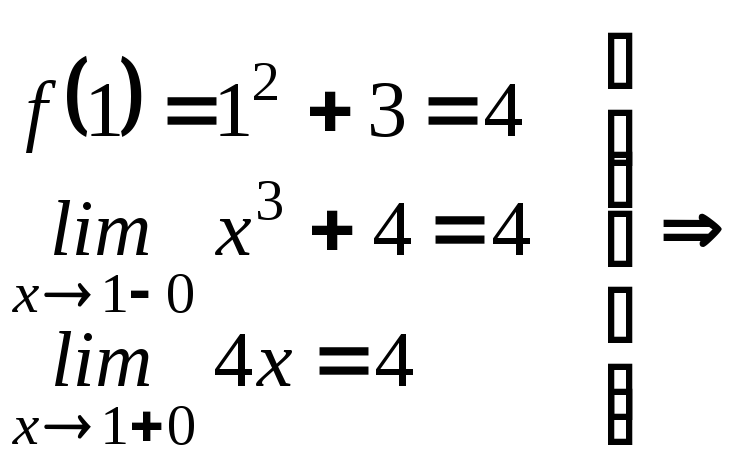
в точке
![]() функция непрерывна.
функция непрерывна.
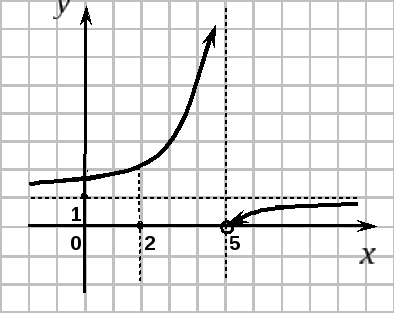
Пример 4.
Исследовать функцию
![]() на непрерывность
на непрерывность
в точках
![]() и
и
![]() .
.
¦
1)
![]()
![]()
![]() – функция непрерывна.
– функция непрерывна.
 2)
2)
![]()
![]() не существует – следовательно,
не существует – следовательно,
![]() - точка разрава
- точка разрава
![]()
![]()
Имеем разрыв II рода.
![]() .
.
