§ 6. Предел функции

6.1. Предел функции в точке

Пусть функция определена в некоторой окрестности точки , причем в самой точке функция может быть и не определена.

Определение. Число называется пределом функции в точке ( или при ), если для любого положительного числа найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство . Записывают .

Коротко можно записать так:

Геометрический смысл:

, если для любой – окрестности точки найдется такая – окрестность точки , что для всех из этой –окрестности соответствующие значения функции лежат в – окрестности точки . Т.е. точки графика лежат внутри полосы шириной , ограниченной линиями и . Очевидно, что величина зависит от . Поэтому пишут .

Пример 1. Доказать, что .

¦ Возьмем произвольное число . Найдем по этому такое значение , при котором из неравенства следовало бы неравенство . Преобразуя последнее неравенство, получаем или . Отсюда видно, что если взять , то для всех , удовлетворяющих , выполняется неравенство . Это и означает, что . ¢

Пример 2. Доказать, что .

¦ Для любого можно взять любое . Тогда при , имеем . ¢

6.2. Предел функции при

Пусть функция определена на .

Определение. Число называется пределом функции при , если для любого положительного числа существует такое число , что при всех , удовлетворяющих неравенству , выполняется неравенство . Коротко можно записать так:

Геометрический смысл этого определения таков: , что при или при соответствующие значения функции попадают в – окрестность точки , т.е. точки графика лежат в полосе шириной , ограниченной прямыми и .

Сформулируем теперь понятие предела функции при .

Определение. Число называется пределом функции при (соответственно при ), если для любого положительного числа существует такое число , что при всех , удовлетворяющих неравенству (соответственно ), выполняется неравенство .

Если , то пишут .

Если , то пишут .

6.3. Теоремы о пределах функций

При вычислении пределов необходимо знать следующие теоремы.

Формулировки теорем аналогичны для случаев, когда и . Будем считать, что пределы и существуют.

1. Функция может иметь только один предел.

2. .

3. .

4. . (выполняется для любого числа слагаемых)

5. .

6. , если .

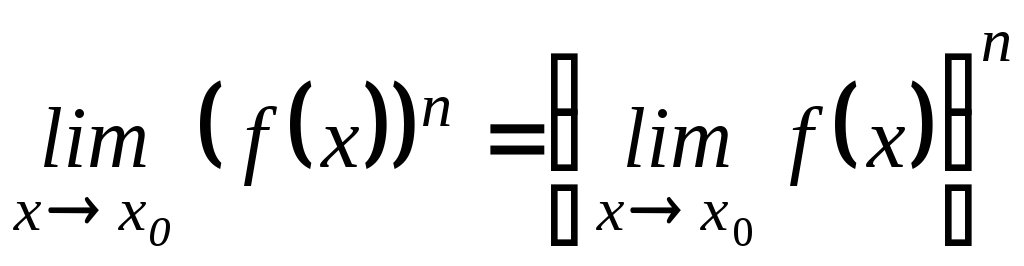7. предел степени равен степени предела.

В частности,

8. Для всех основных элементарных функций в любой точке их области определения имеет место равенство .

9. Теорема о пределе промежуточной функции.

Пусть функции , , определены в некоторой окрестности точки , причем в самой точке функции могут быть и не определены.

Если и ,то .

Примем эти теоремы без доказательства.

Примеры вычисления пределов с помощью перечисленных теорем.

1. .		2. .
3. .	4. .