
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
15.4. Асимптоты графика функций
При исследовании
поведения функции при
![]() или вблизи точек разрыва второго рода
часто бывает, что график сколь угодно
близко приближается к той или иной
прямой. Такие прямые называются
асимптотами.
или вблизи точек разрыва второго рода
часто бывает, что график сколь угодно
близко приближается к той или иной
прямой. Такие прямые называются
асимптотами.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
1. Прямая
![]() является
вертикальной
асимптотой,
если хотя бы один из пределов
является
вертикальной
асимптотой,
если хотя бы один из пределов
![]() или
или
![]() равен
равен
![]() или
или
![]() .
.
2. Если
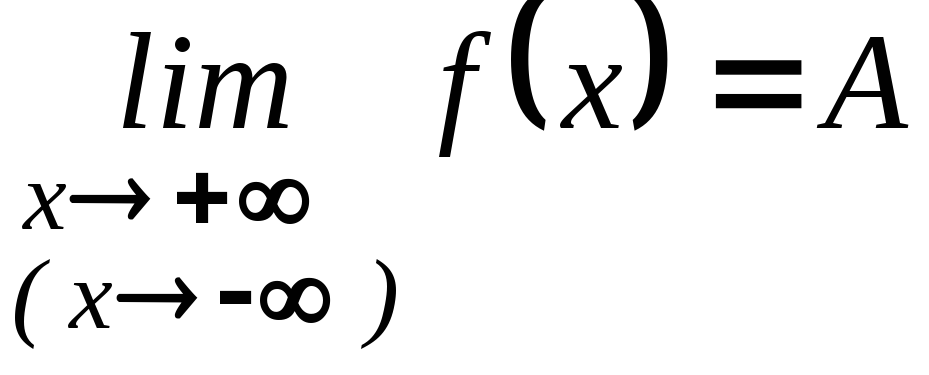 ,
то прямая
,
то прямая
![]() является горизонтальной
асимтотой.
является горизонтальной
асимтотой.
3. Если существует
такие числа
![]() и
и
![]() ,
что
,
что
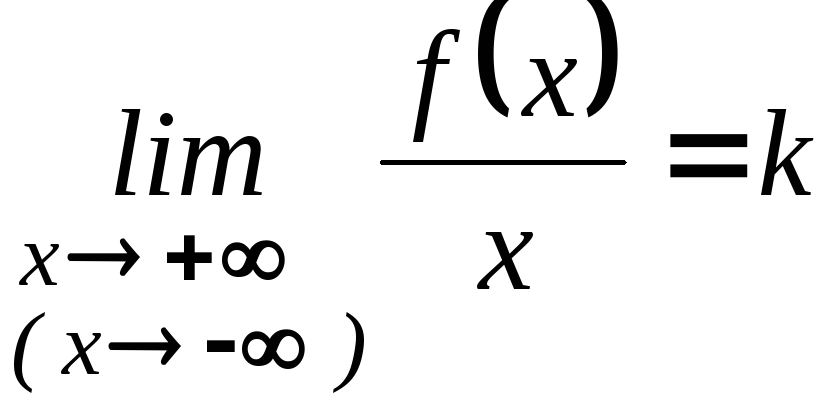 и
и
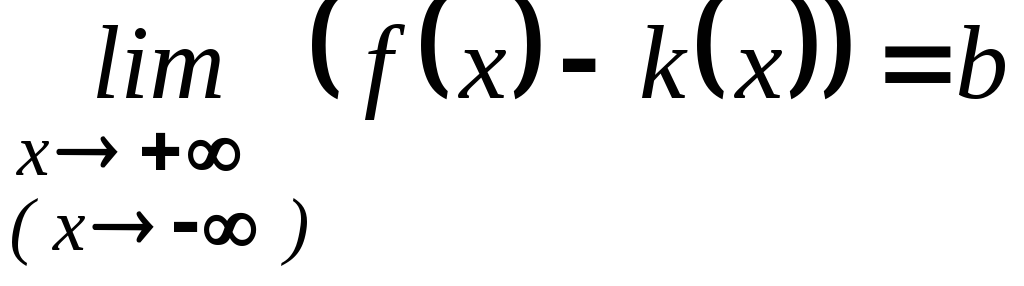 ,
то прямая
,
то прямая
![]() является наклонной
асимптотой.
является наклонной
асимптотой.
Если
![]() ,
,
![]() , то это горизонтальная асимптота.
, то это горизонтальная асимптота.
Если
![]() или
или
![]() ,
то наклонных асимптот у графика нет.
,
то наклонных асимптот у графика нет.
15.5. Общая схема исследования функции
-
Находим область определения функции (если есть точки разрыва, то находим односторонние пределы в этих точках).
-
Проверяем, является ли функция четной, нечетной или общего вида.
-
Находим точки пересечения графика функции с осями координат.
-
Находим асимптоты.
-
Определяем промежутки монотонности и экстремумы.
-
Определяем выпуклость графика функции и точки перегиба.
-
Строим график.
Пример. Исследовать
функцию
![]() .
.
-
Находим область определения функции.
![]()
![]()
![]() – точка разрыва
– точка разрыва
![]()
![]()
2. Определяем четность или нечетность функции.
Функция - общего вида, так как ее область определения несимметрична относительно начала координат.
3.Находим точки пересечения с осями координат.
с осью
![]() :
:
![]()
![]() точек пересечения нет;
точек пересечения нет;
с осью
![]() :
:
![]()
![]()
![]() .
.
4. Находим асимптоты графика функции.
1)![]() - это вертикальная асимптота.
- это вертикальная асимптота.
2) При
![]()
![]() горизонтальных асимптот нет
горизонтальных асимптот нет
3)
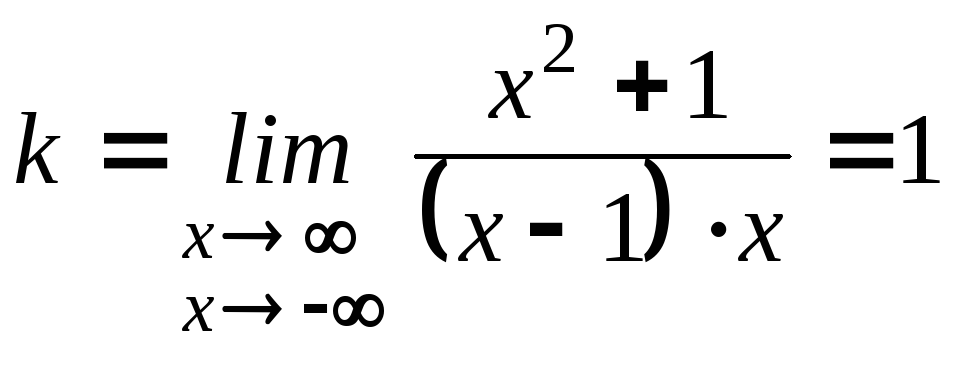 ,
,
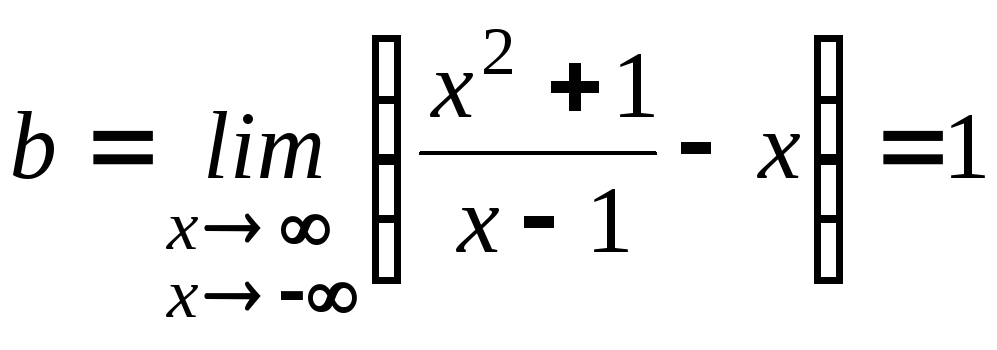
![]()
![]() – это наклонная
асимптота.
– это наклонная
асимптота.
5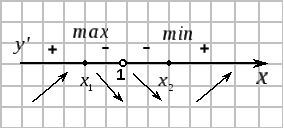 .
Находим промежутки монотонности и
экстремумы функции.
.
Находим промежутки монотонности и
экстремумы функции.
![]() .
.
![]() при
при
![]() ,
,
![]() .
.
Критические точки и точку разрыва функции отмечаем на числовой прямой.
![]() –
это точка максимума функции,
–
это точка максимума функции,
![]() –
это точка минимума функции.
–
это точка минимума функции.
![]() ,
,
![]() .
.
6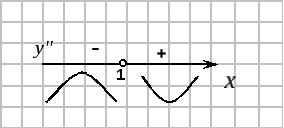 .
Находим промежутки выпуклости и точки
перегиба графика функции.
.
Находим промежутки выпуклости и точки
перегиба графика функции.
![]() ,
,
![]()
![]() на прямой отмечаем только точку разрыва
функции
на прямой отмечаем только точку разрыва
функции
7.Строим график функции .
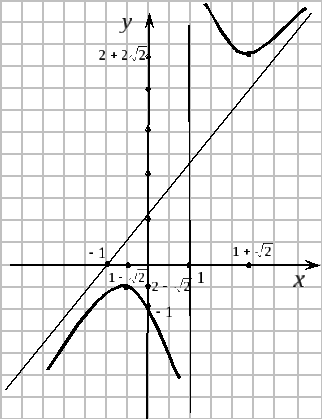
15.6. Наибольшее и наименьшее значение функции на отрезке
Пусть функция
![]() определена и дифференцируема на отрезке
определена и дифференцируема на отрезке
![]() .
Она может достигать своего наибольшего
и наименьшего значения на отрезке
.
Она может достигать своего наибольшего
и наименьшего значения на отрезке
![]() в точках экстремума, принадлежащих
этому отрезку или на концах отрезка :
в точках
в точках экстремума, принадлежащих
этому отрезку или на концах отрезка :
в точках
![]() и
и
![]() .
.
План исследования.
-
Находим точки, принадлежащие отрезку
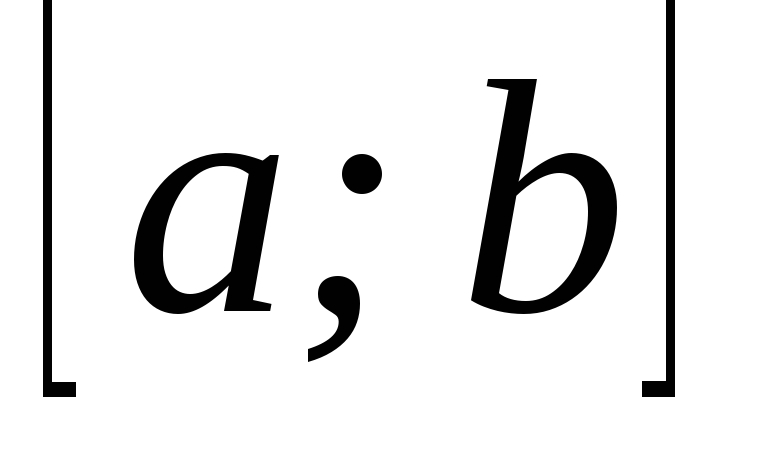 ,
в которых
,
в которых
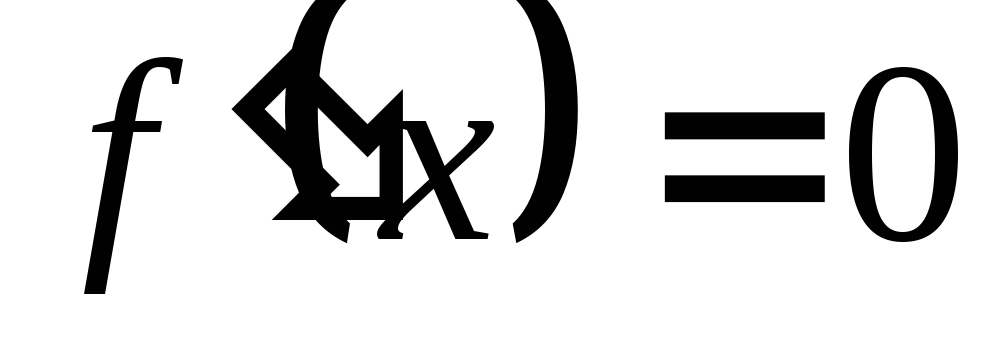 .
.
-
Находим значения функции в выбранных точках и на концах отрезка.
-
Выбираем самое наибольшее и самое наименьшее значения функции.
Они обозначаются
так:
![]() и
и
![]() .
.
Пример. Найти наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке
![]() .
.
1. Находим точки,
принадлежащие отрезку
![]() ,
в которых
,
в которых
![]() .
.
![]()
![]()
![]()
![]()
![]()
2. Находим значения функции в выбранных точках и на концах отрезка.
![]() ;
;
![]() ;
;
![]() .
.
3. Выбираем самое наибольшее и самое наименьшее значения функции.
Ответ:
![]() и
и
![]() .
.
