
- •Содержание
- •Глава I. Функция и ее предел
- •§ 1. Множества
- •§ 2. Понятие функции
- •§ 3. Основные характеристики функции
- •§ 4. Классификация функций
- •4.1. Обратная функция
- •4.2. Сложная функция
- •4.3. Основные элементарные функции и их графики
- •§ 5. Числовые последовательности
- •§ 6. Предел функции
- •6.1. Предел функции в точке
- •6.2. Предел функции при
- •6.3. Теоремы о пределах функций
- •6.4. Два замечательных предела
- •§ 7. Бесконечно большие и бесконечно малые функции
- •7.1. Бесконечно большие функции и их свойства
- •7.2. Бесконечно малые функции и их свойства
- •7.3. Связь между функцией, ее пределом и б. М. Ф.
- •7.4. Сравнение бесконечно малых функций
- •§ 8. Вычисление пределов функции
- •§ 9. Непрерывность функции
- •9.1. Односторонние пределы
- •Понятие непрерывности функции
- •Классификация точек разрыва функции
- •9.4. Свойства функций, непрерывных на отрезке
- •Глава II. Дифференциальное исчисление
- •§ 10. Понятие производной, ее геометрический и физический смысл
- •10.1. Определение производной
- •10.2. Геометрический смысл производной
- •10.3. Физический смысл производной
- •§ 11. Правила дифференцирования функций и производные элементарных функций
- •Правила дифференцирования
- •11.2. Производные элементарных функций
- •11.3. Логарифмическое дифференцирование
- •11.4. Производные высших порядков
- •Производная неявной функции
- •11.6. Производная функции, заданной параметрически
- •§ 12. Дифференциал функции
- •§ 13. Основные теоремы дифференциального исчисления
- •Геометрический смысл теоремы Ролля.
- •§ 14. Правило Лопиталя
- •14.1. Теорема Лопиталя
- •14.2. Другие виды неопределенностей и их раскрытие
- •§ 15. Исследование функций при помощи производных
- •15.1. Признак монотонности функции Необходимое условие экстремума функции
- •15.2. Достаточные условия экстремума
- •15.3. Направление выпуклости и точки перегиба графика функции
- •15.4. Асимптоты графика функций
- •15.5. Общая схема исследования функции
- •15.6. Наибольшее и наименьшее значение функции на отрезке
- •Литература
§ 15. Исследование функций при помощи производных
15.1. Признак монотонности функции Необходимое условие экстремума функции
Теорема.
Если функция
![]() дифференцируема на интервале
дифференцируема на интервале
![]() и
и
![]()
![]() на
на
![]() ,
то функция
,
то функция
![]() не убывает ( не возрастает) на
не убывает ( не возрастает) на
![]() .
.
Если
![]()
![]() на
на
![]() ,
то
,
то
![]() возрастает (убывает) на
возрастает (убывает) на
![]() .
.
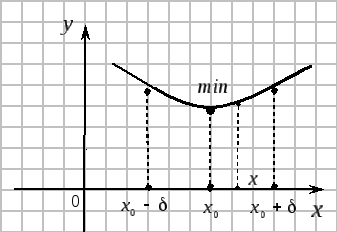 Определение.
Точка
Определение.
Точка
![]() называется точкой локального
максимума
(минимума)
фуннкции
называется точкой локального
максимума
(минимума)
фуннкции
![]() ,
если для всех
,
если для всех
![]() из
некоторой
из
некоторой
![]() -
окрестности точки
-
окрестности точки
![]() выполняется неравенство
выполняется неравенство
![]()
![]() при
при
![]() .
.

Максимум (![]() )
и минимум (
)
и минимум (![]() )
называются экстремумами
функции.
)
называются экстремумами
функции.
Теорема (необходимое условие экстремума).
Если функция
![]() имеет в точке
имеет в точке
![]() экстремум
и дифференцируема в этой точке, то
экстремум
и дифференцируема в этой точке, то
![]() .
.
Такие точки называются точками возможного экстремума или критическими или стационарными.
Если
![]() – критическая
точка, то она может и не быть точкой
экстремума.
– критическая
точка, то она может и не быть точкой
экстремума.
Например:
![]() ,
,
![]() при
при
![]() ,
но в точке
,
но в точке
![]() нет экстремума.
нет экстремума.
Поэтому условие
![]() является необходимым, но не достаточным,
а точка
является необходимым, но не достаточным,
а точка
![]() -
это точка возможного экстремума.
-
это точка возможного экстремума.
15.2. Достаточные условия экстремума
Теорема (первое достаточное условие).
Пусть
![]() критическая точка.
Если
критическая точка.
Если
![]() при переходе через точку
при переходе через точку
![]() меняет знак с «+» на «-», то
меняет знак с «+» на «-», то
![]() является точкой локального
максимума.
является точкой локального
максимума.
Если
![]() при переходе через точку
при переходе через точку
![]() меняет знак с «-» на «+», то
меняет знак с «-» на «+», то
![]() является точкой локального
минимума.
Если
является точкой локального
минимума.
Если
![]() при переходе через точку
при переходе через точку
![]() не меняет знак, то экстремума в этой
точке нет.
не меняет знак, то экстремума в этой
точке нет.
Значения
функции
![]() в точках максимума и минимума называются
соответственно максимум
и минимум
функции и обозначаются:
в точках максимума и минимума называются
соответственно максимум
и минимум
функции и обозначаются:
![]() ,
,
![]() .
Максимум и минимум называются экстремумами
функции.
.
Максимум и минимум называются экстремумами
функции.
Схема исследования функции на экстремум.
Пусть
![]() ,
,
![]() ,
,
![]() – это
– это
к ритические
точки. Отметим
их
ритические
точки. Отметим
их
на числовой прямой.
Из рисунка видно, что
![]() – это точка
максимума, тогда
– это точка
максимума, тогда
![]() ;
;
![]() –
это точка минимума
, тогда
–
это точка минимума
, тогда
![]() ;
;
![]() не является точкой
экстремума.
не является точкой
экстремума.
В случае, когда исследование знака первой производной слева и справа от критической точки затруднено, можно использовать второе достаточное условие.
Теорема (второе достаточное условие).
Пусть функция
![]() имеет в данной критической точке
имеет в данной критической точке
![]() конечную вторую производную. Тогда
функция
конечную вторую производную. Тогда
функция
![]() имеет в точке
имеет в точке
![]() локальный максимум, если
локальный максимум, если
![]() ,
и локальный минимум если
,
и локальный минимум если
![]() .
.
15.3. Направление выпуклости и точки перегиба графика функции
Пусть функция
![]() дифференцируема на интервале
дифференцируема на интервале
![]() .
Тогда в любой точке этого интервала
существует касательная к графику
функции
.
Тогда в любой точке этого интервала
существует касательная к графику
функции
![]() ,
проходящая через точку
,
проходящая через точку
![]() этого графика.
этого графика.
Будем говорить:
-
 график
функции
график
функции
 на
на
 имеет выпуклость,
направленную
вниз , если
он расположен не ниже любой касательной
к графику функции на этом интервале;
имеет выпуклость,
направленную
вниз , если
он расположен не ниже любой касательной
к графику функции на этом интервале;
2 )
график функции
)
график функции
![]() на
на
![]() имеет выпуклость
, направленную
вверх ,
если он расположен не выше любой
касательной к графику функции на этом
интервале.
имеет выпуклость
, направленную
вверх ,
если он расположен не выше любой
касательной к графику функции на этом
интервале.

Если в точке
![]() график функции
график функции
![]() меняет направление выпуклости, то
меняет направление выпуклости, то
![]() называют точкой
перегиба графика.
называют точкой
перегиба графика.
Необходимое условие точки перегиба.
Если в точке
![]() график функции имеет перегиб и непрерывную
вторую производную, то
график функции имеет перегиб и непрерывную
вторую производную, то
![]() .
.
 Следует
заметить, что не всякая точка
Следует
заметить, что не всякая точка
![]() ,
в которой
,
в которой
![]() ,
является точкой перегиба.
,
является точкой перегиба.
Такие точки будем называть критическими, или точками возможного перегиба.
Например:
![]() ,
,
![]() ,
,
![]() при
при
![]() ,
но
,
но
![]() не является точкой перегиба.
не является точкой перегиба.
Необходимо дополнительное исследование каждой критической точки.
Достаточное условие точки перегиба.
Пусть функция
![]() имеет вторую производную в некоторой
окрестности точки
имеет вторую производную в некоторой
окрестности точки
![]() и
и
![]() .
Тогда, если вторая производная
.
Тогда, если вторая производная
![]() при переходе через критическую точку
при переходе через критическую точку
![]() меняет знак, то
меняет знак, то
![]() является точкой перегиба.
является точкой перегиба.
Замечание.
Если на некотором интервале
![]() ,
то график функции имеет выпуклость
вниз, если
,
то график функции имеет выпуклость
вниз, если
![]() ,
то график функции имеет выпуклость
вверх.
,
то график функции имеет выпуклость
вверх.
Схема исследования графика функции на выпуклость.
Пусть
![]() в точках
в точках
![]() и
и
![]() .
.
И з
рисунка видно, что
з
рисунка видно, что
![]() есть точка перегиба;
есть точка перегиба;
![]() не является точкой
перегиба.
не является точкой
перегиба.
