
Лабораторные работы / ЛР / №1
.1.docМинистерство высшего и профессионального образования РФ.
Саратовский Государственный Технический Университет.
Балаковский Институт Техники Технологии и Управления.
Факультет: вечерне-заочного обучения.
Кафедра: Управление и Информатика в Технических Системах.
Специальность: Управление и Информатика в Технических Системах.
Дисциплина: Локальные Системы Управления.
Практическая работа №1.
Выполнил: студент группы УИТ 51-в
Муллаев А.Н.
Принял: преподаватель
Стельмах И.В.
Балаково 2003 г.
Задание:
Исследовать устойчивость одноконтурной системы автоматического регулирования с помощью логарифмических амплитудных и фазовых частотных характеристик, если передаточная функция разомкнутой системы:
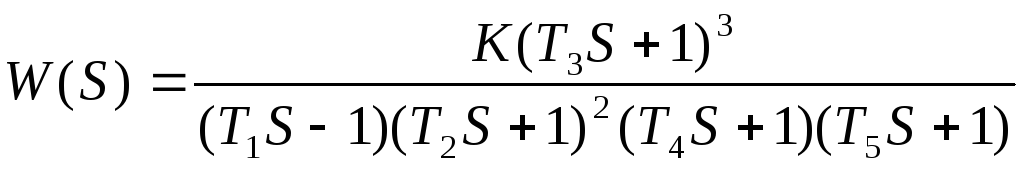 ,
где
,
где
Т1= 25 с ; Т2= 5 с ; Т3= 0,5 с ; Т4= 0,0025 с ; К1= 100 ; К2= 40000.
Определить запасы устойчивости системы по фазе и по модулю.
Решение:
Исследуем устойчивость системы управления по критерию Найквиста.
Этот критерий даёт возможность судить об устойчивости замкнутой СУ, исследуя разомкнутую систему. Для этого определим устойчивость разомкнутой системы. Применим алгебраический критерий Рауса-Гурвица.
Найдём характеристическое уравнение передаточной функции разомкнутой системы.
![]()
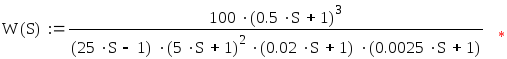
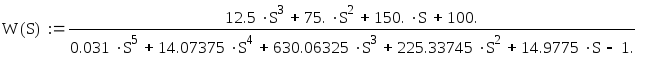
![]()
(t)-выходная величина СУ, (t)-входная величина СУ.
Выделим характеристическое уравнение.
![]()
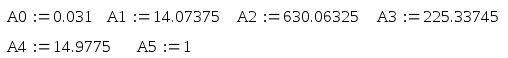
Для устойчивости разомкнутой системы, имеющей характеристическое уравнение пятого порядка, необходимо и достаточно, чтобы все коэффициенты этого уравнения, а также определители 2, 3, ∆4 были положительными:
А0>0; A1>0; A2>0; A3>0; A4>0; A5>0.
![]()

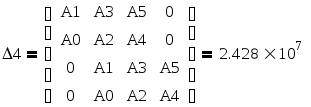
Данная разомкнутая система устойчива.
Из критерия Найквиста следует, что в случае устойчивой разомкнутой системы для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала точку (-1; j0) и не проходила через неё.
Построим АФХ разомкнутой системы.
АФХ это годограф вектора изображающего на комплексной плоскости частотную передаточную функцию W(jw) при изменении частоты w от 0 до . Для этого заменим, оператор S на (jw) и выделим мнимую jV(w) и действительную U(w) часть передаточной функции W(jw).
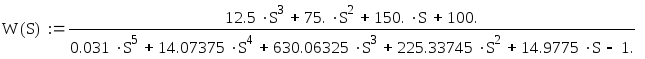
![]()

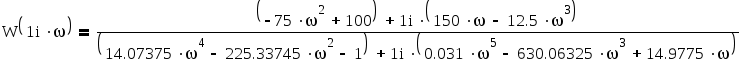
![]()
Приведём уравнение к виду:
![]()
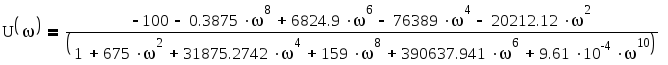
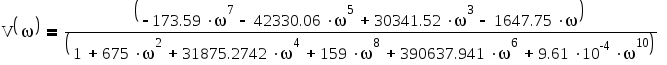
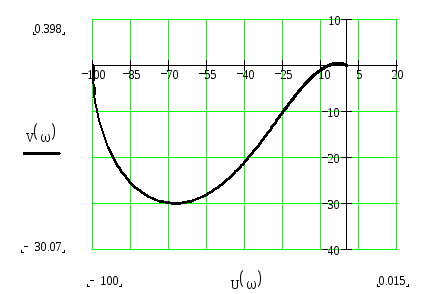
График 1.1
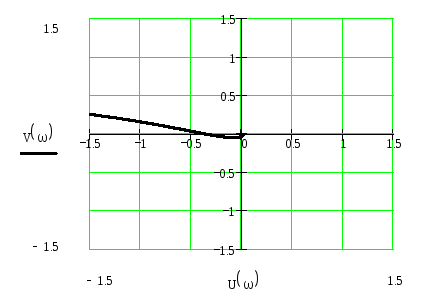
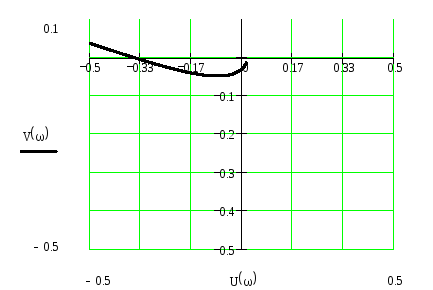
График 1.2
Определим запасы устойчивости системы регулирования по амплитуде и по фазе.
При исследовании устойчивости системы по амплитудно-фазовым характеристикам, обычно пользуются такими величинами оценки запаса устойчивости системы, как запас устойчивости по амплитуде L и запас устойчивости по фазе .
Запас устойчивости по амплитуде показывает, на какую величину должен измениться модуль амплитудно-фазовой характеристики системы на частоте w=wср, для того чтобы система оказалась на границе устойчивости.
Частота среза системы представляет собой значение частоты w, при котором выполняется равенство
A(w)=[W(jw)]=1.
Геометрически частота среза представляет собой частоту, при которой амплитудно-фазовая характеристика W(jw) пересекает окружность единичного радиуса с центром в начале координат. Запас устойчивости будет определяться расстоянием от точки пересечения амплитудно-фазовой характеристики с отрицательной вещественной полуосью до точки [-1, j0].
Запасом устойчивости по фазе или избытком фазы устойчивой замкнутой системы называется увеличение запаздывания по фазе на частоте среза (т.е при значении частоты w, при котором амплитудно-фазовая характеристика системы входит внутрь круга единичного радиуса и в дальнейшем не выходит из него), при котором система доходит до границы области устойчивости.
Из графика N1.2 найдём запас устойчивости по амплитуде L и запас устойчивости
по фазе .
L=(0,67/1)100%=67%
=(180-(ср)) =180°-190°= -10°
Из графиков 1.1 и 1.2 видно, что кривая обходит точку с координатой (-1, j0). Из этого следует, что данная одноконтурная система автоматического регулирования устойчива.
Построим график АЧХ.
Модуль АФХ или отношение амплитуд выходного и входного колебаний, функции их частоты ω называется амплитудночастотной характеристикой.
![]()
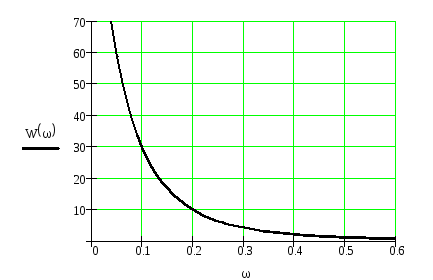
График №2.
Построим ЛАЧХ
ЛАЧХ определяет изменение логарифма модуля частотной функции при изменении частоты ω.
![]()
![]()
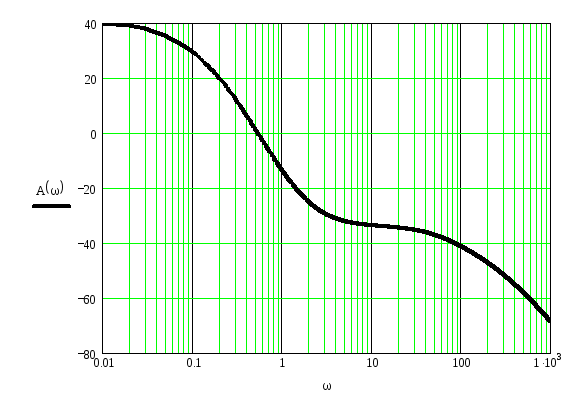
График № 4
ЛАЧХ может быть представлена ломаной линией, это приближённая характеристика называется асимптотической, так как она составлена из асимптот, к которым стремится ЛАЧХ при частоте, стремящейся к 0 и частоте, стремящейся к ∞. Найдем эти асимптоты.
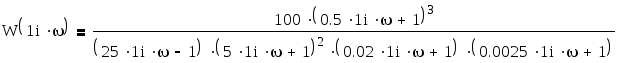
Для этого перепишем её в виде:
![]()
![]()
Определим сопрягающие частоты.
![]()
![]()
![]()
![]()
![]()
При частоте ω=0 L(ω)= 20Lg(100) = 40 дБ, поэтому от частоты ω=0 1/С до ω1=0,041/С асимптота представляет собой прямую параллельную оси абсцисс.
От частоты ω1 = 0,04 1/С
до ω2
= 0,2 1/С
асимптота
пройдёт под наклоном -20 дБ на декаду,
соответствующему звену
![]() .
.
От частоты ω2
= 0,2 1/С
до частоты ω3
= 2 1/С
к наклону
асимптоты -20 дБ на декаду прибавится
наклон -40 дБ на декаду, соответствующий
звену
![]() .
Общий наклон асимптоты на этом участке
, будет -60 дБ на декаду. При частоте ω = 1
L(ω)
=-13,36 дБ (точка А, график 5)
.
Общий наклон асимптоты на этом участке
, будет -60 дБ на декаду. При частоте ω = 1
L(ω)
=-13,36 дБ (точка А, график 5)
От частоты ω3
= 2 1/С
до частоты ω4
= 50 1/С
к наклону -60 дБ
на декаду прибавится наклон +60 дБ на
декаду, соответствующий звену
![]() .
Общий наклон асимптоты на этом участке
составит 0°.
.
Общий наклон асимптоты на этом участке
составит 0°.
От частоты ω4
= 50 1/С
до частоты ω5
= 400 1/С
наклон асимптоты -20 дБ на декаду,
соответствующий звену
![]() .
.
От частоты ω5 = 400 1/С общий наклон асимптоты составит -40 дБ на декаду.
Построим ЛФЧХ.
Логарифмическая фазовая частотная характеристика определяет изменение фазы в градусах при изменении частоты от -∞ до +∞.
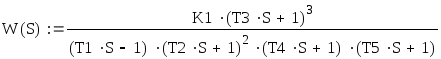
Перепишем передаточную функцию в виде:
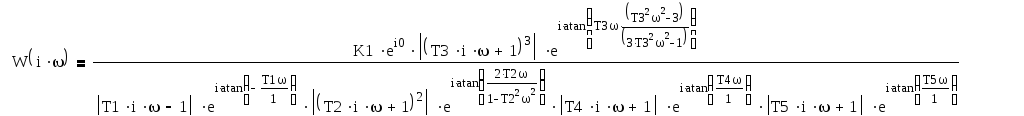
![]()
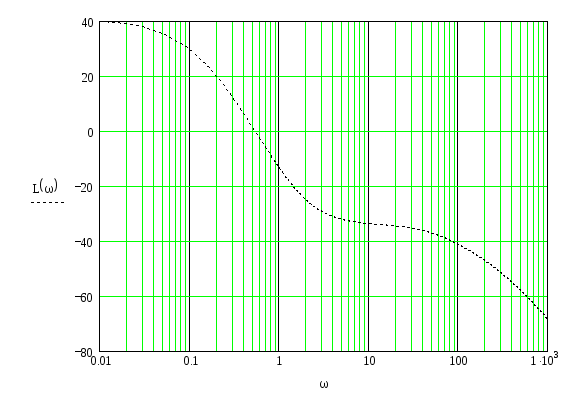
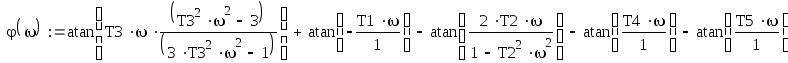
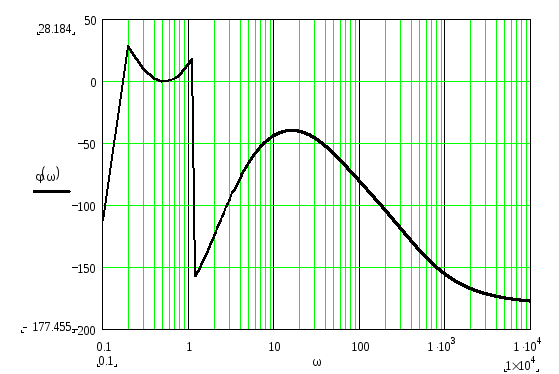
График № 5а, 5б.
