-
Понятие равномерно распределённой непрерывной случайной величины (нсв). Вычисление вероятностей для равномерно распределённой нсв. Характеристики равномерно распределенной нсв.
Ответ:
Равномерно распределённой непрерывной случайной величины – СВ, имеющая постоянную плотность распределения на интервале [a,b], а в не этого интервала плотность равна нулю.
Вычисление вероятностей для равномерно распределённой НСВ:
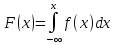
Мат. Ожидание:
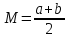
Дисперсия:
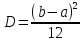
СКО:
-
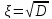
Расчёт вероятности для непрерывной случайной величины (нсв). Вычисление математического ожидания, дисперсии, среднеквадратического отклонения нсв.
Ответ:
Расчёт вероятности для непрерывной случайной величины:
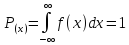
Мат. Ожидание:
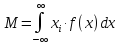
Дисперсия:
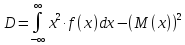
СКО:
-
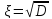
Генеральная совокупность и выборка. Дискретные и интервальные вариационные ряды. Числовые характеристики выборки.
Ответ:
Генеральная совокупность – это множество всех возможных значений, наблюдений, объектов относительно некоторого условия.
Выборка – совокупность случайно отобранных объектов для непосредственного изучения.
Дискретный вариационный ряд - ряд распределения, позволяющий представить совокупность данных в виде конечного множества округленных значений.
Интервальный вариационных ряд – ряд распределения, значения признака которого представлены в виде интервалов значений.
Числовые характеристики выборки:
-
Размах варьирования:
-
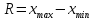
Мода – значение, для которого частота встречаемости в выборке максимальна.
-
Медиана упорядоченного ряда с нечетным числом членов – число, записанное посредине ряда, а медиана упорядоченного ряда с четным числом членов – среднее арифметическое 2х чисел, записанных посредине.
-
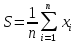
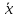Среднее значение выборки:
-среднее
значение выборки
-
Дисперсия:
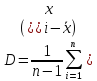
6) СКО:
-
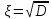
Графическое представление статистических рядов. Полигон и гистограмма.
Ответ:
Для наглядности принято использовать следующие формы графического представления статистических распределений: полигоны и гистограммы.
Полигон частот – это ломаная линия, отрезки которой соединяют значения частот.
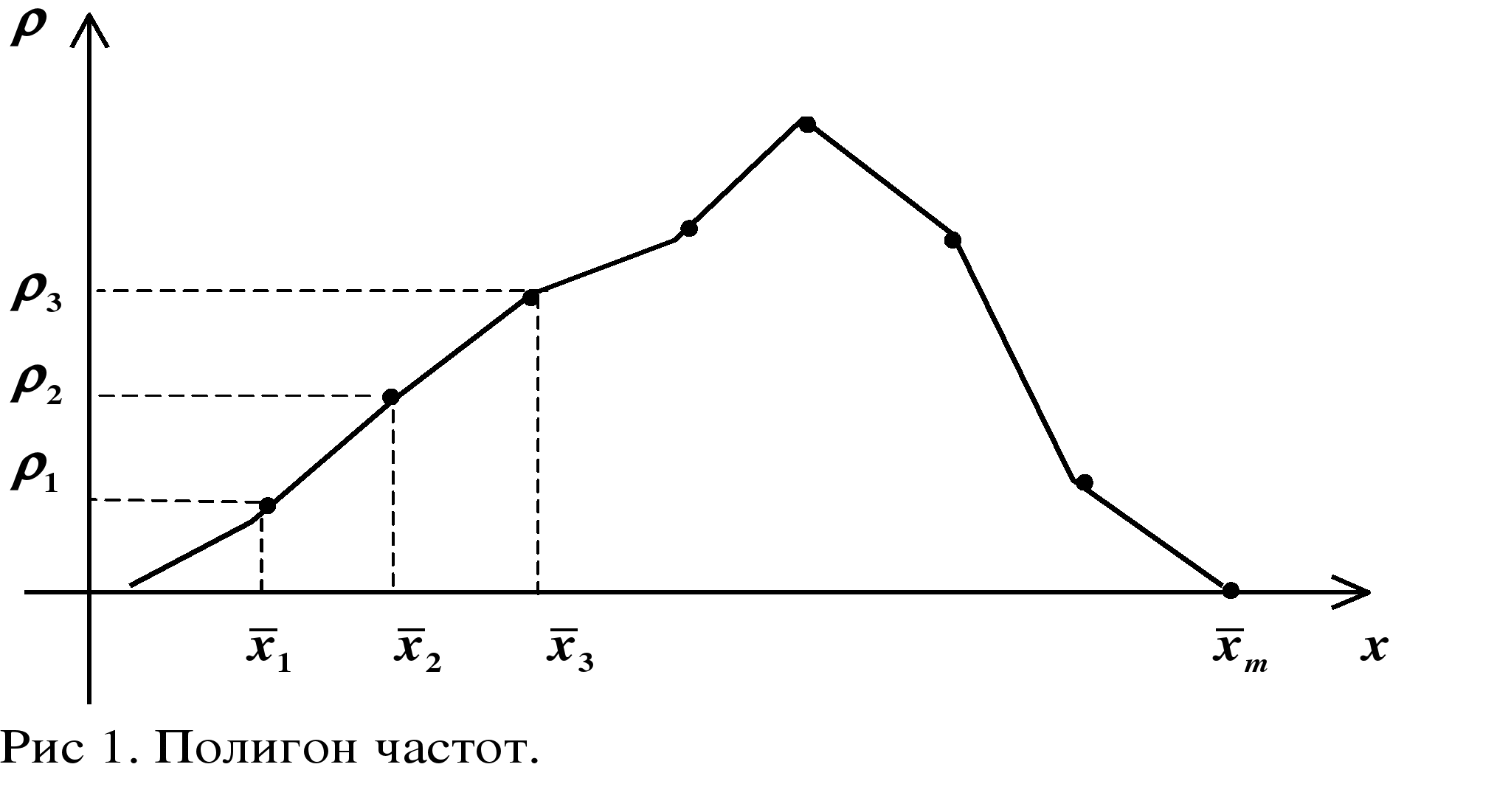
Гистограмма частот – фигура, соединяющая прямоугольники, построенные на одной прямой, основания которых одинаковы.
-
Понятия неориентированного и ориентированного графов. Способы задания графа.
Ответ:
Граф – совокупность ребер и вершин.
Ориентированные – это граф, ребра (дуги) которого имеют направление.
Неориентированные - это граф, ребра (дуги) которого не имеют направление.
Графы у которых начало и конец ребра совпадают с одной и той же вершиной называются графами с петлей.
Нулевой граф – это граф, в котором все вершины не соединяются между собой.
Полный граф – это граф, в котором вершины соединяются всеми возможными связями.
Способы задания графов:
-
Перечисление ребер графа с указанием смежных вершин.
-
Матрица смежности - квадратная матрица размером n*n, где n – число вершин, у которой
-
Матрица инцидентности– это матрица размером m*n, где m-число вершин; n-число ребер.