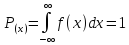5. Понятие схемы Бернулли. Формула Бернулли.

Ответ:

Схема Бернулли – это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие А, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие А появится ровно m раз.

Формула Бернулли:

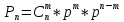
6. Понятие случайной величины. Понятие дискретной случайной величины (ДСВ). Примеры ДСВ. Графическое изображение распределения ДСВ. Математическое ожидание, дисперсия, среднеквадратическое отклонение дискретной случайной величины (ДСВ): определение, сущность, свойства.

Ответ:

Случайная величина – это величина, которая в результате испытания может принимать то или иное числовое значение, причем заранее не известно каким именно будет это значение.

ДСВ – это случайная величина, которая может принимать множество значений, определенных на бесконечной промежутке (x₁, x₂, x₃,…, x_n).

Примеры ДСВ: запись показаний спидометра, измерения температуры в конкретный момент времени.

Функция (закон) распределения ДСВ – это соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями.

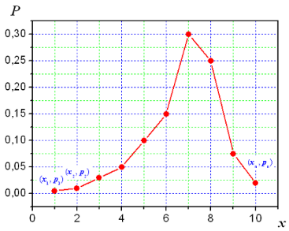
Существует 3 способа записи закона распределения ДСВ:

• Табличный

  

• Графический

• Аналитический

Математическое ожидание ДСВ – сумма произведений всех ее возможных значений на их вероятности.

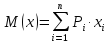
Свойства мат. ожидания ДСВ:

1. M(C) = C

2. M(Cx)=C*M(x)

3. M(x*y)=M(x)*M(y)

4. M(x+y)=M(x)+M(y)

Дисперсия ДСВ – мат. ожидание квадрата отношения случайной величины от квадрата ее мат. ожидания.

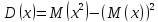
СКО - показатель рассеивания значений случайной величины относительно её математического ожидания.

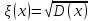
Свойства дисперсии ДСВ:

1. D(C) = 0

2. D(Cx)=C²*D(x)

3. D(x*y)=D(x)*D(y)

4. D(x+y)=D(x)+D(y)

7. Понятие биномиального распределения, характеристики биноминального определения. Вычисление вероятности для биномиального распределения. Его характеристики.

Ответ:

Биномиальный закон – закон распределения ДСВ х, т.е. числа появления события в испытаниях, в каждом из которых вероятность события Р – постоянная величина, причем ее вероятность вычисляется по формуле Бернулли.

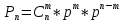
Математическое ожидание:

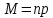
Дисперсия:

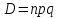
СКО: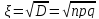

8. Понятие геометрического распределения, характеристики геометрического распределения. Вычисление вероятности для геометрического распределения. Его характеристики.

Ответ:

Геометрическое распределение используется в случае, когда эксперимент осуществляется до первого появления успешного события А.

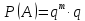
Вероятность Р(А) для всех значений m образует геометрическую прогрессию, поэтому такое распределение называется геометрическим.

Математическое ожидание:

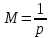
Дисперсия:

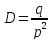
СКО: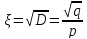

9. Понятие непрерывной случайной величины (нсв). Примеры нсв. Виды нсв. Вероятность события для нсв.

Ответ:

Непрерывная случайная величина – это случайная величина, которая может принимать значение из некоторого бесконечного промежутка.

Примеры НСВ:

1. величина износа детали после некоторого периода эксплуатации;

2. отклонение от цели по дальности точки падения снаряда;

3. изменение напряжения в энергосистеме за определенный промежуток времени.

Виды НСВ:

1. Равномернораспределённая НСВ;

2. Экспоненциальнораспределенная НСВ;

3. Нормальное распределение.

Вероятность события для НСВ