58. Производные тригонометрических и обратных тригонометрических функций

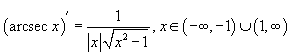
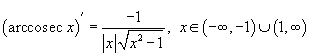
Докажем (1)

y=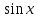

x y=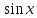

x+△x y=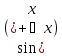

△y=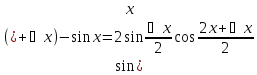

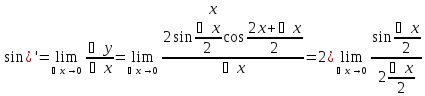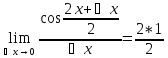(**1*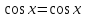

(

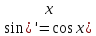
59. Логарифмическое дифференцирование.

Опр: Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.

1. у=

y=

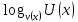
2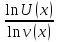. y=U(x)^v(x)

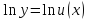
дифференцируем

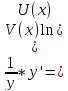
y'=y(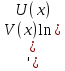

Пример: Найти производную функции у=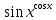

Прологарифмируем обе части и затем продифференцируем:

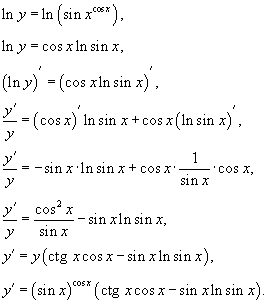
3. Сложная иррациональная функция

Пример: Продифференцировать у(х)=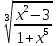

Сначала возьмем логарифм от обеих частей:

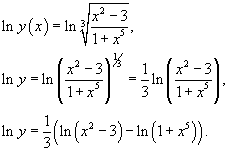
Дифференцируя левую и правую части соотношения, получаем

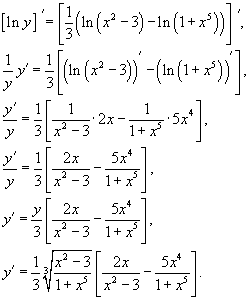
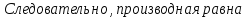
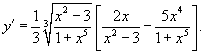
60. Производные неявных и параметрических заданных функций. Производные высших порядков. Механический смысл производной второго порядка.

Производная функции, заданная параметрически

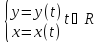
y_x'=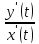

Пример:

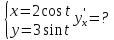
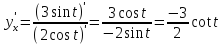
Дифференцирование неявных функций

F(x, y)=0

Пример:

х³-х²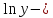х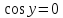

-

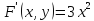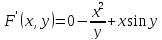
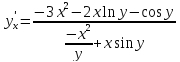
Опр: Производной 2-го порядка(2-ой производной) называют производную от производной.

Обозначение: у^'', (у^')^', f^''(x),

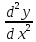
f^'''=(f^'')^'

f⁽⁴⁾

f⁽ⁿ⁾-производная n-ого порядка

Механический смысл производной второго порядка: производная второго порядка есть ускорение.

S^'(t)=V(t)

S^''(t)=V^'(t)=a(t)

61. Дифференциал функции и его связь с производной. Основные свойства дифференциала, инвариантность его формы. Геометрический смысл дифференциала

Здесь ∆x – приращение аргумента x, а ∆y=f(x+∆x)-f(x) – соответствующее приращение функции y.

Будем считать, что данная функция y=f(x) дифференцируема в рассматриваемой фиксированной точке x. То есть будем считать, что производная y′=f′(x) в этой точке существует и конечна. Тогда, согласно (5.1),

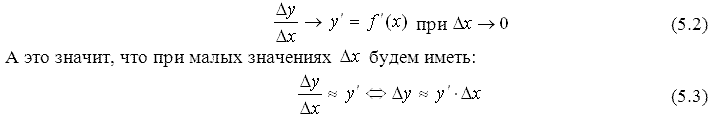
Причем приближенные равенства (5.3) будут тем точнее, чем меньше ∆x (и соответственно чем меньше ∆y).

А теперь будем считать приращение ∆x аргумента функции y=f(x) не просто малым, а бесконечно малым, и назовем его дифференциалом аргумента x. Введем (следуя Лейбницу) для него и специальное обозначение:

dx – дифференциал аргумента x. (5.4)

Таким образом, дифференциал dx аргумента x – это бесконечно малое приращение ∆x этого аргумента. Конечно, только что введенное понятие дифференциала переменной x – математическая абстракция (она сродни диаметру точки или толщине линии). Но математика постоянно пользуется абстракциями, поэтому еще одна абстракция пугать нас не должна.

Если приращение ∆x аргумента x бесконечно мало (∆x =dx), то и приращение ∆y функции y тоже будет бесконечно мало. Обозначим его символом dy и будем называть дифференциалом функции y. Так как ∆y=f(x+∆x)-f(x), то

dy=f(x+dx)-f(x) – дифференциал функции y. (5.5)

Если теперь в приближенных равенствах (5.3) заменить малые, но конечные ∆x и ∆y на бесконечно малые dx и dy, то эти равенства станут точными.

Оба равенства (5.6) имеют важный смысл. Первое из них дает выражение производной y′ функции y через отношение дифференциалов dy и dx функции и аргумента. А второе дает выражение дифференциала функции dy через производную функции y′ и дифференциал аргумента dx.

Кстати, если учесть, что y=f(x), то последнее равенство (5.6) можно записать подробнее:

Формулы (5.12) выражают так называемое свойство инвариантности формы дифференциала функции. Согласно этому свойству, дифференциал функции имеет форму произведения производной этой функции на дифференциал ее аргумента независимо от того, является ли ее аргумент независимой переменной (x) или функцией (u) от другого аргумента.

Действительно, если x – независимая переменная, то дифференциал dy функции y, зависящей от x, находится, в соответствии с (5.6), по первой из формул (5.12). Но так как y=y(u(x)) – сложная функция от x, то используя формулу (2.5) для производной сложной функции, получим:

Геометрический смысл дифференциала:

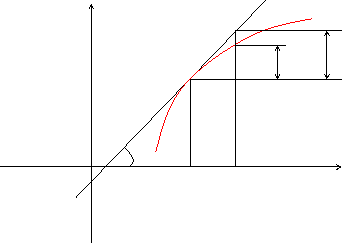
Дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.