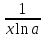54. Производная функция. Ее механический и геометрический смысл. Уравнение касательной.

Пусть у=f(x) непрерывная на промежутке Х

х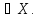

Дадим х приращение △х.

Функция будет иметь приращение △у=f(x+△x)-f(x)

Опр: (*)

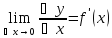Обозначение: у', f'(x),

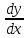
Замечание:

1. При нахождении предела (*) х рассматривается как постоянная.

2. Функция у=f(x) называется дифференцируемой в точке х, если она имеет производную в точке х.

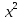Пример: у= у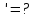

х у=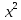

х+△х у=(х+△х)²⁼х²+2х△х+△х²

△у=х²+2х△х+△х²-х²=2х△х+△х²

f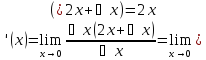

(х²)'=2х

Механический смысл производной:

Прямолинейное движение

S △S

t=0 t t+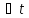

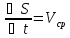
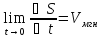
S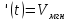

Производная - есть скорость изменения функции

Геометрический смысл:

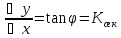
Пусть 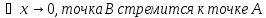, тогда секущая стремится к касательной

f'(x)=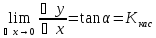

Производная функции у=f(x) в точке х₀ равна угловому коэффициенту касательной, проведенной к графику функции у=f(x) в точке (х₀, f(x₀))

y-y₀=k(x-x₀)

y=y₀+k(x-x₀)

y=f(x₀)+f'(x₀)(x-x₀) – уравнение касательной

Опр: Нормалью кривой в данной точке называется прямая, проходящая через данную точку перпендикулярно касательной в этой точке.

y=f(x₀)-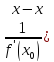₀) – уравнение нормали

55. Дифференцирование. Связь дифференцирования и непрерывности. Основные правила взятия производной.

Опр: Дифференцирование - есть взятие производной.

Т. Если функция дифференцируема в точке х, то она непрерывна в этой точке.

Доказательство.

y=f(x)-дифференцируема

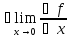
По определению 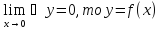-непрерывна в точке х

Найдем

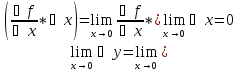
Значит, у=f(x)-непрерывна в точке х

Обратная теорема неверна: если функция непрерывна в точке х, она не обязательно будет дифференцируемой в этой точке.

Пример: у=|х|

D(y)=ℝ, непрерывна на ℝ

х, у=|х|

х+△х, у=|х+△х|

△у=|х+△х|-|х|

у'=

х=0 у'=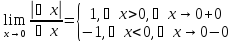

Значит, 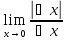не существует, следовательно функция нефифференцируема.

недифференцируемы в точке х

Непрерывность функции является необходимым условием ее дифференцируемости.

Основные правила дифференцирования:

с=const, U=U(x), V=V(x)-непрерывные и дифференцируемые функции на Х

1. (U+V)'=U'+V'

2. (UV)'=U'V+UV'

3. (cV)'=cV'

4. ()'=

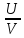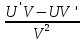
5. c'=0

Докажем (1)

у=U+V

x U(x)+V(x)

x+△x U(x+△x)+V(x+△x)

△(U+V)=U(x+△x)+V(x+△x)-U(x)-V(x)=△U+△V

(U+V)'=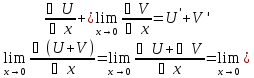

56. Производная сложной и обратной функций.

Производная сложной функции

Пусть y=f(U), U=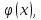тогда y=f(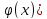-сложная функция

(f(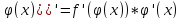

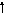
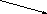
внешняя внутренняя

Доказательство.

y=f(U), U=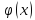

x+△x U=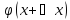

△U=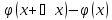

△x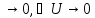

△y=f(U+△U)-f(U)

y_x'=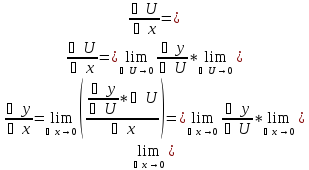f_U'*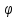x'=f'(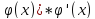

Производная обратной функции

Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).

Теорема. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функция y=f(x) дифференцируема, и

Доказательство.

Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:

Δx=g(y + Δy) − g(y).

Тогда получаем:

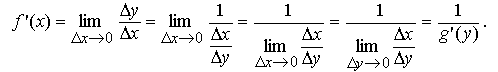
57. Производная функций: у=х, у=, у=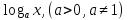

1. y=x, y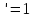

2. y=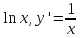

3. у=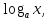y'=