- •41. Экспонента с комплексным показателем. Формула Эйлера. Показательная форма записи комплексного числа (кч). Операции над кч в показательной форме.
- •42. Функция, область определения функции, график функции, способы задания. Понятие неявной, обратной, сложной функции.
- •43. Основные элементарные функции, их свойства и графики
- •44. Тригонометрические и обратно тригонометрические функции, их свойства и графики
- •45. Числовая последовательность, ограниченность, монотонность, предел последовательности, свойства
- •46. Предел функции. Теоремы о существовании пределов
- •47. Бесконечно малые и бесконечно большие функции и их свойства
- •48. Основные теоремы о пределах функций. Теоремы о предельном переходе.
- •49. Первый и второй замечательные пределы. Следствие из 2зп
- •50. Сравнение бесконечно-малых функций. Эквивалентные бмф, их использование.
- •51. Непрерывность функции в точке. Свойства.
- •52.Непрерывность функции на отрезке. Свойства.
- •53. Точки разрыва функции и их классификация
- •54. Производная функция. Ее механический и геометрический смысл. Уравнение касательной.
- •55. Дифференцирование. Связь дифференцирования и непрерывности. Основные правила взятия производной.
- •56. Производная сложной и обратной функций.
- •58. Производные тригонометрических и обратных тригонометрических функций
- •59. Логарифмическое дифференцирование.
- •60. Производные неявных и параметрических заданных функций. Производные высших порядков. Механический смысл производной второго порядка.
- •61. Дифференциал функции и его связь с производной. Основные свойства дифференциала, инвариантность его формы. Геометрический смысл дифференциала
- •62. Применение дифференциала в приближенных вычислениях. Дифференциалы высших порядков, не вариантность их формы.
50. Сравнение бесконечно-малых функций. Эквивалентные бмф, их использование.
Сравнение БМФ
Опр:
Пусть
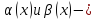 БМФ
при х
БМФ
при х
Если
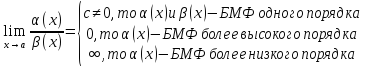
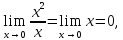 х2-
БМФ более высокого порядка
х2-
БМФ более высокого порядка
Опр:
Если
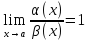 ,
то
,
то
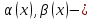 эквивалентные
функции.
эквивалентные
функции.
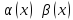
Правила для вычисления пределов:
-
Сумма БМФ при х
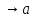 эквивалентна БМФ более низкого порядка
эквивалентна БМФ более низкого порядка -
Сумма ББФ эквивалентна ББФ более высшего порядка
-
Предел отношения 2-ух БМФ равен пределу отношения эквивалентных им функций
Таблица основных эквивалентностей:
sinx
tgx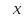
atcsinx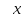
atctgx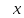
ln(1+x)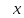
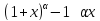
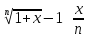
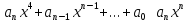
Любой пример.
51. Непрерывность функции в точке. Свойства.
Опр: Функция у=f(x) называется непрерывной в т.х0, если она удовлетворяет следующим условиям:
-
х0
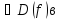 окрестности
т.х0
окрестности
т.х0 -
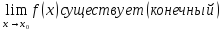
-
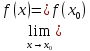
Дадим
х0
приращение
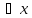
△f=f(x0+△x)-f(x0)
Опр: Функция у=f(x) называется непрерывной в т.х0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
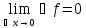
Свойства функций, непрерывных в точке:
Т1. Если f(x) и g(x) непрерывны в т.х0, то
f(x)+g(x)
f(x)*g(x)
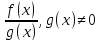
непрерывные функции
Т2.Пусть
у=f(x)
непрерывна в т.х0
и f(x0)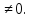 Тогда
знак функции в окрестности т.х0
совпадает со знаком f(x0)
Тогда
знак функции в окрестности т.х0
совпадает со знаком f(x0)
Т3. О непрерывности сложных функций
Если
у=f(U)
непрерывна в т.х0,
а U=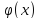 непрерывна в т.х0
(U0=
непрерывна в т.х0
(U0=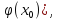 то
сложная функция f(
то
сложная функция f(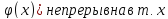 0
0
52.Непрерывность функции на отрезке. Свойства.
Опр: Функция называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого пространства.
Доказано, что все элементарные функции непрерывны на своей области определения. Элементарные функции также непрерывны на области определения.
Свойства функций, непрерывных на промежутке:
Т1. Если у=f(x) непрерывна на [a,b], то она ограниченна на [a,b].
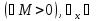 [a,b])
(
[a,b])
(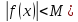
Т2. Теорема Вейерштрасса
Если функция у=f(x) непрерывна на [a,b], то она принимает на этом отрезке наибольшее значение М и наименьшее значение m.
Т3.Теорема Больцано-Каши
Если
у=f(x)
непрерывна на [a,b]
и на концах отрезка принимает значение
разных знаков, то
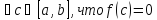
Замечание: Т.Больцано-Каши лежит в основе приблизительного метода решений уравнений f(x)=0
53. Точки разрыва функции и их классификация
Опр: Точкой х0 называется точка разрыва у=f(x), если условие непрерывности в ней не выполняется.
Классификация
точек разрыва
1-го
рода 2-го
рода

точка устранимого точка скачка
разрыва
Опр:
Точной х0
называется точка разрыва 1-го рода, если
односторонние пределы при х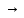 х0
существуют
х0
существуют

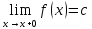
b=c х0-точка устранимого разрыва
b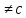 х0-точка
скачка
х0-точка
скачка
Опр: Точка х0 называется точкой разрыва 2-го рода, если хотя бы один из односторонних пределов равен бесконечности или не существует.
Пример:
-
у=
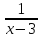
D(y)=
(-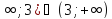
х=3-точка разрыва
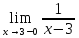 =-
=-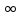
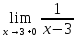 =+
=+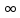
х=3-точка разрыва 2-го рода
-
у=
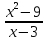
D(y)=(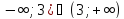
x=3

x=3-точка разрыва 1-го рода, точка устранимого разрыва
у=