
- •41. Экспонента с комплексным показателем. Формула Эйлера. Показательная форма записи комплексного числа (кч). Операции над кч в показательной форме.
- •42. Функция, область определения функции, график функции, способы задания. Понятие неявной, обратной, сложной функции.
- •43. Основные элементарные функции, их свойства и графики
- •44. Тригонометрические и обратно тригонометрические функции, их свойства и графики
- •45. Числовая последовательность, ограниченность, монотонность, предел последовательности, свойства
- •46. Предел функции. Теоремы о существовании пределов
- •47. Бесконечно малые и бесконечно большие функции и их свойства
- •48. Основные теоремы о пределах функций. Теоремы о предельном переходе.
- •49. Первый и второй замечательные пределы. Следствие из 2зп
- •50. Сравнение бесконечно-малых функций. Эквивалентные бмф, их использование.
- •51. Непрерывность функции в точке. Свойства.
- •52.Непрерывность функции на отрезке. Свойства.
- •53. Точки разрыва функции и их классификация
- •54. Производная функция. Ее механический и геометрический смысл. Уравнение касательной.
- •55. Дифференцирование. Связь дифференцирования и непрерывности. Основные правила взятия производной.
- •56. Производная сложной и обратной функций.
- •58. Производные тригонометрических и обратных тригонометрических функций
- •59. Логарифмическое дифференцирование.
- •60. Производные неявных и параметрических заданных функций. Производные высших порядков. Механический смысл производной второго порядка.
- •61. Дифференциал функции и его связь с производной. Основные свойства дифференциала, инвариантность его формы. Геометрический смысл дифференциала
- •62. Применение дифференциала в приближенных вычислениях. Дифференциалы высших порядков, не вариантность их формы.
41. Экспонента с комплексным показателем. Формула Эйлера. Показательная форма записи комплексного числа (кч). Операции над кч в показательной форме.
Показательная и тригонометрическая функции в области КЧ связаны между собой формулой:
еiq= cosq+isinq-формула Эйлера (1).
Пусть КЧ Z в тригонометрической форме имеет вид Z= r (cosq+isinq). Тогда из (1) следует, что z= reiq – показательная форма записи КЧ.
ПРИМЕР: z= -1+i
r=
|z|=
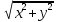 =
=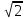 ;
q=argz=
;
q=argz=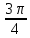
z=
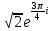 -показательная
форма записи КЧ.
-показательная
форма записи КЧ.
С помощью ф. Эйлера можно определить показательную функцию комплексного аргумента.
Пусть
z=x+iy,
тогда
 Любой
пример.
Любой
пример.
Заменим
в (1) q
на –q.
Получим:
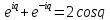 .
Отсюда cosq=
.
Отсюда cosq= .
.
Аналогично,
sinq=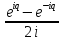 .
(Любой пример)
.
(Любой пример)
Действия над КЧ в показательной форме
Произведение
2-ух КЧ
z1=x1+iy1
, z2=x2+iy2
равно
z1z2=y1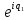 *
y2
*
y2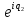 =
y1y2
=
y1y2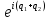 =y1y2
=y1y2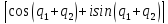 .
.
Деление
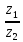 =
=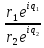 =
=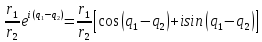
Возведение
в целую положительную степень
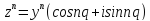 -
ф. Муавра
-
ф. Муавра
Извлечение
корня n-степени
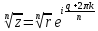
42. Функция, область определения функции, график функции, способы задания. Понятие неявной, обратной, сложной функции.
Опр: Пусть заданы 2 непустых множества X и Y. Если каждому элементу х€Х по правилу f соответствует единственное значение у€У, то говорят, что на множестве Х задана функция f со множеством значений У.
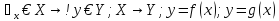
x-независимая переменная
у- зависимая переменная, функция
Х-множество переменных
Х=D(f)- область определения-все те значения х, при которых сосчитана функция
У= Е(f)- область значений
Опр: Графиком функции у=f(x)называют множество точек плоскости Оху с координатами (х, f(x)), где х€D(f)
Способы задания:
-
аналитический явно у=f(x)
неявно F(x,y)=0
кусочный
параметрический
-
табличный
-
графический
Опр: Если у зависит от U, а U зависит от х, то у зависит от х, и называется сложной функцией.
у=f(x), U=g(x)
y=f(g(x))
Опр:
Функция у=f(x)
называется обратимой на Х, если
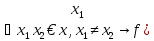 )
)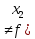 )
)
Опр: Пусть у=f(x) – обратимая функция на Х
Выразим
из формулы у=f(x)
переменную х, получим х=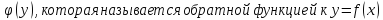
Заменив у на х , х на у, имеем у=f-1(x)
43. Основные элементарные функции, их свойства и графики
Опр:
Функция,
заданная формулой у=ах,
где а>0, а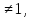 называется
показательной
функцией с
основанием а.
называется
показательной
функцией с
основанием а.
При а=1 имеем график прямой линии, параллельной Ох.
Свойства:
D(y)=
E(y)=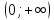
монотонна: возрастает при а>1,
убывает при 0<a<1
неограниченная, непрерывная, непериодическая
Опр:
Функция у=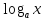 ,
где а>0, а
,
где а>0, а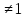 ,
называется логарифмической.
Эта функция является обратной к
показательной функции; ее график может
быть получен поворотом графика у=ах
вокруг биссектрисы 1 координатного
угла.
,
называется логарифмической.
Эта функция является обратной к
показательной функции; ее график может
быть получен поворотом графика у=ах
вокруг биссектрисы 1 координатного
угла.
Свойства:
D(y)=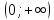
E(y)= ℝ
монотонна: возрастает при а>1
убывает при 0<a<1
неограниченная, непрерывная, непериодическая
Опр: Функция, заданная формулой у=хα, называется степенной функцией, где α-постоянная.
При α=1 получаем прямую, при α=2-квадратную параболу, при α=-1-гиперболу, при α=3-кубическую параболу.
Свойства:
