Расчет статически определимых ферм. Общие понятия.

Ферма это динамичная геометрически неизменяемая система, состоящая из прямых стержней соединенных между собой идеальными шарнирами.

Бывают железобетонные, металлические, деревянные.

Совокупность стержней, ограничивающих ферму сверху, называется верхним поясом (1) , снизу – нижним поясом (2). Внутренние стержни образуют решетку, вертикальные стержни называются стойками (3), наклонные – раскосами (4).

В качестве генеральных размеров ферм принимают:

- длину пролета l – расстояние между опорами

- высоту h – наибольшее расстояние между по вертикали между узлами поясов

- длину панели d – расстояние между узлами верхних или нижних поясов

Оптимальные размеры ферм при .

Классификация ферм.

I. По назначению: - мостовые;

- крановые;

- строительные.

II. По очертанию поясов:

а) с параллельными поясами

б) полигонные

в) треугольные

г) криволинейные

III. По типу решетки:

а) Раскосая решетка с нисходящими и восходящими раскосами.

б) Треугольная решетка.

в) Полураскосая (применяют при высоких фермах)

г) Шпренгельная.

IV Сложные:

а) с консолями

б) многопролетные

Расчет простых ферм. Понятие о расчетной схеме фермы.

Наиболее простой расчетной схемой фермы является стержневая конструкция, в которой все стержни соединены в узлах идеальными шарнирами, а нагрузки в виде сосредоточенных сил приложены только в узлах. В стержнях фермы возникают только продольные усилия, а изгибающие моменты и перерезывающие силы равны нулю.

Расчет фермы заключается в определении расчетных продольных усилий в стержнях от действия расчетных нагрузок.

Определение опорных реакций.

Для определения опорных реакций используем уравнение статики:

∑M_A = 0 =>V_B

∑M_B = 0 => V_A

Проверка: ∑Y = 0

Предварительно всю внешнюю нагрузку нужно привести к узловой и распределить ее между верхним и нижним поясами фермы.

Пример.

1. Заданную распределенную нагрузку приводим к погонной:

q_n = q*в=4*6=24 кН/м

в – расстояние между фермами.

2. Распределяем погонную нагрузку на узловую:

Р_узл = q_n*d=24*2=48 кН

Р_{узл крайн} = 0,5Р_узл=24 кН

3. Распределяем нагрузку на верхние и нижние узлы:

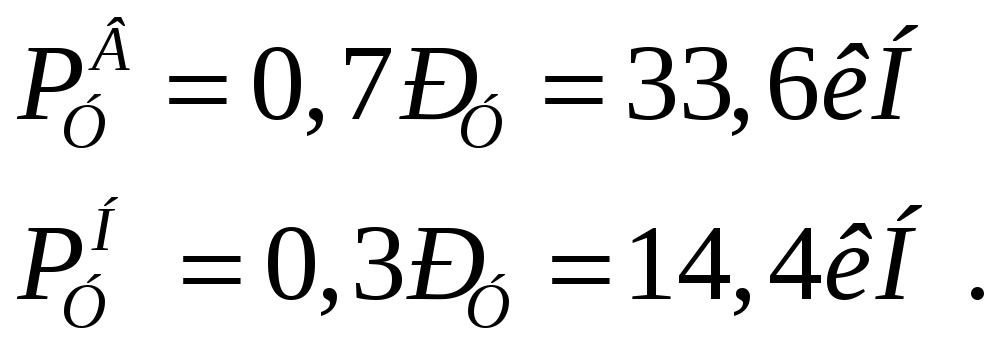
4. Определяем опорные реакции.

Проверка:

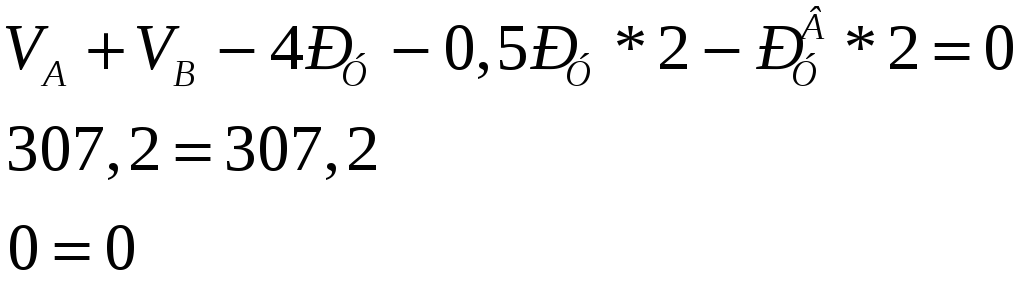
Определение усилий в стержнях фермы аналитическим способом.

Этот способ основан на рассмотрении равновесия отсеченной части фермы и использовании различных видов уравнений равновесия.

При проведении сечений нужно помнить, что:

- сечение должно разделить ферму на две части;

- сечение, как правило, должно проходить не более чем через три стержня.

Существует 4 аналитических способа:

а) способ моментных точек;

б) способ проекций;

в) способ вырезания узлов;

г) способ замены стержней (для сложных ферм).

Способ моментных точек (способ Риттара).

Применяется в тех случаях, когда при рассечении фермы на две части разрезаются 3 стержня с неизвестными усилиями, не сходящиеся в одной точке. Если при определении усилий в одном из стержней 2 других стержня не параллельны между собой, то точка их пересечения является моментной для искомого усилия. Этот способ и способ проекций позволяют определять усилия в стержнях ферм независимо от усилий в соседних стержнях, так как соответствующие уравнения равновесия содержат всего одно неизвестное.

Разрезаем ферму сечением к-к. Отбрасываем правую часть. Взамен показываем усилия в стержнях, считая их растягивающими. А – моментная точка для усилия N₁

О – моментная точка для усилия N₃

Составляем уравнения равновесия:

- сжат.

Замечание:

- из геометрических соображений.

Достоинства: удобен, универсален, можно найти усилия в любом стержне.