§ 4 Элементы аналитической геометрии на плоскости

Прямая линия.

Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у

Ах + Ву + С =0,

где А и В одновременно не равны нулю, определяют прямую в этой системе координат.

Уравнение прямой с угловым коэффициентом: ,

где - угловой коэффициент, α – угол наклона прямой к положительному направлению оси ОХ, - величина отрезка, отсекаемого на оси ОУ.

- уравнение пучка прямых, проходящих через точку М₀(х₀;у₀).

- уравнение прямой, проходящей через две точки М₁(х₁;у₁), М₂(х₂;у₂).

Пусть даны две прямые:

у=к₁ х+в₁ общее уравнение А₁х + В₁у +С₁ = 0

у=к₂х + в₂ общее уравнение А₂х +В₂у + С₂ = 0.

Угол между данными прямыми определяется по формуле

.

Условие параллельности прямых:

Две прямые параллельны, если их угловые коэффициенты равны, коэффициенты при переменных общих уравнений пропорциональны

т.е.

Условие перпендикулярности прямых:

Две прямые перпендикулярны, если их угловые коэффициенты обратны по значению и противоположны по знаку, сумма произведений коэффициентов при переменных общих уравнений равна нулю т.е.

.

Расстояние от точки до прямой.

Пусть на плоскости заданы точка М₀(х₀;у₀ ) и прямая Ах + Ву + С = 0. Под расстояни­ем от точки М₀ до прямой Ах + Ву + С = 0 при­нимается длина перпендикуляра, опущенного из точки М₀ на прямую. Данное расстояние можно определить по формуле:

Пример: Даны вершины А(2; 1), В(6; 3), С(4; 5) треугольника.

Найти:

1. уравнение и длину стороны АВ;

2. уравнение высоты, проведенной из вершины С;

3. уравнение медианы, проведенной через вершину С;

4. длину высоты, опущенной из вершины С;

5. величину внутреннего угла А;

6. площадь треугольника АВС.

Сделать чертеж.

Решение.

Сделаем чертеж :

y

C

B

D

A

M

x

9

1) Длину стороны АВ находим как расстояние между двумя точками

А и В.

.

Уравнение прямой АВ найдем по формуле уравнения прямой проходящей через две точки.

.

2) Уравнение высоты, проведенной из вершины С можно найти по формуле уравнения пучка прямых, проходящих через данную точку и так как СD перпендикулярно АВ а угловой коэффициент АВ можно найти .

Тогда у – 5 = - 2(х - 4), или 2х + у – 13 = 0.

3) Для определения уравнения медианы СМ найдем координаты точки М, которая делит отрезок АВ пополам

Медиана СМ проходит через две точки С(4; 5) и М(4; 2). Так как абсциссы этих точек равны можно сделать вывод, что прямая СМ параллельна оси ОУ и ее уравнение имеет вид х = 4.

4. Чтобы найти длину высоты, опущенной из вершины С, воспользуемся формулой расстояния от точки до прямой. Уравнение прямой АВ имеет вид х – 2у = 0, С(4; 5).

.

5) Величину внутреннего угла А найдем как угол между двумя прямыми АС и АВ. Уравнение прямой АВ известно, оно имеет вид х – 2у = 0. Составим уравнение прямой АС, воспользуемся формулой уравнения прямой, проходящей через две точки: .

.

6) Чтобы найти площадь треугольника воспользуемся формулой 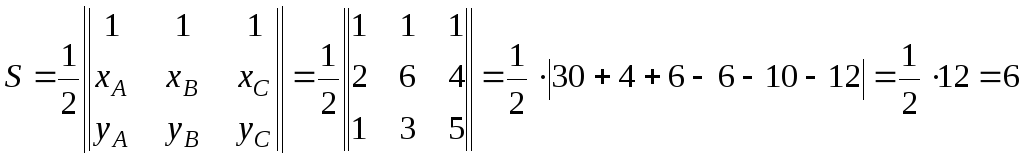2.3 Варианты контрольной работы 1

Вариант 1

1. Выполнить действия над матрицами:

D=(A×B-3E)^T+2C, если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

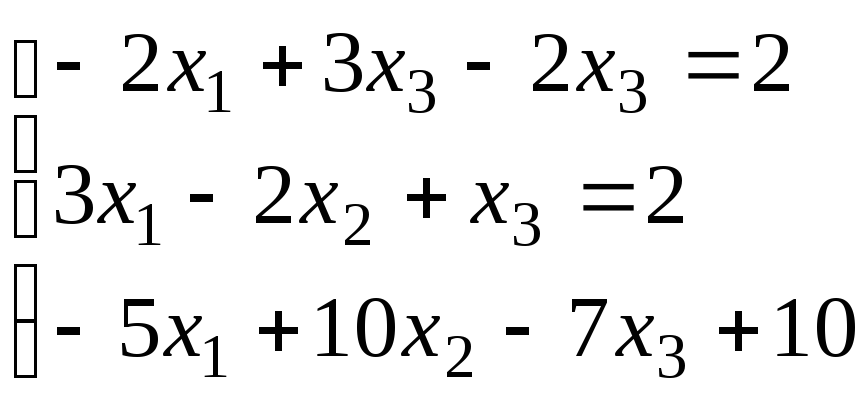
5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей .

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(3;3), В(-9;12), С(-7;-2).

Вариант 2.

1. Выполнить действия над матрицами:

D=A×B^T-2E+C² если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность.

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(5;1), В(-7;10),С(-5;-4).

Вариант 3.

1. Выполнить действия над матрицами:

D=(A×B-3E)^T+2C, если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(2;-1), В(-10;8), С(-8;-6).

Вариант 4.

1. Выполнить действия над матрицами:

D=(A×B)^T-2E+C² если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(6;2), В(-6;11), С(-4;-3).

Вариант 5.

1. Выполнить действия над матрицами:

D=(A×B-3E)^T+2C, если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(8;-2), В(-4;7), С(-2;-7).

Вариант 6.

1. Выполнить действия над матрицами:

D=A×B^T-2E+C² если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность.

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(1;1), В(-11;10), С(-9;-4).

Вариант 7.

1. Выполнить действия над матрицами:

D=(A×B-3E)^T+2C, если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей.

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

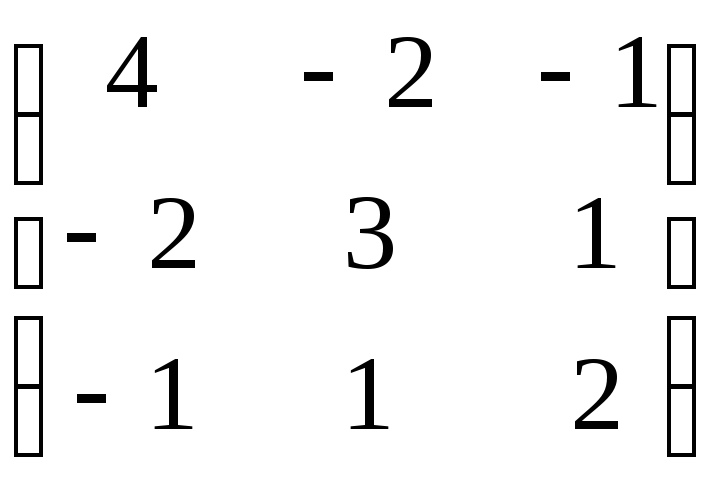7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(4;-3), В(-8;6), С(-6;-8).

Вариант 8.

1. Выполнить действия над матрицами:

D=A×B^T-2E+C² если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей .

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(0;1), В(-12;10), С(-10;4).

Вариант 9.

1. Выполнить действия над матрицами:

D=(A×B-3E)^T+2C, если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей .

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(3;0), В(-9;9), С(-7;-5).

Вариант 10.

1. Выполнить действия над матрицами:

D=A×B^T-2E+C² если

2. Вычислить определитель:

3.Решить систему:

а) методом обратной матрицы;

б) по формулам Крамера;

в) методом Гаусса.

4.Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

5. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей .

6. Запишите квадратичную форму, заданной матрицей, исследовать ее на знакоопределенность .

7. Даны координаты вершин треугольника АВС. Найти:

1) уравнение стороны АВ;

2) длину стороны АВ;

3) уравнение и длину высоты СК;

4) уравнение медианы АМ;

5) величину угла САВ;

6) площадь треугольника АВС;

7) сделать чертеж в прямоугольной системе координат, если

А(-6; 1), В(6; 10), С(4;-4).