2.4 Метод Гаусса.

Рассмотрим решение системы методом Гаусса на конкретном примере:

Метод Гаусса заключается в том, что с помощью элементарных преобразований система приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних, находятся все остальные.

Составим расширенную матрицу из коэффициентов при переменных и свободных членов, поменяв первую и вторую строку, чтобы а₁₁=1

Умножим элементы первой строки на -2 и прибавим к соответствующим элементам второй строки, умножим элементы первой строки на -7 и прибавим к соответствующим элементам третьей строки. В результате получим в первом столбце, во второй и третьей строке 0

Умножим элементы второй строки на -9 а элементы третьей на 5 и полученные элементы второй строки прибавим к соответствующим элементам третьей строки, тогда получим:

Запишем преобразованные уравнения:

Теперь можно найти значения переменных, подставляя последовательно значение х₃ во второе уравнение, найдем х₂, подставим значения х₂ и х₃ в первое уравнение найдем х₁

Ответ: (1;1;1)

2.4 (а) Методом Гаусса решить систему линейных уравнений и найти одно из базисных решений:

Решение:

Составим расширенную матрицу и с помощью элементарных преобразований приведем её к ступенчатому виду.

r(A)=2, число переменных n=4, следовательно система имеет бесконечное множество решений.

Определитель при переменных х₁ и х₂ , следовательно их можно взять за основные. Остальные, неосновные переменные х₃ и х₄ переносим в правые части уравнений:

Нашли общее решение системы. Чтобы найти базисное решение приравняем свободные переменные нулю, т.е.х₃=х₄=0. Получим базисное решение (-9;5; 0;0)

§ 3 Элементы векторной алгебры

3.1 Определения и основные понятия

Вектором называется направленный отрезок, он обозначается двумя буквами или одной .

Векторы называются коллинеарными, если они лежат на одной прямой, или на параллельных прямых.

Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Координатами вектора в декартовом базисе называются его проекции на оси координат. Обозначим координаты вектора через х, у,z получим следующее представление вектора в координатной форме:

В координатной форме сокращенно вектор можно записывать следующим образом .

Если вектор задан координатами начала и конца М₁(х₁,у₁,z₁) и М₂(х₂,у₂,z₂), то координаты вектора = (х₂ – х₁,у₂ – у₁, z₂ - z₁).

Длина вектора (модуль) находится по формуле:

.

3.2 Действия над векторами

Если векторы и заданы координатами, то сумму и разность векторов, произведение вектора на число можно найти по формулам:

При умножении вектора на число получаем вектор коллинеарный данному, следовательно, можно сделать вывод:

Условием коллинеарности двух векторов является пропорциональность их координат.

Скалярным произведением двух векторов называется произведение их модулей, умноженное на косинус угла между ними .

Если векторы заданы координатами, то .

С помощью скалярного произведения можно определить угол между векторами: .

Векторы перпендикулярны если их скалярное произведение равно

нулю .

Векторным произведением двух векторов и называется вектор , определяемый следующими условиями:

1. вектор перпендикулярен векторам и ;

2. вектор имеет длину, численно равную площади параллелограмма, построенного на векторах а и в как на сторонах

3. векторы а,в,с образуют правую тройку.

z

Е

x

y

O

сли векторы и заданы координатами,

то

Согласно определению, площадь параллелограмма, построенного на векторах и , равна модулю их векторного произведения: , где S_Δ – площадь треугольника, построенного на векторах и .

3.3 Пример: Найти площадь треугольника, построенного на векторах и угол между ними.

Чтобы найти площадь треугольника, найдем векторное произведение векторов и

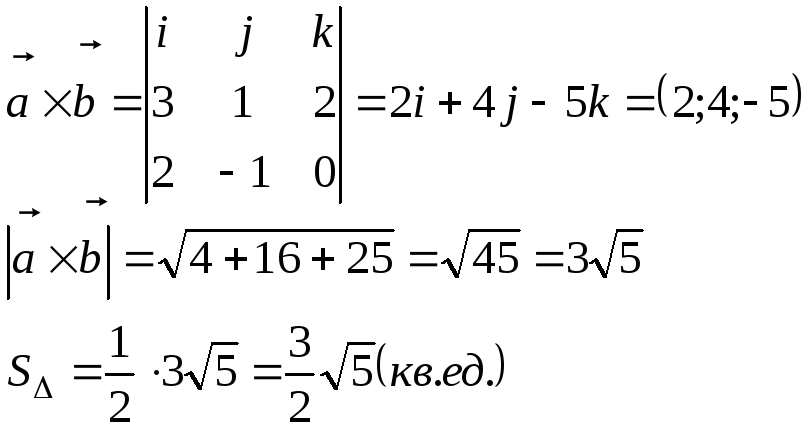
Чтобы найти угол между двумя векторами, воспользуемся формулой:

.