Добавил:

student_tipo Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балаковский институт техники, технологии и управления

Предмет:

Локальные системы управления

Файл:

Курсовые работы / дозирование сыпучих компонентов при замесе теста / основная часть.docx

Скачиваний:

Добавлен:

23.02.2014

Размер:

397.6 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

ВВЕДЕНИЕ

Бурное развитие автоматики, электроники и вычислительной техники привело к внедрению автоматики буквально во все области деятельности человека. Автоматика и автоматизация стали главным направлением развития всей техники. Совершается переход от автоматизации отдельных простейших производственных операций к комплексной автоматизации средств производства и производственных процессов.

Роль человека при этом сводится к организации работы автоматических систем и средств вычислительной техники. Такому их проектированию, соединению и использованию, которое обеспечивает получение необходимых результатов с наименьшими затратами.

Локальные системы управления - это автоматические модули, используемые для решения одной функциональной задачи, для управления одним устройством, для регулирования или сигнализации одного параметра.

Процесс управления состоит из следующих четырех этапов:

1. Получение информации о результатах управления.

2. Анализ полученной информации.

3. Выработка решения и исполнение решения. т. е. осуществление управляющих действий.

Типичными элементами любой системы управления являются измерители различных физических величин, или датчики, вводящие в систему управления информацию о задачах управления и результатах управления, функциональные преобразователи или вычислительные устройства, осуществляющие определение параметров управления и заданное их преобразование или более сложный анализ информации и вырабатывающие сигналы управления, исполнительные устройства.

C усложнением задач автоматического управления становятся все более сложными и системы управления. Но, чем сложнее система, чем большее число элементов она содержит, тем более вероятны ее отказы из-за выхода из строя отдельных элементов.

Отыскание неисправных элементов в сложных системах представляет собой весъма сложную задачу и требует много времени. И чем сложнее система, тем труднее найти в ней причину отказа и выявить отказавший элемент. Поэтому для нормального функционирования сложной системой управления, для ее нормальной эксплуатации необходимо автоматизировать контроль состояния всех ее частей. Эту задачу наиболее целесообразно решать путем ввода в саму структуру системы, наряду с перечисленными основными элементами, соответствующих приборов и устройств для автоматического контроля состояния системы и режима работы всех ее элементов, а также для сигнализации о неисправности и указания неисправных элементов.

1 РАСШИРЕННОЕ ТЕХНИЧЕСКОЕ ЗАДАНИЕ

1.1 Назначение ЛСАУ

Дозатор сыпучих компонентов Х120 (Автомукомер) с микропроцессорным управлением - современный весовой измерительный комплекс с автоматической разгрузкой бункера. Предназначен для порционного взвешивания муки и других сыпучих продуктов.

Дозатора Х110 обеспечивает:

-Взвешивание и цифровой отсчет продуктов посредством тензодатчиков;

-Дозированный набор одного сорта или последовательно двух или трех продуктов;

-Электронное управление приводом разгрузочного устройства;

-Учёт количества отпущенных через дозатор продуктов в текущую смену, предыдущую смену и тотальный с начала эксплуатации. Учёт производится отдельно по сортам.

-Память рецептуры до 90 сортов смесей;

-Возможность комплектования различными разгрузочными устройствами (поворотная заслонка, пережимное разгрузочное устройство, поворотное или двухстороннее разгрузочное устройство)

-Для обеспечения "валки" муки в дозаторе предусмотрена опция - разбиение загрузок бункера. Принцип разбиения заключается в автоматическом делении дозы каждого продукта на две или три равные части, которые последовательно и циклически загружаются в бункер.

1.2 Состав локального системного управления :

1)Шкаф управления - служит для автоматического управления дозаторной установки .

2)Усилитель – усиливает входное напряжение .

3)Реле – коммутационное устройство.

4)Привод электромагнитный - основан на взаимодейстии магнитного поля катушки с подвижным ферромагнитным сердечником.

5)Тензометрический датчик – основан на преобразовании механической деформации, возникающей при нагрузке датчика, в электрический сигнал.

Рисунок 1- Дозатор Х110

1.3 Технические характеристики

Номинальные величины порций, кг 10 ÷ 100

Дискретность изменения величины веса, кг 0,1

Предельно допустимое отклонение веса ± (0,4% +0,1 кг)

Емкость бункера номинальная, кг 100 (0,24 м³)

Напряжение питающей сети с частотой 50 Гц, В 198 ÷ 242

Потребляемая мощность, кВт, не более 0,1

Габаритные размеры, мм:

- Шкаф управления Х-32/110 300 х 400 х 150

- Бункер с рамой 1020 х 1000 х 1120

- Изделие в упаковке, мм 1060 х 1110 х 1700

Масса в упаковке не более, кг 105

1.4 Требования надежности системы

Время регулирования t_p= 30 с

Период дискретизации T₀= 0,5 1/с

Перерегулирование σ = 45%

2 ВЫБОР И ОБОСНОВАНИЕ ВЫБОРА ЭЛЕМЕНТНОЙ БАЗЫ

ЛОКАЛЬНОЙ СИСТЕМЫ УПРАВЛЕНИЯ

2.1 Элементный синтез

Структурная схема системы автоматического регулирования дозирования представлена на рисунке 2.

МП-микропроцессор

У-усилитель

Р-реле

ПЭМ- Привод электромагнитный

Д- тензометрический датчик

Рисунок 2 - Функциональная схема системы автоматического управления дозирования компонентов при замесе хлеба

2.2 Выбор микроконтроллера

Для разрабатываемой системы автоматического регулирования выбираем микроконтроллер, исходя из технических характеристик и экономической эффективности, ZNEO Z16F.

Серия ZNEO Z16F - 16-разрядные микроконтроллеры с однотактовой системой команд, скорость 20 MIPS при частоте 20 МГц.

Z16F представляет собой весьма мощное решение, включающее большой объём внутренней flash-памяти без тактов задержки, широкий набор встроенных математических операций, 32-разярядное АЛУ с поддержкой 8-, 16- и 32-разрядных операций, поддержку умножения слов 32х32 и деления слов 64х32, 16-битную внешнюю шину. Широкий набор периферии и аналоговых блоков позволяет использовать ZNEO в самых различных приложениях.

Характеристики микроконтроллера:

ЦПУ ZNEO 20 МГц;
До 128 Кбайт Flash ПЗУ с 16-разрядным доступом и внутренней перезаписью;
До 4 Кбайт ОЗУ с 16-разрядным доступом;
Интерфейс внешней памяти;
АЦП 10 бит, 12 каналов;
Операционный усилитель;
Аналоговый компаратор;
4-канальный контроллер прямого доступа к памяти;
Два полнодуплексных UART с поддержкой LIN и IrDA;
Генератор импульсов;
I2C master/slave контроллер;
ESPI контроллер;
Скорость выполнения команд - до 20 MIPS;
Рязрядность внутренней и внешней шины 16 бит;
ШИМ-модуль 12-бит;
Три стандартных таймера 16-бит;
До 76 линий ввода/вывода;
До 24 прерываний;
1-pin для внутренней отладки;
Рабочие температурные диапазоны - [0;+70], [-40;+105] и [-40;+125]C.

Передаточная функция микроконтроллера:

W_мп(p) = 1.

2.3 Выбор усилителя

Применяем транзисторный усилитель. Электронные усилители обладают малым запаздыванием, т.е. являются практически безинерциоными. Передаточная функция усилителя имеет вид:

₍₁₎

Определим коэффициент :

Коэффициент k_у определяется как отношение мощности выходного сигнала устройства к мощности входного:

, (2)

где U_вых -выходное напряжение необходимое для срабатывание реле U_вых=

=12В

U_вх- напряжение на выходе МК U_вх =5В ;

Следовательно передаточная функция усилителя:

2.4Выбор реле

В данной системе выбирается промежуточное реле постоянного тока ПЭ-39М.

Технические характеристики:

-потребляемая мощность, Вт 1

-время срабатывания не более, сек 0,015

-номинальный ток контактов, А 8

-напряжение питания, В 12

-напряжение срабатывания Uср, В 12

Статическая характеристика реле представлена на рисунке 3.

F(x)

-b

Рисунок 3 - Статическая характеристика реле

Для данного вида нелинейности передаточная функция клапана находится по формуле /7, с. 157/:

=, (3)

где Кр –коэффициент передачи реле,

А – амплитуда первой гармоники сигнала,

В – значение напряжения срабатывания.

Таким образом, значение передаточной функции будет иметь вид::

W_р(р) = 1,2.

2.5 Выбор электромагнитного привода

Электромагниты типа ПЭ-35ГМ предназначены для управления гидрораспределителями (ДУ 6мм.), пневматическими клапанами и другими механизмами.

Электромагниты рассчитаны на включение в сеть постоянного и переменного тока. Магниты герметичные с улучшенной технической характеристикой, заменяют электромагниты ЭМ-24 и ПЭ-35. Климатическое исполнение УХЛ4, ХЛ1, Т3 по ГОСТ 15150. Степень защиты IP54, IP65 в зависимости от исполнения электрического соединителя по ГОСТ 14254. Выводы катушки выполняются соединителем электрическим СЭ11-19 или с соединителем 2РМГ.

Технические данные:

- Тяговое усилие при номинальном ходе якоря, Н 50

-ход не более, 12

- режим работы повторно-кратковременный

-тип электромагнита толкающий

- время срабатывания, с, не более 0,04

-масса электромагнита, кг 0,5

Рисунок 4 – Привод электрмагнитный ПЭ-35ГМ

Передаточная функция /7, с. 47/:

, (4)

где -передаточный коэффициент соленоида,

-постоянная времени соленоида,

-коэффициент демпфирования соленоида.

, (5)

где R₀ и L₀– активное сопротивление и индуктивность катушки, соответству-щее начальному положению якоря;

, (6)

где k₀ – коэффициент пропорциональности между силой электромагнита и током управления I_у в катушке;

, (7)

где k_д -коэффициент демпфирования, k_п – жесткость пружины.

Таким образом, получим:

Выбор тензодатчика.
После проведенного анализа датчиков, исходя из технического задания и параметров системы, в качестве датчика обратной связи был выбран тензодатчик модификации STC. Он предназначен для непрерывного преобразования давления (силы) в электрический выходной сигнал.

Технические характеристики:

Номинальная нагрузка 30, 50, 75, 100 кг

Рабочий коэффициент передачи 3мВ/В

Класс точности 0,02%

Рабочий диапазон температур С -20…+60

Число поверочных интервалов 3000

Темп. коэфф. чувствительности % / 10^oС <=±0,0110

Темп. коэфф. нуля % / 10^oС <=±0,0168

Гистерезис %D <=±0,0167

Нелинейность %D <=±0,016

Входное сопротивление 385 ± 5 Ом

Выходное сопротивление 350 ± 3 Ом

Напряжение питания 2…10 В

Предельная нагрузка % Dmax 150

Передаточная функция тензорезисторного датчика имеет вид:

, (8)

где к_к – передаточный коэффициент датчика

Т_к – постоянная времени датчика

Выходное напряжение датчика равно 10 В. Масса одной порции дозируемого материала составляет 30 кг. Рассчитаем коэффициенты.

; (9)

с. (10)

Таким образом, передаточная функция датчика будет иметь вид:

3 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ САУ

3.1 Расчет передаточной функции неизменяемой части системы и проверка на устойчивость

Передаточные функции элементов:

W_мп(p) = 1.

W_р(р) = 1,2.

Передаточная функция замкнутой системы:

(11)

Оценим устойчивость системы. Оценку устойчивости проведем по критерию устойчивости Гурвица. Для этого рассмотрим характеристическое уравнение замкнутой системы:

Обозначим:

Необходимое условие устойчивости выполнено - все коэффициенты характеристического уравнения положительные.

Составим определители Гурвица:

(12)

(13)

(14)

Так как все определители Гурвица положительные, то выполняется и достаточное условие устойчивости системы. Таким образом, система устойчива.

Чтобы определить показатели качества, строится график переходного процесса. Для этого находится обратное преобразование Лапласа от передаточной функции замкнутой системы.

Рисунок 7 – Переходный процесс системы

По графику переходного процесса определим показатели качества системы:

1) Время регулирования (время переходного процесса) – это величина, характеризующая быстродействие системы и определяется величиной

h_уст = 3

∆= 5%(h_уст) = 0,925

Время регулирования t_р= 10 с

2) Перерегулирование (максимальная динамическая ошибка) – это величина, которая определяет максимальное отклонение регулируемой величины от установившегося значения, выраженная в процентах:

(15)

3) Время нарастания регулируемой величины – это время от момента приложения сигнала до того момента, когда выходная величина достигнет своего максимального значения.

Время достижения максимума (время нарастания) t_н = 0,35 с

4) время первого согласования – это время, когда регулируемая величина первый раз достигает своего установившегося состояния.

t_c=0,1 с

Показатели качества управления удовлетворяют требованиям, заданным в техническом задании. Построим график АЧХ для определения колебательности системы:

Приведем передаточную функцию к частотному виду:

Выделим действительную и мнимую части:

Определим вид частотной функции:

Рисунок 8 - Амплитудно-частотная характеристика

Из построенной АЧХ определяется косвенные оценки качества системы:

резонансная частота – определяется как частота в которой АЧХ достигает своего максимального значения .
показатель колебательности – определяется как отношение амплитуд:

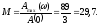
частота среза – при которой АЧХ достигает значения равного 1:

полоса пропускания (частота при ):

3.2 Расчет передаточной функции системы с учетом микропроцессора и проверка ее на устойчивость

Разрабатываемая система является дискретной, поэтому, чтобы провести ее исследование с учетом дискретности, необходимо провести z- преобразование.

Проводится z-преобразование, учитывая дискретность системы Т₀= 0,15с.

Для передаточной функции системы по таблице z – преобразований получим z – изображение передаточной функции, и предварительно умножив его на фиксатор нулевого порядка , получим следующее изображение передаточной функции замкнутой дискретной системы :

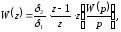(16)

где - отношение разрядностей ЦАП и АЦП

– экстраполятор нулевого порядка.

Используя программу MatLab, по полученной общей передаточной функции произведем z-преобразование.

Текст рабочей программы имеет вид:

Создадим tf объект:

W=tf([20400 1.2],[51 3136 8000 396000])

Transfer function:

20400 s + 1.2

-----------------------------------

51 s^3 + 3136 s^2 + 8000 s + 396000

Wd = c2d(W, 0.15)

Transfer function:

0.454 z^2 - 0.3554 z - 0.09856

--------------------------------------

z^3 - 0.8388 z^2 + 0.9545 z - 0.002136

Sampling time: 0.15

step(Wd)

Рисунок 9 -График переходного процесса после z-преобразования

Для проверки устойчивости системы после перехода от линейной к дискретной форме применяется критерий Шур-Кона. Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме Z - преобразования.Следовательно, передаточная функция дискретной системы:

Характеристическое уравнение дискретной функции имеет вид:

Коэффициенты характеристического уравнения:

Составим и вычислим определители Шур-Кона:

(17)

(18)

₍₁₉₎

Получили, что корни характеристического уравнения лежат внутри единичной окружности, так как коэффициенты уравнения удовлетворяют определителям Шур-Кона, имеющим значения: ∆К<0, для нечетных К и ∆К>0, для четных K. Следовательно, дискретная система устойчивая.

4 ПОСТРОЕНИЕ ЛАЧХ И ЛФЧХ СИСТЕМЫ И ЕЁ АНАЛИЗ

Лачх системы строится по передаточной функции разомкнутой системы, учитывая микропроцессор.

Рисунок 10- Структурная схема разомкнутой системы

Найдем передаточную функцию разомкнутой линейной системы:

(20)

Подставляя значения, передаточная функция разомкнутой линейной системы имеет вид:

Используя программу MATLAB получим z-преобразование:

W=tf([396000],[51 3136 8000])

Transfer function:

396000

----------------------

51 s^2 + 3136 s + 8000

Wd = c2d(W, 0.15)

Transfer function:

14.74 z + 1.573

---------------------------

z^2 - 0.6705 z + 9.869e-005

Далее необходимо перейти к псевдочастоте, осуществив биполярные реобразования. Для этого производится замена:

_. (21)

А затем перейдем от ω-изображению к передаточной функции от псевдочастоты, сделав подстановку:

, (22)

где Т₀=0,15 с - период дискретизации системы.

Следовательно, получим передаточную функцию дискретной разомкнутой системы:

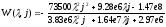(23)

Построим ЛАЧХ и ЛФЧХ по полученной передаточной функции псевдочастот в программе MatLab:

Q=tf([-73500 -9280000 147000000],[-3830000 -16400000 -2970000])

Transfer function:

73500 s^2 + 9.28e006 s- 1.47e008

--------------------------------------------------

3.83e006 s^2 + 1.64e007 s+ 2.97e006

margin(Q), grid

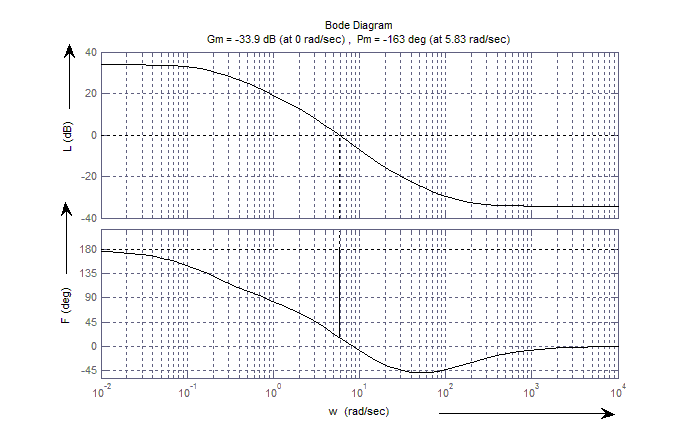
Рисунок 11 - ЛАЧХ и ЛФЧХ разомкнутой системы

5 ПОСТРОЕНИЕ ЖЛАЧХ И ЖЛФЧХ . ЛАЧХ КОРРЕТИРУЮЩЕГО УСТРОЙСТВА

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ (ЖЛАЧХ) состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной. Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики. Поскольку в исходной САУ присутствует дискретное устройство, построение желаемой ЛАЧХ ведется методом запретной зоны.Построим ЖЛАЧХ методом запретной зоны. Для построения ЖЛАЧХ необходимо найти запретную зону, ниже которой ЖЛАЧХ не может опускаться.

Исходными данными для построения служат параметры из технического задания. Перерегулирование системы составляет:

σ=40%,

Время регулирования системы:

t_p=10 с,

Колебательность принимает значение:

M= 29,7,

Период дискретизации системы:

Т₀=0,15 с .

Скорость изменения входной величины:

g' = А∙sin(ω∙t) =77 м/с, (24)

Ускорение изменения входной величины:

g'' =A∙cos(ω∙t) = 534 м/с², (25)

Частоты рабочей точки определяется по формуле:

с^-1. (26)

Вычисляем амплитуду рабочей точки:

. (27)

Получили точку А = (;).

Через полученную точку проводим прямую с наклоном –20 дБ/дек таким образом, чтобы она пересекала обе оси. Все, что лежит ниже получившейся прямой будет запретной зоной.

По номограмме Солодовникова определяем требуемое значение вещественной частотной функции Р_max, а по этому значению и кривой t_р находим время регулирования:

Рисунок 12 - Номограмма Солодовникова

Так как σ=40%, то по номограмме Солодовникова определяемР_max(ω)=1,35, а время регулирования определяется по формуле:

, (28)

По графику определяем, что время регулирования равно:

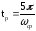. (29)

Время регулирования системы t_p=10 с. Находим частоту среза:

(30)

Найденное значение ω_ср наносим на шкалу частот.

Через полученную точку проводим асимптоту желаемой ЛАЧХ с наклоном –20 дБ/дек. Проведем две параллельные прямые, которые будут ограничивать асимптоту с наклоном –20 дБ/дек.

Показатель колебательности M характеризует склонность системы к колебаниям. Чем больше М, тем меньше запас устойчивости системы. найдем среднечастотную область построения ЖЛАЧХ.

(31)

Найдем границы среднечастотной области. Верхней границе этой области соответствует значение:

(32)

Нижней:

(33)

Передаточная функция желаемой ЛАЧХ будет иметь вид:

(34)

где ;

;

k=60.

Подставляя значения в функцию получим:

. (35)

Рисунок 13 – Желаемая ЛАЧХ

Построить ЛАЧХ корректирующего устройства можно с помощью графического вычитания желаемой ЛАЧХ из реальной ЛАЧХ:

(36)

По выражению строим ЛАЧХ корректирующего устройства рисунок 14, из графика видно, что передаточная функция корректирующего устройства имеет вид:

(37)

Рисунок 14- ЛАЧХ корректирующего устройства

6 РАСЧЕТ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

6.1 Расчет аналогового корректирующего устройства

Для коррекции в системе применяется корректирующее устройство (КУ) последовательного типа, так как необходимо улучшить динамические характеристики системы, косвенно влияя на величину их ошибки, также необходимо понизить частоту среза. КУ можно включать между различными элементами исходной системы. При выборе места включения руководствуются значением вносимой устройством погрешности. Наиболее предпочтительным вариантом является установка корректирующего устройства в электрическую цепь после микропроцессора, так как именно под влиянием этого элемента данная система изменила некоторые свои характеристики на менее предпочтительные.

По таблицам из атласа Топчеева, подберем корректирующее устройство по полученной ЛАЧХ (рисунок 15).