Типовая электрическая схема вч лампового генератора

Типовая электрическая схема ВЧ генератора, приведенная на рис. 6.1, содержит: электровакуумный прибор — тетрод; выходную электрическую цепь параллельный колебательный контур; вход­ную электрическую цепь - высокочастотный трансформатор; цепи питания анода, управляющей и экранной сеток.

Амплитудно-частотная характеристика параллельного колеба­тельного контура, включенного в анодной цепи, определяется вы­ражением

(6.1)

где Upeз — напряжение при резонансной частоте ƒpeз; Q — доброт­ность контура; х = (ƒ - ƒрез)/ƒрез - относительное отклонение часто­ты сигнала от резонансной частоты

(6-2)

где Lк, Ск — индуктивность и емкость контура (см. рис. 6.1).

Графики функции (6.1) при Q = 30 и Q = 100 приведены на рис. 6.2. Из них следует, что помимо согласования с нагрузкой параллельный колебательный контур выполняет и функцию филь­тра, так как при Q » 1 даже при небольшом отклонении частоты усиливаемого сигнала ƒ от резонансной частоты ƒрез напряжение на нем резко падает. Из (6.1) следует, что при Q » 1 полоса пропус­кания контура, измеренная по уровню 0,707 от максимума:

(6 3)

Благодаря узкой полосе пропускания анодного контура при его настройке в резонанс с частотой входного сигнала (ƒ =ƒрез) напря­жение на выходе генератора является синусоидальным, т.е. таким, как показано на рис. 5.2.

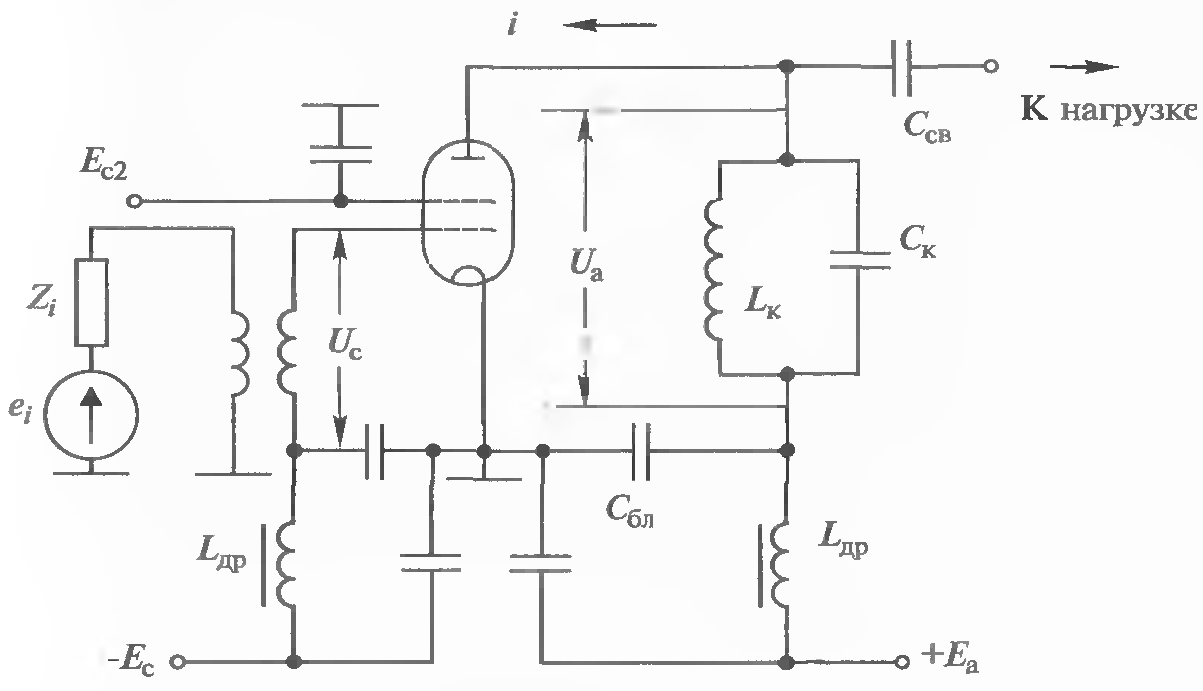рис 6.1

Напряжение на входе лампы, подводимое между управляющей сеткой и катодом (при заземленном катоде), складывается из высокочастотного сигнала источника возбуждения ис и постоянного напряжения смещения Ес:

(6.4)

где Ucm — амплитуда ВЧ сигнала.

Напряжение на выходе лампы, снимаемое с электродов анод-катод, складывается из постоянного напряжения Еа и высокочас­тотного напряжения uа на анодном контуре, резонансная частота которого ƒрез = ƒ - частоте входного сигнала Поскольку лампа по­ворачивает фазу сигнала на 180°, то перед uа следует поставить так «-».

В результате запишем

(6.5)

где Uam — амплитуда ВЧ сигнала на анодном контуре.

Для связи с нагрузкой в схеме (см. рис. 6.1) служит емкость Ссв, не пропускающая на выход ВЧ генератора постоянное напряжение. Для защиты от проникновения ВЧ сигнала в цепи питания последовательно с источниками постоянного напряжения включены дроссели Lдр. Той же цели служат и относительно большой емкости блокировочные конденсаторы Сбл, включенные во все цепи питания, замыкающие ВЧ сигнала на землю.

Определение токов и напряжений в ламповом вч генераторе

Определим анодный и сеточный токи в электровакуумном при­боре графическим путем при аппроксимированных анодно-сеточной и сеточной характеристиках (см. рис. 6.4, а) и входном ВЧ сигнале (6.4). Необходимые построения по определению данных токов показаны на рис. 6.5.

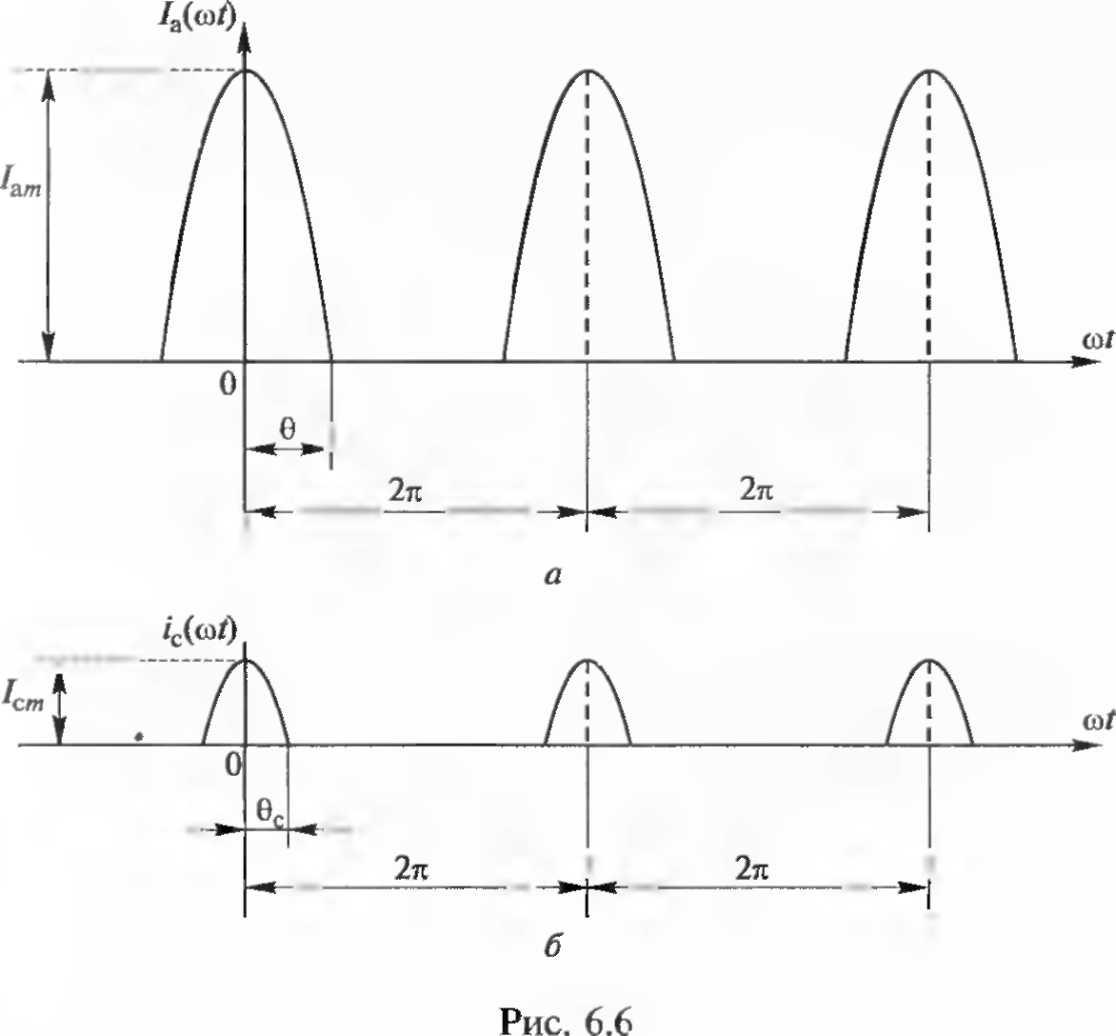
При выполнении построений принято во внимание, что анод­ный ток iа(t) протекает только при мгновенном значении напря­жения на управляющей сетке ec(t) > Е'с, а сеточный iс(t) - при ec(t) > 0. При остальных значениях напряжения ec(t) эти токи равны нулю. В результате анодный и сеточный токи приобретают форму импульсов косинусоидальной формы (часть синусоидаль­ного входного сигнала как бы «отсекается»). Эти импульсы ха­рактеризуются амплитудой и длительностью или фазой у основа­ния, половина которой называется углом отсечки. Импульсы анод­ного тока имеют амплитуду Iаm и угол отсечки Ɵ, импульсы сеточ­ного тока — Iаm, Ɵс. Такие импульсы периодически повторяются через ωt = 2π. Таким образом, в анодной цепи лампы протекает ток ia(t) импульсной формы (рис. 6.6, а), а в сеточной — ток iс(t) (рис. 6.6, б).

Проведем ось ординат посредине первого косинусоидального импульса. Тогда согласно рис. 6.5 и 6.6, а для анодного тока при запишем:

(6.9)

где S— крутизна анодно-сеточной характеристики (см. рис. 6.4, а); Ucm — амплитуда входного ВЧ сигнала (см. рис. 6.5).

Из (6.9) при ωt = 0 получим для амплитуды анодного тока

(6.10)

Косинус угла отсечки анодного тока согласно рис. 6.5

(6.11)

Аналогичным образом для сеточного тока согласно рис. 6.5 и ь, 6 при запишем:

Из (6.12) при ωt = 0 получим для амплитуды сеточного тока

(6.13)

Косинус угла отсечки сеточного тока согласно рис. 6.5

Разложим периодическую функцию i_a(t) в ряд Фурье. Поскольку функция согласно (6.9) и рис. 6.6 является симметричной относительно оси ординат, то ряд Фурье включает только постоянную и косинусные составляющие. В результате для анодного тока имеем

где — постоянная составляющая;

- n-я гармоника анодного тока, где n = 1, 2, 3 ...

Вычислив первый определенный интеграл, получим для постоянной составляющей анодного тока с учетом (6.10)

Вычислив второй определенный интеграл, получим для п-й гар­моники анодного тока с учетом (6.10)

Введем еще один параметр, называемый коэффициентом фор­мы косинусоидального импульса:

Зависимости называются коэффициентами разложения в ряд Фурье последовательности косинусоидальных импульсов (см. рис. 6.6, а). Составив программу, можно с помощью компьютера с требуемым шагом рассчитать все коэффициенты в зависимости от значения угла отсечки 0. Такая таблица с программой на языке Mathcad при­ведена в Приложении, а графики функций даны на рис. 6.7.

Разложение в ряд Фурье периодической последовательности импульсов сеточного тока (см. рис. 6.6, б) производится по той же методике, что и импульсов анодного тока:

Постоянная составляющая сеточного тока Iс0 определяется по формуле, аналогичной (6.16), в которой амплитуду Iam следует заменить на Iсm (6.13), а угол отсечки Ɵ на Ɵс (6.14). Гармоники сеточного тока определяются по формуле (6.17), в которой следует произвести аналогичные замены. В результате получим:

Определим напряжение на анодном контуре uа(t) (см. рис. 6.1) Как было показано в подразд. 6.1, при добротности контура Q » 1 он имеет узкую полосу пропускания (см. рис. 6.2) и обладает филь­трующими свойствами. Поэтому при настройке контура в резо­нанс с частотой входного сигнала (ƒ = ƒрез) он имеет большое сопротивление на частоте 1-й гармоники:

где - волновое сопротивление контура и малое, близкое к нулю, ма всех остальных гармониках - 2, 3-й и т.д.

Такое свойство контура позволяет считать напряжение на нем синусоидальным

(6.23)

(6.24)

амплитуда напряжения 1-й гармоники на контуре.