
- •Динамика твердого тела краткая теория
- •Определение момента инерции
- •Момент инерции сплошного цилиндра
- •Теорема Штейнера
- •Кинетическая энергия вращающегося твердого тела
- •Плоское движение твердого тела
- •Момент силы. Уравнение динамики вращательного движения твердого тела Момент силы
- •Уравнение динамики вращательного движения твердого тела
- •Момент импульса
- •Закон сохранения момента импульса
- •Некоторые демонстрации закона сохранения момента импульса
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Приложение Формулы алгебры и тригонометрии
- •Некоторые сведения о векторах
- •Рекомендуемая литература
Задачи для самостоятельного решения
1 Имеется тело
произвольной формы. Выберем точку
 на
некоторой оси
на
некоторой оси
 .
Мысленно
разобьем тело на элементарные
объемы с массами
.
Мысленно
разобьем тело на элементарные
объемы с массами
 и
проведем векторы
и
проведем векторы
 из
точки
из
точки в точки, где находятся элементарные
массы (рисунок 12). По какой из приведенных
формул можно вычислить момент инерции
тела относительно оси
в точки, где находятся элементарные
массы (рисунок 12). По какой из приведенных
формул можно вычислить момент инерции
тела относительно оси
 :
а)
:
а)
 ;
б)
;
б)
 ;
в)
;
в)
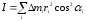 ?
?
Рисунок 12 – Рисунок к задаче 1
2 Найти
моменты инерции однородного диска массы
 и радиуса
и радиуса
 относительно осей, проходящих через
точки
относительно осей, проходящих через
точки
 и
и
 перпендикулярно его плоскости (рисунок
13).
перпендикулярно его плоскости (рисунок
13).

Рисунок 13 – Рисунок к задаче 2
3 Найти
момент инерции диска массы
 и радиуса
и радиуса
 относительно
оси, лежащей в плоскости диска и
совпадающей с его диаметром.
относительно
оси, лежащей в плоскости диска и
совпадающей с его диаметром.
4 Пустотелый
цилиндр с очень тонкими стенками имеет
массу
 и радиус
и радиус
 .
Найти
его моменты инерции относительно
осей
.
Найти
его моменты инерции относительно
осей
 и
и
 (рисунок
14).
(рисунок
14).

Рисунок 14 – Рисунок к задаче 4
5 Моменты
инерции тела относительно трех осей,
проходящих
через точки
 и перпендикулярных плоскости рисунка,
равны между собой. Точки
и перпендикулярных плоскости рисунка,
равны между собой. Точки
 и
и
 не лежат на одной прямой (рисунок 15).
Найти геометрическим
построением положение оси, проходящей
через центр масс
и параллельной указанным осям.
не лежат на одной прямой (рисунок 15).
Найти геометрическим
построением положение оси, проходящей
через центр масс
и параллельной указанным осям.
Рисунок 15 –
Рисунок к задаче 5
6 Две частицы (материальные точки) с массами m1 и m2 соединены жестким невесомым стержнем длины l. Найти момент инерции I этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.
Ответ: I=μl2, где μ=m1m2/(m1+m2) – приведенная масса частиц.
7
Найти: а) моменты инерции прямоугольной
пластинки относительно
оси
 (рисунок
16); б)
тонкой
однородной прямоугольной пластинки
относительно
оси z
(рисунок
16), проходящей через одну из вершин
пластинки перпендикулярно к ее плоскости,
если стороны пластинки равны
(рисунок
16); б)
тонкой
однородной прямоугольной пластинки
относительно
оси z
(рисунок
16), проходящей через одну из вершин
пластинки перпендикулярно к ее плоскости,
если стороны пластинки равны
 и
и
 ,
а ее масса -
,
а ее масса -
 .
Известны масса пластинки
.
Известны масса пластинки
 ,
ее размеры
,
ее размеры
 и
и
 .
.
Рисунок 16 –
Рисунок к задаче 7
8 Найти
момент инерции
 шарового
слоя малой толщины
шарового
слоя малой толщины
 ,
где
,
где
 -
средний радиус слоя. Масса шарового
слоя равна
-
средний радиус слоя. Масса шарового
слоя равна
 .
.
9
Найти момент инерции
тонкого
однородного стержня относительно оси,
перпендикулярной
к стержню и проходящей через его конец,
если масса стержня
 и его длина
и его длина
 .
.
Ответ:
 .
.




10 Найти момент
инерции тонкого проволочного кольца
радиусом R
и массы т
относительно оси,
совпадающей с его диаметром.
Ответ:
 .
.
11 Тонкая однородная
пластинка массы
 имеет форму равнобедренного прямоугольного
треугольника. Найти ее момент инерции
относительно оси, совпадающей с одним
из катетов, длина которого
имеет форму равнобедренного прямоугольного
треугольника. Найти ее момент инерции
относительно оси, совпадающей с одним
из катетов, длина которого
 .
.
Ответ:
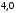 г·м2.
г·м2.
12 Вычислить момент
инерции: а)
медного
однородного диска относительно оси
симметрии,
перпендикулярной к плоскости диска,
если его толщина
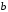 и радиус
и радиус
 ;
б)
однородного сплошного конуса относительно
его оси симметрии, если масса конуса т
и радиус его
основания
;
б)
однородного сплошного конуса относительно
его оси симметрии, если масса конуса т
и радиус его
основания
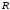 .
.
Ответ: а)
 ;
б)
;
б)
 .
.
13 Однородный диск
радиуса R
имеет круглый
вырез (рисунок 17). Масса оставшейся
(заштрихованной) части
диска равна т.
Найти
момент инерции такого диска относительно
оси, перпендикулярной к плоскости диска
и проходящей:
а)
через точку
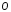 ;
б)
через его центр масс.
;
б)
через его центр масс.
Ответ: а)
 ;
б)
;
б)
 .
.

Рисунок 17 – Рисунок к задаче 13
14 Исходя из формулы для момента инерции однородного шара, найти момент инерции тонкого сферического слоя массы т и радиуса R относительно оси, проходящей через его центр.
Ответ:
 .
.
15 Определить
момент инерции полого шара массы m
относительно оси, проходящей через
центр тяжести. Внешний радиус шара
 ,
внутренний -
,
внутренний -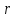 .
.
16 Найти момент инерции I однородного круглого прямого цилиндра массы т и радиуса R относительно оси цилиндра.
Ответ: I=½mR2.
17 Найти момент инерции I однородного куба относительно оси, проходящей через центры противолежащих граней. Масса куба m, длина ребра а.
Ответ: I=1/6ma2.
18 Найти момент инерции однородной пирамиды, основанием которой служит квадрат со стороной а, относительно оси, проходящей через вершину и центр основания. Масса пирамида равна m.
Ответ: I=1/10ma2.
19 Поверхностная
плотность тонкого диска радиуса
 изменяется по закону
изменяется по закону
 .
Найти момент инерции
.
Найти момент инерции
 диска относительно оси, проходящей
через центр диска
перпендикулярно егo
плоскости.
диска относительно оси, проходящей
через центр диска
перпендикулярно егo
плоскости.
Ответ:
 .
.
20 К точке с
радиус-вектором
 приложена
сила
приложена
сила
 ,
а к точке с
,
а к точке с
 - сила
- сила
 .
Здесь оба
радиус-вектора определены относительно
начала координат
.
Здесь оба
радиус-вектора определены относительно
начала координат
 ,
,
 и
и
 - орты осей х
и
у,
А и
В
- постоянные.
Найти плечо
равнодействующей силы относительно
точки
- орты осей х
и
у,
А и
В
- постоянные.
Найти плечо
равнодействующей силы относительно
точки
 .
.
Ответ:
 .
.
21 Снаряд массы m начинает движение со скоростью v0, направленной пол углом α к горизонту. Найти зависимость момента силы тяжести снаряда относительно точки выстрела от времени. Определить эту величину для моментов нахождения снаряда в высшей и наиболее удаленной точке траектории.
Ответ:
 ;
;
 ;
;
 .
.
22 Сила
с компонентами (3,4,5)(Н)
приложена к точке с координатами
(4,2,3,)(м).
Найти:
а) момент силы
 относительно начала координат;
б) модуль вектора
относительно начала координат;
б) модуль вектора
 ,
в) момент
силы
,
в) момент
силы
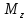 относительно оси z.
относительно оси z.
Ответ:
а)
 (Н·м);
б)
(Н·м);
б)
 Н·м;
в)
Н·м;
в)
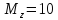 Н·м.
Н·м.
23 Сила,
приложенная к частице, имеет вид
 (Н).
Чему равен момент
этой
силы
(Н).
Чему равен момент
этой
силы
 относительно
оси z,
если точка приложения силы имеет
координаты
(4,2;
6,8; 0) (м).
относительно
оси z,
если точка приложения силы имеет
координаты
(4,2;
6,8; 0) (м).
Ответ:
 Н∙м.
Н∙м.
24 К
точке, радиус-вектор которой относительно
начала координат равен
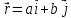 приложена
сила
приложена
сила
 .
Найти момент силы и плечо силы относительно
начала координат.
.
Найти момент силы и плечо силы относительно
начала координат.
Ответ:
 ,
,
 .
.
25 Частица, положение
которой относительно начала отсчёта
декартовой системы координат (точка О)
даётся радиус-вектором
 (-2,1,-5)(м),
имеет импульс
(-2,1,-5)(м),
имеет импульс
 (1,2,3)(кг·м/с).
Определить: а) момент импульса
(1,2,3)(кг·м/с).
Определить: а) момент импульса
 частицы относительно точки О;
б) моменты импульса Lx,
Ly
и
Lz
относительно осей x,y,z.
частицы относительно точки О;
б) моменты импульса Lx,
Ly
и
Lz
относительно осей x,y,z.
Ответ: а)
 (кг·м2/с);
б) Lx=13
кг·м2/с,
Ly=1
кг·м2/с,
Lz=-5
кг·м2/с.
(кг·м2/с);
б) Lx=13
кг·м2/с,
Ly=1
кг·м2/с,
Lz=-5
кг·м2/с.
26 Тело массы m
брошено из точки с координатами (0,2,0)(м)
вверх по вертикали с начальной скоростью
10м/с.
Найти приращение момента импульса Δ относительно начала координат за всё
время полёта тела. Ось z
направлена вверх. Сопротивлением воздуха
пренебречь.
относительно начала координат за всё
время полёта тела. Ось z
направлена вверх. Сопротивлением воздуха
пренебречь.
Ответ: Δ (-40,0,0)
(кг·м2/с).
(-40,0,0)
(кг·м2/с).
27 Тело массы m
брошено с начальной скоростью
 ,
образующей угол α
с горизонтом. Приняв плоскость, в которой
движется тело, за плоскость xy
и направив ось y
вверх, а ось
х
– по направлению движения, найти вектор
момента импульса тела относительно
точки бросания в момент, когда тело
находится в верхней точке траектории.
Сопротивлением воздуха пренебречь.
,
образующей угол α
с горизонтом. Приняв плоскость, в которой
движется тело, за плоскость xy
и направив ось y
вверх, а ось
х
– по направлению движения, найти вектор
момента импульса тела относительно
точки бросания в момент, когда тело
находится в верхней точке траектории.
Сопротивлением воздуха пренебречь.
Ответ:
 .
.
28
Момент
импульса частицы относительно некоторой
точки А
зависит от времени по закону
 .
Найти относительно точки А
момент силы
.
Найти относительно точки А
момент силы
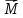 ,
действующий на
частицу.
Чему равен момент силы, когда угол между
,
действующий на
частицу.
Чему равен момент силы, когда угол между
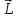 и
и
 равен
60°?
равен
60°?
29 Диск
насажен на неподвижную ось. К одной
и той
же точке
 диска
диска
прикладывают
одну из сил
 ,
, или
или
 .
Соотношение модулей сил указано на
рисунке 18. Под действием какой из сил
угловое ускорение будет наибольшим?
.
Соотношение модулей сил указано на
рисунке 18. Под действием какой из сил
угловое ускорение будет наибольшим?
30 Математический маятник массы m, длины l колеблется в вертикальной плоскости. Максимальное отклонение от положения равновесия равно l0 . Как изменяется момент силы тяжести маятника относительно точки подвеса в процессе движения? Нарисовать график зависимости момента силы тяжести маятника относительно точки подвеса от величины угла α.
Рисунок
18 –
Рисунок к задаче 29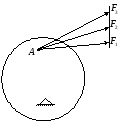
31 К
однородному стержню массы
 и
длины
и
длины
 приложены две силы
приложены две силы
 и
и
 (рисунок 19). Найти ускорение
точки
(рисунок 19). Найти ускорение
точки
 и угловое ускорение стержня. Как изменится
ответ, если
силу
и угловое ускорение стержня. Как изменится
ответ, если
силу
 приложить к точке
приложить к точке
 ?
?
Рисунок 19 – Рисунок к задаче 31
32 Тело произвольной формы вращается вокруг оси OO с угловой скоростью ω. Доказать, что угловая скорость вращения тела вокруг любой другой оси O'O' параллельной оси OO, также равна ω.
33 Обруч
массы
 и радиуса
и радиуса
 вращается с угловой скоростью
вращается с угловой скоростью
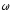 вокруг неподвижной оси
вокруг неподвижной оси
 ,
проходящей через центр
обруча (точка
,
проходящей через центр
обруча (точка
 )
перпендикулярно его плоскости. Найти
момент импульса обруча: а)
относительно точки
)
перпендикулярно его плоскости. Найти
момент импульса обруча: а)
относительно точки
 ;
б) относительно
точки
;
б) относительно
точки
 ,
лежащей на оси вращения.
,
лежащей на оси вращения.
34 Точка
1 тела, вручающегося с угловой скоростью
 ,
имеет в некоторый момент времени скорость
,
имеет в некоторый момент времени скорость
 .
Найти для того же момента времени
скорость
.
Найти для того же момента времени
скорость
 точки 2, смещенной
относительно точки 1 на
точки 2, смещенной
относительно точки 1 на
 .
.
Ответ:
 +
+ .
.
35 Однородный шар
массы
 движется поступательно
по поверхности стола под действием
постоянной
силы
движется поступательно
по поверхности стола под действием
постоянной
силы
 ,
приложенной, как показано на рисунке
20, где угол
,
приложенной, как показано на рисунке
20, где угол
 .
Коэффициент трения между шаром и столом
.
Коэффициент трения между шаром и столом
 .
Найти F
и ускорение
шара.
.
Найти F
и ускорение
шара.
Ответ: F=
 а=
а=
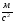 .
.

Рисунок 20 – Рисунок к задаче 35
36 На ступенчатый
блок (рисунок 21) намотаны в противоположных
направлениях две нити. На конец одной
нити действуют постоянной силой
 ,
а к концу другой нити прикреплен груз
массы т.
Известны
радиусы
,
а к концу другой нити прикреплен груз
массы т.
Известны
радиусы
 и
и
 блока
и его момент инерции
блока
и его момент инерции
 относительно оси вращения.
Трения нет. Найти угловое ускорение
блока.
относительно оси вращения.
Трения нет. Найти угловое ускорение
блока.
Ответ:
 ,
где ось z
направлена за плоскость рисунка 21.
,
где ось z
направлена за плоскость рисунка 21.
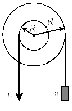
Рисунок 21 – Рисунок к задаче 36
37 На
однородный сплошной цилиндр массы
 и радиуса
R
плотно
намотана легкая нить, к концу которой
прикреплен груз массы т
(рисунок
22). В момент
и радиуса
R
плотно
намотана легкая нить, к концу которой
прикреплен груз массы т
(рисунок
22). В момент
 система пришла в движение. Пренебрегая
трением в оси цилиндра, найти зависимость
от времени: а)
модуля угловой скорости цилиндра; б)
кинетической
энергии всей системы.
система пришла в движение. Пренебрегая
трением в оси цилиндра, найти зависимость
от времени: а)
модуля угловой скорости цилиндра; б)
кинетической
энергии всей системы.
Ответ: а)
 ;
б)
;
б)
 .
.
Рисунок 22 – Рисунок к задаче 37
38 Горизонтальный
тонкий однородный стержень
 массы
т
и
длины
массы
т
и
длины
 может свободно вращаться вокруг
вертикальной
оси, проходящей через его конец
может свободно вращаться вокруг
вертикальной
оси, проходящей через его конец
 .
В некоторый
момент на конец
.
В некоторый
момент на конец
 начала
действовать постоянная сила
начала
действовать постоянная сила
 ,
которая все
время перпендикулярна к первоначальному
положению покоившегося стержня и
направлена в горизонтальной плоскости.
Найти угловую скорость стержня
как функцию его угла поворота
,
которая все
время перпендикулярна к первоначальному
положению покоившегося стержня и
направлена в горизонтальной плоскости.
Найти угловую скорость стержня
как функцию его угла поворота
 из начального положения.
из начального положения.
Ответ:
 .
.
39 В установке,
показанной на рисунке 23, известны масса
однородного сплошного цилиндра т,
его радиус
 и массы тел
и массы тел
 и
и
 .
Скольжения нити и трения в оси цилиндра
нет. Найти угловое ускорение
.
Скольжения нити и трения в оси цилиндра
нет. Найти угловое ускорение
 цилиндра и отношение натяжений
цилиндра и отношение натяжений
 вертикальных участков нити в процессе
движения. Убедиться, что при
вертикальных участков нити в процессе
движения. Убедиться, что при

 .
.
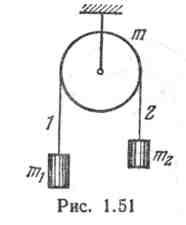
Рисунок 23 – Рисунок к задаче 39
Ответ:
 ,
,
 .
.
40 В системе,
показанной на рисунке 24, известны массы
тел
 и
и
 ,
коэффициент трения
,
коэффициент трения
 между телом
между телом
 и
горизонтальной плоскостью, а также
масса блока т,
который можно считать однородным диском.
Скольжения нити
по блоку нет. В момент
и
горизонтальной плоскостью, а также
масса блока т,
который можно считать однородным диском.
Скольжения нити
по блоку нет. В момент
 тело
тело
 начинает
опускаться.
Пренебрегая массой нити и трением в оси
блока, найти:
а)
ускорение тела
начинает
опускаться.
Пренебрегая массой нити и трением в оси
блока, найти:
а)
ускорение тела
 ;
б)
работу силы трения, действующей на тело
;
б)
работу силы трения, действующей на тело
 за первые t
секунд после
начала движения.
за первые t
секунд после
начала движения.

Рисунок 24 – Рисунок к задаче 40
Ответ: а)
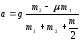 ;
б)
;
б)
 .
.
41 Однородный диск
радиуса R
раскрутили
до угловой
скорости
 и осторожно положили на горизонтальную
поверхность. Сколько времени диск будет
вращаться на поверхности, если коэффициент
трения равен
и осторожно положили на горизонтальную
поверхность. Сколько времени диск будет
вращаться на поверхности, если коэффициент
трения равен
 ?
?
Ответ:
 .
.
42 Маховик
с начальной угловой скоростью
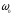 начинает
тормозиться силами, момент которых
относительно его оси пропорционален
квадратному корню из его
угловой скорости. Найти среднюю угловую
скорость маховика
за все время торможения.
начинает
тормозиться силами, момент которых
относительно его оси пропорционален
квадратному корню из его
угловой скорости. Найти среднюю угловую
скорость маховика
за все время торможения.
Ответ:
 .
.
43 Горизонтально
расположенный однородный стержень
 массы
массы
 и длины
и длины
 вращается свободно вокруг неподвижной
вертикальной оси
вращается свободно вокруг неподвижной
вертикальной оси
 ,
проходящей через его конец
,
проходящей через его конец
 .
Точка
.
Точка
 находится
посередине
оси
находится
посередине
оси
 ,
длина которой
,
длина которой
 .
При каком значении
угловой скорости стержня горизонтальная
составляющая
силы, действующей на нижний конец оси
.
При каком значении
угловой скорости стержня горизонтальная
составляющая
силы, действующей на нижний конец оси
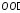 ,
будет
равна нулю? Какова при этом горизонтальная
составляющая
силы, действующей на верхний конец оси?
,
будет
равна нулю? Какова при этом горизонтальная
составляющая
силы, действующей на верхний конец оси?
Ответ:
 ;
;
 .
.
44 Однородный
цилиндр массы
 и радиуса
и радиуса
 (рисунок 26) в момент
(рисунок 26) в момент
 начинает опускаться под действием силы
тяжести. Пренебрегая массой нитей,
найти: а) угловое ускорение цилиндра;
б) зависимость от времени мгновенной
мощности, которую развивает сила тяжести.
начинает опускаться под действием силы
тяжести. Пренебрегая массой нитей,
найти: а) угловое ускорение цилиндра;
б) зависимость от времени мгновенной
мощности, которую развивает сила тяжести.










Ответ: а)
 ;
б)
;
б)
 .
.
45 Тонкие
нити намотаны на концах однородного
сплошного
цилиндра массы т.
Свободные
концы нитей прикреплены
к потолку кабины лифта. Кабина начала
подниматься
с ускорением
 .
Найти ускорение
.
Найти ускорение
 цилиндра
относительно кабины и силу
цилиндра
относительно кабины и силу
 ,
с которой цилиндр действует
(через нити) на потолок.
,
с которой цилиндр действует
(через нити) на потолок.
Ответ:
 ,
,
 .
.
46 На
гладкой наклонной плоскости, составляющей
угол
 с горизонтом, находится катушка с ниткой,
свободный
конец которой укреплен, как показано
на рисунке 26. Масса катушки
с горизонтом, находится катушка с ниткой,
свободный
конец которой укреплен, как показано
на рисунке 26. Масса катушки
 ,
ее момент инерции относительно
собственной оси
,
ее момент инерции относительно
собственной оси
 ,
радиус намотанного
слоя ниток
,
радиус намотанного
слоя ниток
 .
Найти ускорение оси катушки.
.
Найти ускорение оси катушки.
Ответ: а=
 .
.
Рисунок
26 –
Рисунок к задаче 46
47 Однородный
сплошной цилиндр массы т
лежит
на двух
горизонтальных брусьях. На цилиндр
намотана нить,
за свешивающийся конец которой тянут
с постоянной вертикально
направленной силой
 (рисунок
27). Найти значения силы
(рисунок
27). Найти значения силы
 ,
при которых
цилиндр будет катиться без скольжения,
если коэффициент трения равен
,
при которых
цилиндр будет катиться без скольжения,
если коэффициент трения равен
 .
.

Рисунок 27 – Рисунок к задаче 47
Ответ:
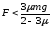 .
.
48 Система,
состоящая из цилиндрического катка
радиуса R
и гири, связанных нитью, перекинутой
через блок (рисунок 28) под действием
силы тяжести приходит в движение из
состояния
покоя. Определить ускорение центра масс
катка и силу натяжения нити. Какую
скорость приобретет гиря, если она
опускается с высоты h?
Масса цилиндра М,
масса
гири ,
массой блока пренебречь. Каток катится
без скольжения
,
массой блока пренебречь. Каток катится
без скольжения
Рисунок 28 –
Рисунок к задаче 48
49 На горизонтальной
шероховатой плоскости лежит катушка
ниток массы т.
Ее момент инерции относительно собственной
оси
 ,
где
,
где
 - числовой коэффициент,
- числовой коэффициент,
 - внешний радиус катушки. Радиус
намотанного
слоя ниток равен
- внешний радиус катушки. Радиус
намотанного
слоя ниток равен
 .
Катушку без скольжения начали тянуть
за нить постоянной силой
.
Катушку без скольжения начали тянуть
за нить постоянной силой
 ,
направленной под углом
,
направленной под углом
 к
горизонту
(рисунок 29). Найти: а)
проекцию на ось
к
горизонту
(рисунок 29). Найти: а)
проекцию на ось
 ускорения
оси катушки; б) работу силы
ускорения
оси катушки; б) работу силы
 за первые
за первые
 секунд движения.
секунд движения.

Рисунок 29 – Рисунок к задаче 49
Ответ: а)
 ;
б)
;
б)
 .
.
50 Система
(рисунок 30) состоит из двух одинаковых
однородных
цилиндров, на которые симметрично
намотаны
две легкие нити. Найти ускорение оси
нижнего цилиндра
в процессе движения. Трения в оси верхнего
цилиндра нет. Ответ:
 .
.

Рисунок 30 – Рисунок к задаче 50
51 В системе,
показанной на рисунке 31, известны масса
т груза
 ,
масса
,
масса
 ступенчатого
блока
ступенчатого
блока
 ,
момент
инерции
,
момент
инерции
 последнего относительно его оси и
последнего относительно его оси и
радиусы ступеней
блока R
и 2R.
Масса нитей пренебрежимо мала. Найти
ускорение груза
 .
.
Рисунок 31 – Рисунок к задаче 51
Ответ:
 .
.
52 Сплошной
однородный цилиндр
 массы
массы
 может
свободно вращаться вокруг горизонтальной
оси, которая укреплена на подставке
может
свободно вращаться вокруг горизонтальной
оси, которая укреплена на подставке
 массы
массы
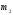 (рисунок 32). На цилиндр плотно намотана
легкая нить, к концу
(рисунок 32). На цилиндр плотно намотана
легкая нить, к концу
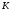 которой
приложили постоянную горизонтальную
силу
которой
приложили постоянную горизонтальную
силу
 .
Трения
между подставкой и опорной горизонтальной
плоскостью
нет.
Найти: а)
ускорение точки
.
Трения
между подставкой и опорной горизонтальной
плоскостью
нет.
Найти: а)
ускорение точки
 ;
б)
кинетическую
энергию этой системы через
;
б)
кинетическую
энергию этой системы через
 секунд
после
начала движения.
секунд
после
начала движения.

Рисунок 32 – Рисунок к задаче 52
Ответ: а)
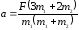 ;
б)
;
б)
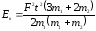 .
.
53 На гладкой
горизонтальной плоскости лежит доска
массы
 и на ней
однородный шар массы
и на ней
однородный шар массы
 .
К доске
приложили постоянную горизонтальную
силу
.
К доске
приложили постоянную горизонтальную
силу
 .
С какими
ускорениями будут двигаться доска и
центр шара в отсутствие скольжения
между ними?
.
С какими
ускорениями будут двигаться доска и
центр шара в отсутствие скольжения
между ними?
Ответ:
 ;
;
 .
.
54 Сплошному
однородному цилиндру массы т
и
радиуса R
сообщили
вращение вокруг его оси с угловой
скоростью
 ,
затем его положили боковой поверхностью
на
горизонтальную плоскость и предоставили
самому себе.
Коэффициент трения между цилиндром и
плоскостью равен
,
затем его положили боковой поверхностью
на
горизонтальную плоскость и предоставили
самому себе.
Коэффициент трения между цилиндром и
плоскостью равен
 .
Найти: а)
время,
в течение которого движение цилиндра
будет происходить
со скольжением; б)
полную работу силы трения скольжения.
.
Найти: а)
время,
в течение которого движение цилиндра
будет происходить
со скольжением; б)
полную работу силы трения скольжения.
Ответ: а)
 ;
б)
;
б)
 .
.
55 Однородный шар
радиуса
 скатывается
без скольжения
с вершины сферы радиуса
скатывается
без скольжения
с вершины сферы радиуса
 .
Найти угловую скорость
шара после отрыва от сферы. Начальная
.
Найти угловую скорость
шара после отрыва от сферы. Начальная
скорость шара пренебрежимо мала.
Ответ:
 .
.
56 Сплошной однородный
цилиндр радиуса R
катится по
горизонтальной плоскости, которая
переходит в наклонную плоскость,
составляющую угол
 с горизонтом
(под уклон). Найти максимальное значение
скорости
с горизонтом
(под уклон). Найти максимальное значение
скорости
 цилиндра,
при котором он перейдет на наклонную
плоскость еще без скачка. Считать, что
скольжения нет.
цилиндра,
при котором он перейдет на наклонную
плоскость еще без скачка. Считать, что
скольжения нет.
Ответ:
 .
.
57 Однородный шар
массы
 и радиуса
и радиуса
 катится без скольжения по горизонтальной
поверхности. Вследствие деформаций в
месте соприкосновения шара и плоскости
на шар при движении вправо действует
равнодействующая
катится без скольжения по горизонтальной
поверхности. Вследствие деформаций в
месте соприкосновения шара и плоскости
на шар при движении вправо действует
равнодействующая
 сил реакции, как показано на
рисунке 33. Найти модуль момента силы
сил реакции, как показано на
рисунке 33. Найти модуль момента силы
 относительно центра
относительно центра
 шара,
если шар, имевший в некоторый момент
скорость
шара,
если шар, имевший в некоторый момент
скорость
 ,
прошел после этого до остановки путь
,
прошел после этого до остановки путь
 .
Момент силы
.
Момент силы
 считать постоянным.
считать постоянным.

Рисунок 33 – Рисунок к задаче 57
Ответ:
 мН·м.
мН·м.
58 Однородный шар
скатывается без скольжения по наклонной
плоскости, составляющей угол
 с горизонтом. Найти ускорение центра
шара и значение коэффициента трения,
при котором скольжения не будет.
с горизонтом. Найти ускорение центра
шара и значение коэффициента трения,
при котором скольжения не будет.
Ответ:
 .
.
59 Однородный шар
массы
 скатывается без скольжения по наклонной
плоскости, составляющей угол
скатывается без скольжения по наклонной
плоскости, составляющей угол
 с горизонтом. Найти кинетическую энергию
шара через время
с горизонтом. Найти кинетическую энергию
шара через время
 после
начала движения.
после
начала движения.
Ответ:
 .
.
60 Какой
путь пройдет катящийся без скольжения
диск,
поднимаясь вверх по наклонной плоскости
с углом наклона
 ,
если ему сообщена начальная скорость
,
если ему сообщена начальная скорость
 ,
параллельная
наклонной плоскости.
,
параллельная
наклонной плоскости.
61 Горизонтальная платформа массой 25кг и радиусом 0,8м вращается с частотой 18мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определите частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5кг∙м2 до 1кг∙м2.
Ответ: 23 мин -1.
62 Человек массой 60кг, стоящий на краю горизонтальной платформы массой 120кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10мин-1, переходит к ее центру (рисунок 34). Считая платформу круглым однородным диском, а человека — точечной массой, определите, с какой частотой будет тогда вращаться платформа.
Ответ:
 .
.
Рисунок
34 –
Рисунок к задаче 62
