Контрольная работа №1 Вариант 1

1. Найти расстояние между центрами окружностей

.

2. Составить уравнение эллипса, фокусы которого расположены на оси ОХ, симметрично относительно начала координат, если – точки эллипса.

3. Уравнение линии привести к каноническому виду, построить ее.

4. Вычислить расстояние между прямыми и

5. Выяснить принадлежат ли точки , одной плоскости.

6. Докажите, что прямая лежит в плоскости

7. Даны вершины треугольника Вычислить длину его высоты, проведенной из вершины В на сторону АС.

8. Найти матрицу , где .

9. Решить систему матричным методом:

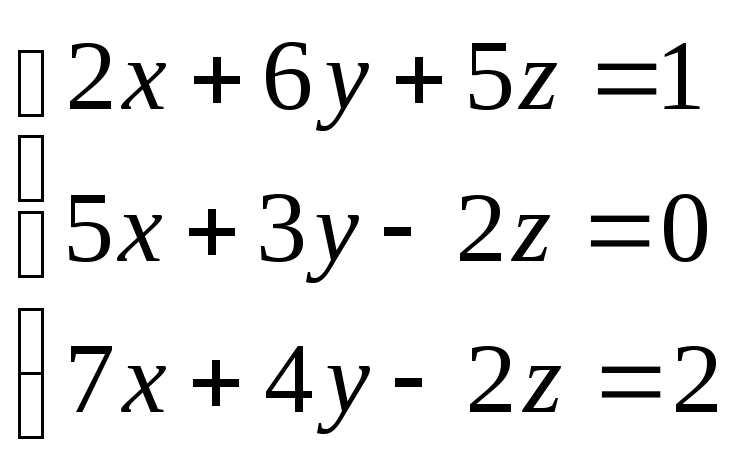
10. Используя теорему Кронекера–Капели, исследовать систему уравнений и в случае совместности решить ее:

11. Решить матричное уравнение: , где

12. Решить систему уравнений методом Гаусса:

13. Вычислить, какую работу производит сила , когда ее точка приложения перемещается из начала в конец вектора .

14. Найти орт вектора .

15. На плоскости даны два вектора и . Найти разложение вектора по базису

Контрольная работа №1 Вариант 2

1. Найти уравнение прямой, проходящей через центры окружностей .

2. Составить уравнение эллипса, фокусы которого расположены на оси ОХ, симметрично относительно начала координат, если точка принадлежит эллипсу,

3. Уравнение линии привести к каноническому виду, построить ее.

4. Найти уравнение прямой, проходящей через точку , и точку пересечения прямой с осью ОУ.

5. Найти угол между прямой и плоскостью

6. Найдите точку пересечения прямой и плоскости

7. Вычислить площадь треугольника с вершинами в точках

8. Найти матрицу , где .

9. Решить систему матричным методом:

10. Используя теорему Кронекера–Капели, исследовать систему уравнений и в случае совместности решить ее:

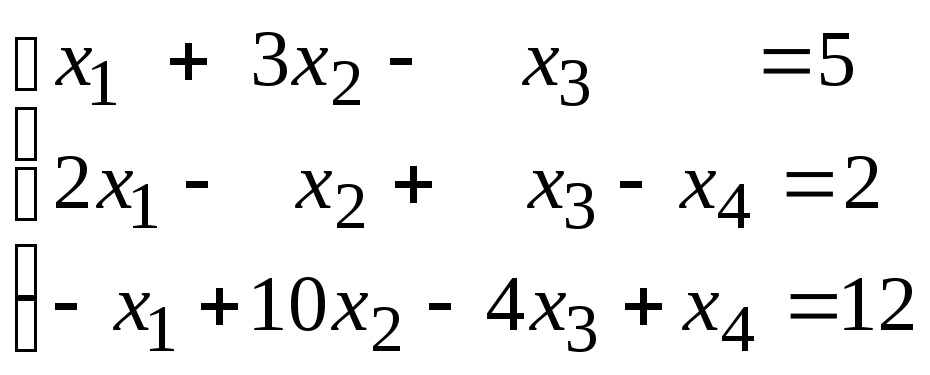
11. Решить матричные уравнения: , где

12. Решить систему уравнений методом Гаусса:

.

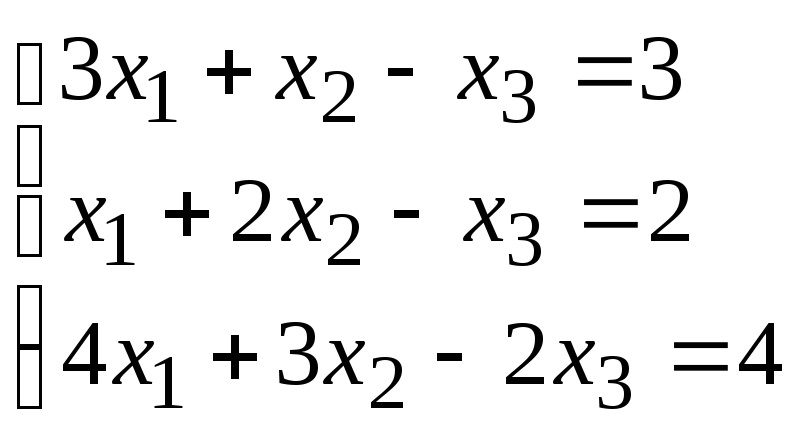13. Вычислить синус угла, образованного векторами и .

14. Найти орт вектора .

15. На плоскости даны два вектора и . Найти разложение вектора по базису

Контрольная работа №1 Вариант 3

1. Найти координаты центра и радиус окружности:

.

2. Составить уравнение эллипса, фокусы которого расположены на оси ОХ, симметрично относительно начала координат, если

3. Уравнение линии привести к каноническому виду, построить ее.

4. Написать уравнение прямой, проходящей через точку перпендикулярно прямой

5. Записать каноническое уравнение прямой:

6. Найдите точку пересечения прямой и плоскости

7. Дан треугольник с вершинами в точках . Написать уравнение медианы, проведенной из вершины А.

8. Найти матрицу , где

.

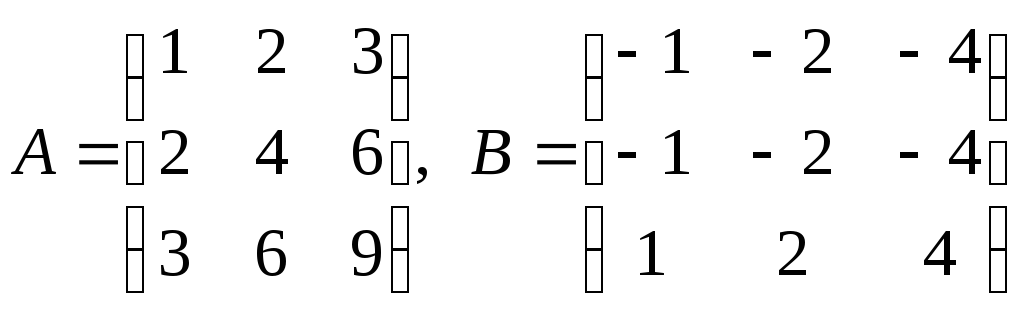9. Решить систему матричным методом:

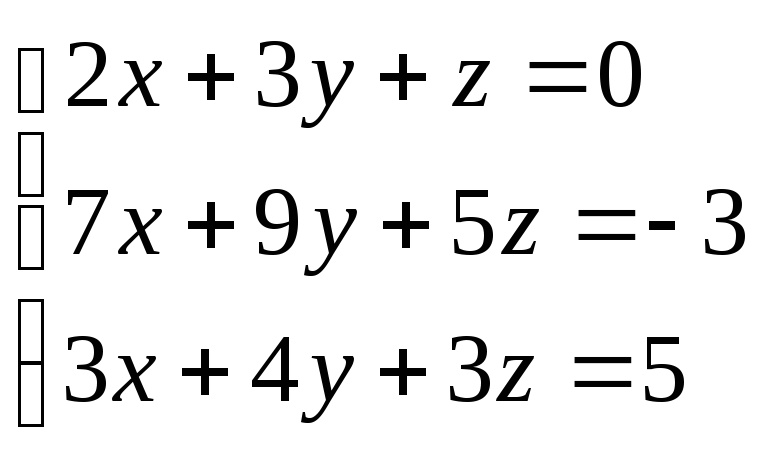
10. Используя теорему Кронекера–Капели, исследовать систему уравнений и в случае совместности решить ее:

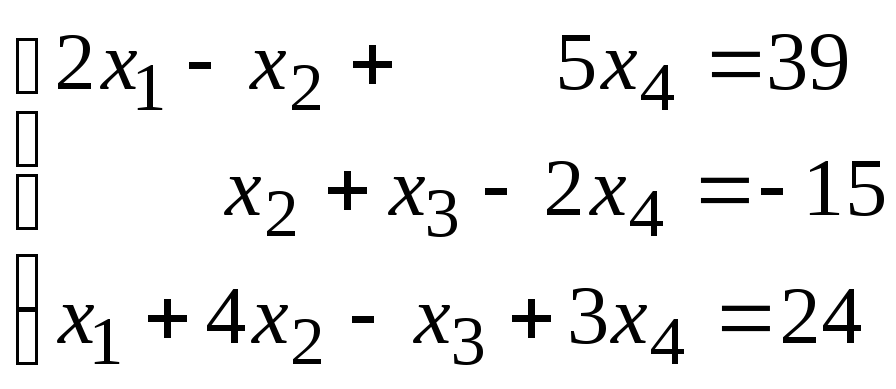
11. Решить матричное уравнение: , где

12. Решить систему уравнений методом Гаусса:

.

13. Даны и . Вычислить .

14. Найти орт вектора .

15. На плоскости даны два вектора и . Найти разложение вектора по базису