Примеры

Пример 2.1. Удельный вес бензина . Определить его плотность.

Решение:

Пример 2. 2. Плотность дизельного мазута . Определить его удельный вес.

Решение: ; .

Пример 2.3. При гидравлическом испытании трубопровода диа­метром d = 200 мм и длиной 250 м давление в трубе было повышено до 3 МПа. Через час давление снизилось до 2 МПа. Сколько воды вытекло через неплотности?

Решение:

1. Определим объем воды в трубопроводе:

м³.

2. Найдем изменение давления за время испытания:

МПа.

3. Принимая коэффициент объемного сжатия воды _Р = 510^-7 , находим количество воды, вытекающей через неплотности, по формуле

л.

3. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ И ДИНАМИКИ

Кинематика жидкости изучает связь между геометрическими характеристиками движения и времени (скоростью и ускорением).

Динамика жидкости изучает законы движения как результат действия сил.

3.1. Основные аналитические методы

исследования движения жидкости

3.1.1. Метод Лагранжа

Будем считать, что для каждой частицы нам известны зависимости

(3.1)

Пользуясь этими зависимостями, можно построить траектории намеченных частиц жидкости. Далее можно в любом месте этих траекторий найти длину пути ds, проходимого частицей за время dt. Например,

(3.2)

В данном случае мы следим за отдельными частицами жидкости в течение времени t, за которое эти частицы, двигаясь по своим траекториям, проходят всю рассматриваемую область.

Согласно Лагранжу, о потоке жидкости в целом можно судить по совокупному рассмотрению траекторий, описываемых частицами жидкости.

3.1.2. Метод Эйлера

Представим некоторую область, занятую движущейся жидкостью. Согласно Эйлеру, не следят за движением отдельных частиц жидкости и не интересуются их траекториями.

В соответствии с предложениями Эйлера намечают точки, которые считают скрепленными с рассматриваемым неподвижным пространством. Эти точки неподвижны при протекании через них жидкости. Здесь величины x, y, z не есть текущие координаты частиц жидкости, а просто координаты неподвижных точек пространства.

Рассмотрим момент времени . В этот момент времени в точке 1 будет находиться некоторая частица жидкости, имеющая скорость ; в этот же момент времени в точке 2 будем иметь скорость ; в точке 3 – скорость и т.д.

Согласно Эйлеру, поток в целом в данный момент времени оказывается представленным векторным полем скоростей, относящихся к неподвижным точкам пространства. В следующий момент времени получается другое поле скоростей. Сравнивая эти поля скоростей, можно судить о том, как поток ведет себя с течением времени.

Выше было отмечено, что координаты x, y, z, согласно Эйлеру, являются координатами неподвижных произвольных точек пространства. Поэтому в данном случае величины dx, dy, dz нельзя рассматривать как проекции элементарного пути, проходимого частицами жидкости за время dt. Эти величины здесь являются просто произвольными приращениями координат. В связи с этим зависимости (3.2) в случае метода Эйлера – неприемлемы.

Метод Лагранжа ввиду его сложности не нашел широкого применения в гидравлике. Далее в основном будет использоваться метод Эйлера, согласно которому следят за движением частиц в продолжение элементарного отрезка времени, когда данная частица жидкости проходит через рассматриваемую точку пространства.

Рассматривая индивидуальную производную как полную производную по времени от вектора скорости, представляющего сложную функцию от времени t как явно в случае нестационарного поля скоростей, так и через посредство координат x, y, z движущейся точки, найдем ускорение вектора скорости

, (3.3)

или, учитывая, что производные по времени от координат движущейся точки равны проекциям ее скорости на оси координат

получаем следующее выражение вектора ускорения в эйлеровых переменных:

(3.4)

Проекции рассматриваемого вектора ускорения на оси неподвижных координат вычисляются следующим образом:

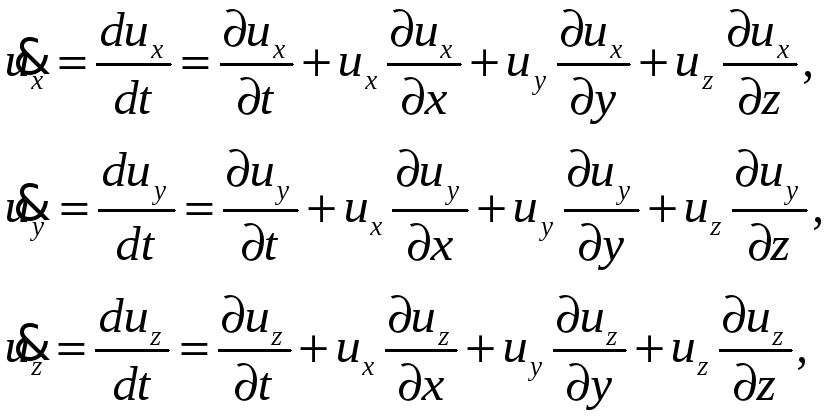(3.5)

где ; ; – индивидуальные или субстанциональные производные; ; ; – локальные производные, выражающие из­­менение во времени вектора u в фик­си­рованной точке пространства;

– конвективная производная вектора u. Эта величина выражает изменение ско­рос­ти в пространстве в данный момент вре­мени. При установившемся движении локальные ускорения равны нулю.