МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
___________________________________________
Казанский государственный
энергетический университет
Кафедра «Высшей математики»
ЭЛЕМЕНТЫ ТЕОРИИ
ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Базовые конспекты лекций
Казань 2006
УДК 517.31
ББК 22.161.1
Элементы теории операционного исчисления. Казань: Каз. гос. энерг. ун-т, 2006.
Работа включает краткие теоретические сведения по теме «Операционное исчисление». Вводится преобразование Лапласа, доказываются теоремы подобия, смещения, запаздывания. Вычисляются изображения основных элементарных функций. Рассматриваются простые приемы отыскания оригинала по изображению и основные правила дифференцирования и интегрирования оригиналов и изображений.
Работа предназначена для первичного знакомства студентов с базовыми понятиями и основными моментами теории операционного исчисления.
Данный учебный материал по составу и объему соответствует программам технических специальностей университета по высшей математике. Он представлен в четкой, сжатой форме, даны исходные определения и доказательства основных теорем. Это опорные конспекты лекций, на основе которых преподаватели кафедры «Высшая математика» КГЭУ организуют свои лекционные курсы по данной теме.
Авторский коллектив: Арсланов Ф.Х. , Гарифьянов Ф.Н. , Гимадиев Р.Ш. , Григорян С.А., Желифонов М.П., Липачева Е.В., Никитин А.С., Хамзин А.А.
© Казанский государственный энергетический университет, 2006
ЭЛЕМЕНТЫ ТЕОРИИ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Преобразование Лапласа
Пусть
функция f(t)
обладает
следующими свойствами: 10
f(t)
0
при t
< 0 ; 20
| f(t)|
< M
при t
> 0, где М
> 0 , т.е. f(t)
возрастает не быстрее некоторой
экспоненты и s0
– показатель
роста функции ;
30
На любом промежутке оси [a,b]
выполняются
условия Дирихле – функция кусочно-непрерывна
и имеет конечное число экстремумов и
точек разрыва I
рода.
Такие функции наз. изображаемыми по Лапласу или оригиналами. Запишем интеграл
=
F(p)
(
1 )
где
p
= s
+ iq
- комплексная переменная. При s
и F(p)
0 . При указанных условиях он сходится
и наз. интегралом
Лапласа, а
функция F(p)
наз. изображением
оригинала.
Переход от f(t)
к F(p)
наз. преобразованием
Лапласа и
обозначается f(t)
=: F(p)
или F(p)
=: f(t).
Для значения f(t)
в точке разрыва t0
выбирают f(t0)
= ½ [f(t0
- 0) + f(t0
+ 0)] . При
этих условиях между f(t)
и F(p)
существует взаимно – однозначное
соответствие.
Смысл преобразования – многим операциям над оригиналом соответствуют более простые операции над изображением. Например, решение дифференциальных и интегральных уравнений может существенно упроститься.
Нахождение изображений
Вычислим изображение единичной функции и экспоненты
Пр.1
(t)
=
,
(t)
=:
=
=
,
Re p > 0
Пр.2
=
,
=:
=
=
,
Re p > a = s0
Свойство линейности. Т.к. интеграл от суммы функций равен сумме интегра-лов, то линейной комбинации оригиналов соответствует линейная комбина-ция изображений.
С1 f1(t) + С2 f2(t) =: С1 F1(p) + С2 F2(p)
Из формулы Эйлера eit = cos t + i sin t имеем соs t = ½(eit + e-it) , sin t = ½i(eit - e-it) и для оригиналов этих функций вычислим изображения
Пр.3
f(t)
= cos t
= ½(eit
+ e-it)
=: ½ [
]
=
Пр.4
f(t)
= sin t
= ½i(eit
- e-it)
=: 1/2i
[
]
=
Пр.5
f(t)
= t
=:
=
=
+
=
=
.
f(t)
= t2
=:
=
=
+
+
=
=
.
Аналогично имеем t3
=:
,
t4
=:
,
. . . и получаем
tn
=:
.
Теоремы подобия, смещения, запаздывания
Теорема
подобия.
Дополнительное умножение аргумента
t
в оригинале на число а
R,
a
> 0 приводит в изображении к уменьшению
в а
раз параметра p
и самого изображения,
f(аt)
=:
F(
)
.
( 2 )
Доказательство.
f(аt)
=:
=
=
=
=
=
=
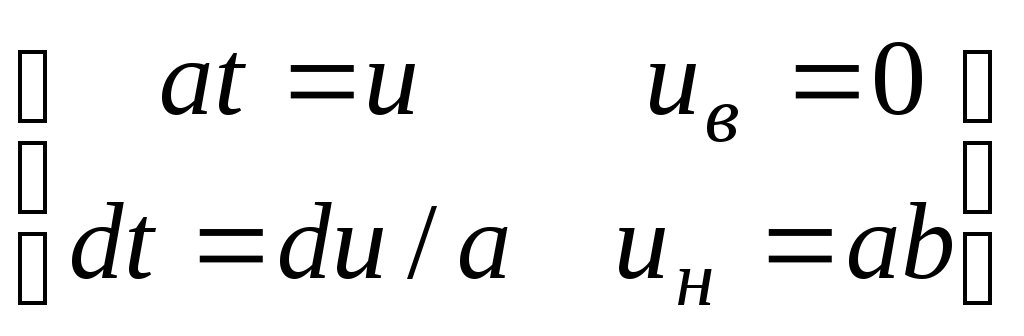F(
)
Пр.6
sin at
=:
=
;
cos at
=:
=
Теорема смещения. Переход в изображении от p к (p + z), где z комплексное число, причем Re (p + z) > s0 , приводит к дополнительному умножению оригинала на экспоненту e-zt
F(p + z) =: e-zt f(t) ( 3 )
Доказательство.
e-zt
f(t)
=:
=
= F(p
+ z)
Пр.7
ezt
sin
at
=:
; ezt
cos at
=:
Теорема
запаздывания.
Уменьшение параметра t
в оригинале на величину
>
0 приводит к дополнительному умножению
изображения на экспоненту
f(t
-
)
(t-
)
=:
F(p)
( 4 )
Доказательство.
f(t
-
)
=:
=
+
+
Первый
интеграл равен 0, т.к.
(t-
)
= 0 при t
<
.
f(t
-
)
=:
=
=
=
=
F(p)
Пр.8
(t
-
)
=:
и (t
– a)
(t
- а) =:
с учетом Пр. 5 .