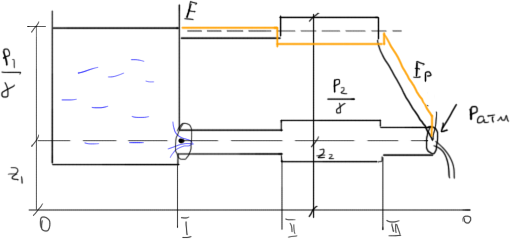
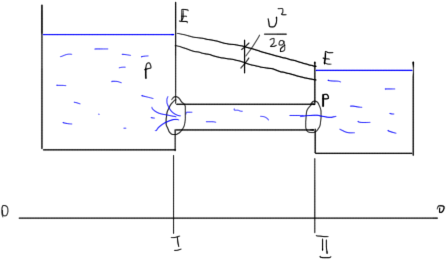
Построение пьезометрических линий
Режимы движения жидкости
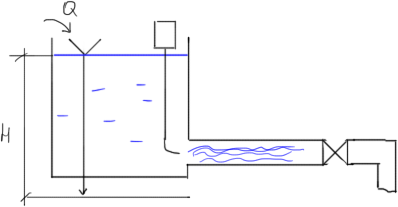
Опыты проводились при постоянном напоре и было установлено, что при малых скоростях подкрашивающая жидкость двигалась по определенной траектории, не перемешиваясь. Когда скорость увеличивалась, наблюдалось хаотичное движение. Таким образом, поток движения жидкости в трубке может характеризоваться на:
-
Ламинарный (параллельный)
-
Турбулентный (беспорядочный)
Основным
критерием для определения режима
движения жидкости служит безразмерный
параметр
(число Рейненса). Для закрытых потоков:
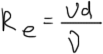
Число, при котором ламинарный режим переходит в турбулентный, и наоборот носит название критическое число Рейненса, и для закрытых потоков это число берется 2320. Для упрощения решения задач можно принимать это число равным 2500.
Если это число меньше критического, то режим ламинарный. Если больше – то режим турбулентный.
Скорость, соответствующая критическому числу называют критической скоростью.
При безнапорном движении для открытых потоков число Рейенса определяется:
,
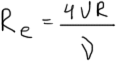где R - гидравлический
радиус.
Задача на тему режима движения жидкости.
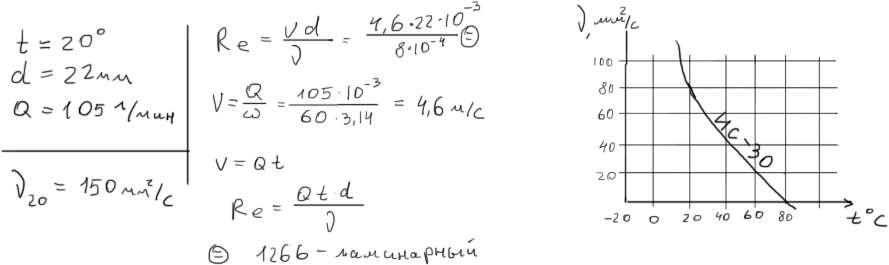
Гидравлическое сопротивление
Решение многих практических задач в гидравлике сводится к установлению зависимости, определяющей изменение скорости и давления по длине потока.
До этого мы польлзовались двумя уравненими:
-
-
Уравнение Бернулли:
-
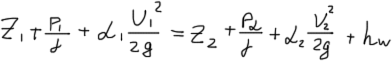
Используют зависимость от потерь напора в скорости и ряда других факторов.
Потери
напора вызываются сопротивлениями двух
видов: потери напора по длине
(
)
и местное сопротивление.
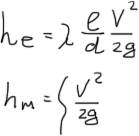
Коэффициент гидравлического трения и к пси – безразмерные коэффициенты, и зависят от ряда факторов:
-
От режима движения жидкости
-
От шероховатости стенок
-
От вида сопротивления.
Распределение скоростей и потерь напора при ламинарном движении.
Рассмотрим трубу, в которой движется жидкость.
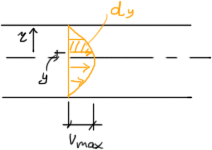
При ламинарном режиме потока слои жидкости движутся параллельно друг другу. Теоретически закон распределения скоростей по живому сечению потока с ламинарным режимом в трубопроводе выражается формулой:
И – гидравлический уклон
Гамма
Ню – коэффициент динамической вязкости
Эр – радиус трубы
Игрик – слой жидкости, который движется на расстоянии y от оси.
Таким образом скорости распределяются в трубе по закону параболы с максимумом на ее оси, таким образом средняя скорость будет равна:
Потери напора при ламинарном режиме определяются по формуле:
Распределение скоростей и потери напора при турбулентном режиме
При турбулентном режиме скорость движения в каждой точке потока постоянно изменяется по величине и направлению, колеблясь от одного какого либо значения, и называется осредненной местной скорость.
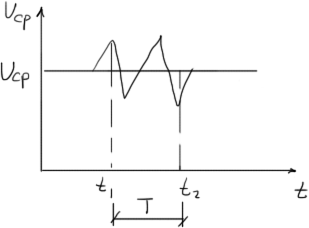
Если остаются неизменными во времени осредненные скорости, то турбулентное движение считают установившимся.
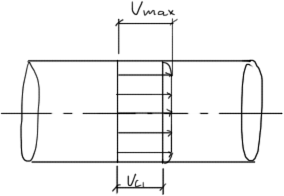
Осредненные скорости в данных точках практически постоянны и направлены вдоль оси потока. Поэтому при турбулентном режиме движения жидкости условно можно рассматривать как параллельно - струйное. Теоретических решений распределения скоростей по сечению потока и определения потерь напора для турбулентного режима нет.
Однако немецкий ученый Прандтль создал полуэмпирическую теорию турбулентности, в основу которой положена условная схема разделения жидкости в трубе на турбулентное ядро в центре и ламинарный слой по периметру.
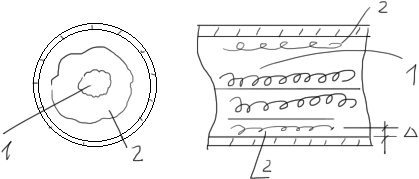
По мере увеличения скорости турбулентное ядро увеличивается.
Полученное по этой полуэмпирической теории турбулентности распределение скоростей выражается по формуле:
–
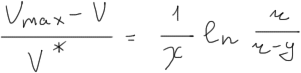
постоянная Прандтля = 0,4
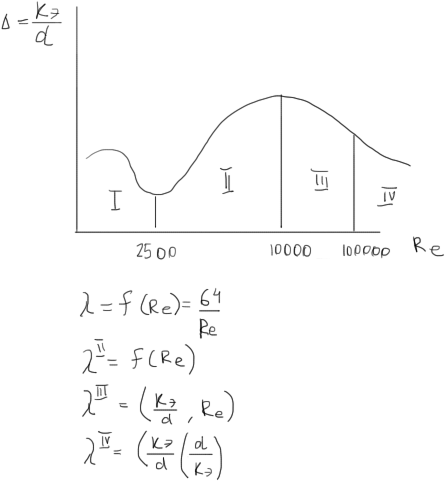
3 – переходная зона, в этом случае коэффициент гидравлического трения зависит от коэффициента шероховатости и числа Рейнедса.
4- квадратичная зона (турбулентный режим) – от к. шероховатости
Если диаметр труб составляет до 50 мм, то применяют термин относительной гладкости, если больше – то относительная шероховатость.