Физические основы оптических систем связи

Лекция 1

Вопросы

1. Геометрическая (лучевая) оптика

2. Принцип Ферма

3. Основные определения

1. Геометрическая (лучевая) оптика

С помощью волновой теории мы можем решать задачи о распространении света как в однородной среде, так и через любую оптическую систему, т. е. через совокупность различных сред, ограниченных теми или иными поверхностями и диафрагмами.

В вопросе о формировании светового пучка (светотехника) и в вопросах об образовании изображения (оптотехника), решение можно получить гораздо более простым путем, с помощью представлений геометрической оптики.

Геометрическая оптика оперирует понятием отдельных световых лучей, подчиняющихся известным законам преломления и отражения и независимых друг от друга

Понятие светового луча можно получить из рассмотрения реального светового пучка в однородной среде, из которого при помощи одной или последовательности диафрагм с отверстиями выделяется узкий параллельный пучок. Неизбежное угловое расширение реального светового пучка, пропущенного через диафрагму диаметра D, определяется углом дифракции φ ~ k/D (направление на 1-й диф. минимум). Только в предельном случае, когда λ = 0, подобное расширение не имело бы места, и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление распространения световой энергии. Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и геометрическая оптика есть лишь предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны.

В реальной оптике, где λ – конечная величина, отступления от законов геометрической оптики должны быть тем меньше, чем больше размеры D.

При относительно небольших расстояниях от объекта до точки наблюдения (дифракция Френеля) ширина области вблизи геометрической тени, где наблюдаются дифракционные полосы, примерно равна радиусу первой зоны Френеля; в случае плоской волны (бесконечно удаленный источник) радиус этой зоны (f – расстояние от объекта, вызвавшего дифракцию света, до точки наблюдения). За меру резкости тени естественно принять отношение линейного размера объекта х к радиусу зоны, т. е. х/r. Лишь при область полутени будет относительно очень широкой, и подобие объекта и тени нарушится. Из этого соотношения следует, что отсутствие тени будет лишь при расстояниях . Уже при х = 1 см, λ = 500 нм имеем f = 200 м.

2. Принцип Ферма

Когда справедлив переход к геометрической оптике, т. е. в случае исчезающе малой длины волны, распространение волнового фронта может быть найдено простым построением. Пусть поверхность F (рис. 1.) изображает поверхность равной фазы (волновой фронт) к некоторому моменту t. В каждой точке М этой поверхности построим сферу с радиусом dn = vτ, где v есть скорость распространения волны в данном месте, а τ – бесконечно малый промежуток времени. Поверхность F’, огибающая эти маленькие сферы, есть также поверхность равной фазы, ибо все точки ее будут иметь к моменту (t + τ) те же фазы, что и точки поверхности F к моменту t. Отрезки прямых dn, соединяющие точки М с точкой касания соответствующей сферы и огибающей, представляют собой элементы луча, перпендикулярные к поверхности фронта (случай изотропной среды, когда луч и нормаль к фронту совпадают).

Рис.1

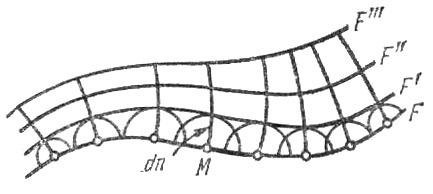
Действительный путь распространения света (луч) есть путь, для прохождения которого свету требуется мини-мальное время по сравнению с любым другим мыслимым путем между теми же точками (рис.2).

От точки А до точки В вдоль луча свет проходит за время , где , т. е. .

Рис.2

Всякий же другой мыслимый путь будет состоять из отрезков, для прохождения которых потребуется время τ_i, если этот отрезок совпадает с нормалью к фронту, или время, большее τ_i если отрезок отличается от нормали. Таким образом, действительный путь распространения света (луч) соответствует минимальному времени распространения.

Эта теорема, доказанная нами для волновой теории в том приближении, когда справедлива геометрическая оптика (λ → 0), представляет в геометрической оптике аксиому, именуемую принципом кратчайшего оптического пути (или минимального времени распространения). Она была сформулирована Ферма как общий закон распространения света (принцип Ферма, около 1660 г.). Для однородной среды этот принцип приводит к закону прямолинейного распространения согласно геометрической аксиоме о том, что прямая есть кратчайшее расстояние между двумя точками; для случая же перехода через границу различных сред этот принцип дает законы отражения и преломления света.

Пусть свет, исходя из точки Р, приходит в точку Q, преломляясь на плоской границе раздела двух сред (рис. 3). Проведем через Р и Q плоскость нормально к границе раздела (плоскость падения). Любой путь PO₁Q, лежащий вне плоскости падения, проходится светом за большее время, чем путь POQ, проведенный в плоскости падения так, чтобы О явилось следом перпендикуляра, опущенного из О₁, на плоскость падения.

Итак, в согласии с принципом Ферма путь, требующий минимального времени, должен лежать в плоскости падения (первый закон преломления). Для того чтобы из всех путей от Р до Q, лежащих в плоскости падения, выбрать путь, требующий минимального времени, исследуем, как меняется это время в зависимости от положения точки О на линии пересечения плоскости падения и плоскости раздела.

Рис.3

Положение точки О определено длиной отрезка АО = х, где А – след перпендикуляра, опущенного из Р на плоскость раздела.

Время распространения света по пути POQ есть 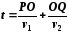, где v₁ и v₂ – скорости света в первой и во второй средах. Обозначив РА = h₁, QB = h₂ и AВ = р, найдем, что .

Условие, определяющее, при каком значении х это время будет минимально, есть равенство нулю . Из него следует

т.е.

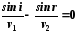
или .

Таким образом, из принципа Ферма вытекает закон преломления световых лучей. Аналогично можно рассмотреть задачу об отражении.