Определение длины волны с помощью колец Ньютона (Определение радиуса кривизны линзы)
1. В чем отличие геометрической и оптической разности хода?
Геометрическая разность хода интерферирующих волн — разность расстояний от источников волн до точки их интерференции.
Оптическая разность хода (произведение геометрической разности хода волн на показатель преломления среды)
∆ = xd/l.
В зависимости от того, целому или полуцелому числу длин волн равна оптическая разность хода, на тех или иных расстояниях х на экране наблюдаются светлые и темные полосы, параллельные друг другу. Расстояние между двумя соседними максимумами или минимумами освещенности называется шириной интерференционной полосы
∆x = lλ0/d ,где λ0 – длина волны монохроматического света.
2. Как использовать наблюдаемые явления для измерения столь малых величин, как длина волны света?
Рассмотрим плоскопараллельную пленку с показателем преломления n и толщиной d. Направим на пленку под углом i монохроматический свет. В точке падения О луч делится на два: часть света (луч 1) отразится от поверхности пленки, а часть войдет в пленку и преломится. Преломленный луч, дойдя до второй поверхности пленки, отразится от нее в точке С и, дойдя до точки В на верхней поверхности, выйдет из пленки под углом i (луч 2)
Лучи 1 и 2 когерентны, поэтому, если на их пути поставить собирающую линзу Л, то они сойдутся в одной из точек Р фокальной плоскости линзы и дадут интерференционную картину, которая будет определяться оптической разностью хода между интерферирующими лучами.
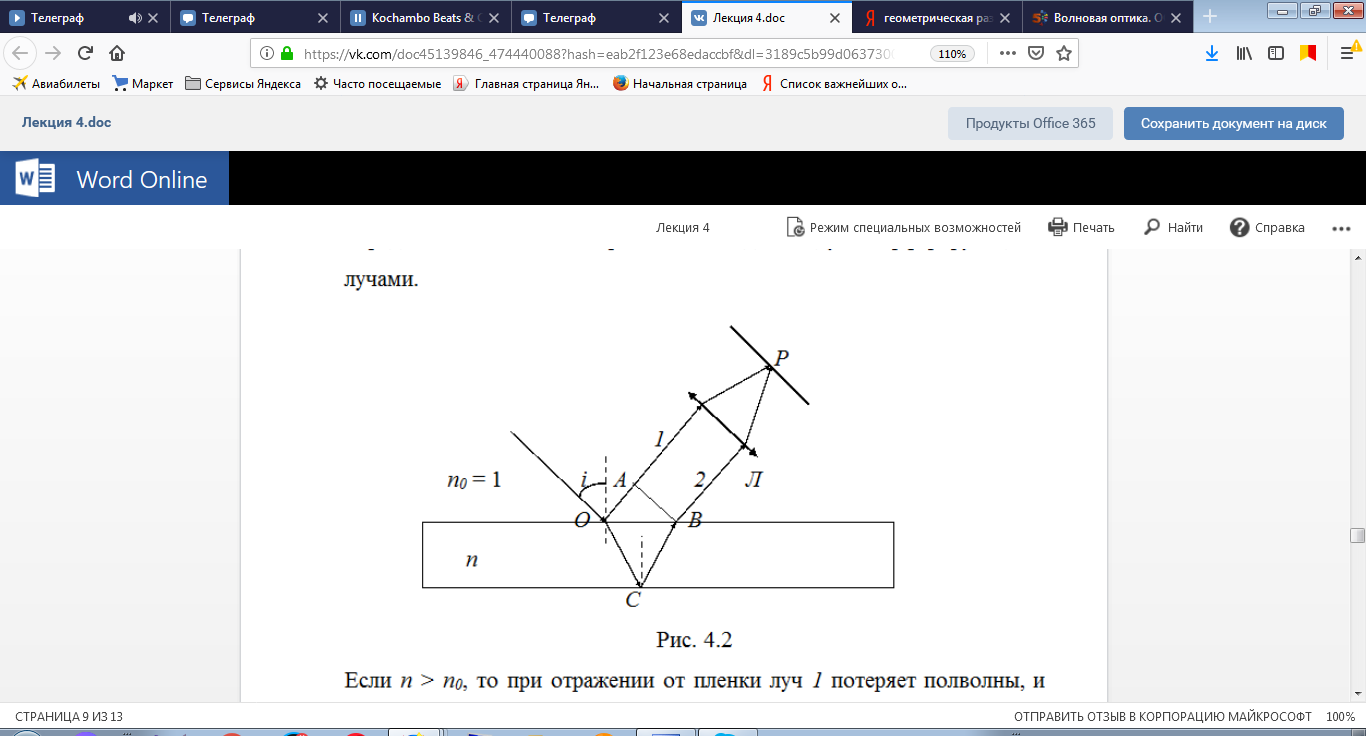
Если n > n0, то при отражении от пленки луч 1 потеряет полволны, и тогда оптическая разность хода
∆ = 2d(n2 – sin2i)1/2 + λ0/2. (4.12)
В точке Р будет максимум освещенности, если ∆ = mλ0, и минимум освещенности, если ∆ = (2m + 1)λ0/2 при m = 0, 1, 2,… Из выражения 4.12 следует, что интерференционная картина в тонкой плоскопараллельной пластинке определяется значениями d, n, i и λ0. Для каждого угла падения будет своя интерференционная полоса, поэтому для совокупности параллельных лучей, падающих на пластинку, возникнет совокупность полос равного наклона.
3. Схема установки и ход лучей при наблюдении колец Ньютона.
Примером полос равной толщины являются
кольца Ньютона. Они наблюдаются при
отражении света от границ воздушного
зазора, образованного плоскопараллельной
стеклянной пластинкой и соприкасающейся
с ней плосковыпуклой линзой с большим
радиусом сферической поверхности (рис.
4.3). Параллельный пучок света, падающий
нормально на плоскую поверхность линзы,
проходит ее без преломления, частично
отражается от верхней и нижней границ
воздушного зазора d. При наложении двух
отраженных лучей возникают полосы
равной толщины, представляющие собой
концентрические окружности.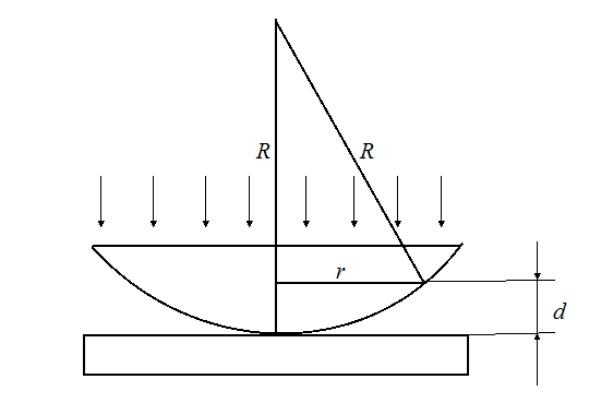
В отраженном свете оптическая разность хода
∆ = 2d + λ0/2
4. Получить формулу для радиуса кольца Ньютона? (Этот вопрос является обязательным).
В отраженном свете оптическая разность хода
∆ = 2d + λ0/2,
поскольку показатель преломления воздуха равен 1, а угол падения равен нулю. Из рис. видно, что R2 = (R – d)2 + r2, где R – радиус кривизны линзы, а r – радиус окружности, всем точкам которой соответствует одинаковый зазор d. Поскольку d мало, получаем, что d = r2/2R, тогда оптическая разность хода
∆ = r2/R + λ0/2, (4.14)
Радиус светлых колец может быть найден из выражения
rm(св) = [(m – 1/2)λ0R]1/2,
при m = 1, 2, 3,…, а радиус темных колец
rm(т)= (mλ0R)1/2
при m = 0, 1, 2,… Зная радиус кривизны сферической поверхности линзы и измеряя радиусы соответствующих колец, можно найти длину волны падающего на линзу света или при известной длине волны определить R.
Определение фокусных расстояний линз