Курсовые работы / расчет устойчивости системы
.doc4 РАСЧЕТ УСТОЙЧИВОСТИ СИСТЕМЫ
Для расчета устойчивости системы необходимо найти общую передаточную функцию. Для этого преобразуем структурную схему, предварительно разбив ее на участки:
Рисунок 1- Структурная схема ЛСУ
Передаточная функция для 1 участка:
Передаточные функции для 2 и 3 участков будут равны W1=W2=W3
Преобразуем параллельно соединенные звенья структурной схемы:
В результате получаем схему:
Рисунок 2- Преобразованная структурная схема САУ
Исследуем устойчивость САУ с помощью критерия Найквиста в Matlab:
w=tf([585.78 12300000000000],[0.000000966 20300 8430000 38500000 937000 2500 5850])
Transfer function:
585.8 s + 1.23e013
--------------------------------------------------------
9.66e-007s^6+20300s^5+8.43e006 s^4+3.85e007s^3+937000 s^2+2500 s+5850
Рисунок 3- Годограф Найквиста
По полученному годографу Найквиста видно, что при изменении частоты от 0<ω<∞ годограф не охватывает точку с координатами (-1; j0), следовательно система устойчива.
Построим график переходного процесса для этой системы. Переходный процесс-это реакция системы на единичное воздействие, то есть на единичную функцию Хевисайда l(t).
Рисунок 4- График переходного процесса
Определим из графика переходного процесса характеристики. Установившееся значение регулируемого параметра h(∞)=1000. Время регулирования tр=3 с.
Сравнивая время регулирования полученное из графика tр=3 с. и время регулирования заданное в техническом задании t=60 мин. можно увидеть, что разница между ними составляет более 5% и можно сделать вывод о необходимости применения корректирующего устройства.
Построим амплитудо-частотную характеристику системы при помощи программы Matlab, выполнив команду impulse(w). График амплитудо-частотной характеристики приведен на рисунке 5.
Рисунок 5- Амплитудо-частотная характеристика
Согласно графику
A(0)=0;
Amax(ω)=2*108.
Резонансная частота ωр=55
Гц; полоса пропускания 29<ωпр<72.5;
период колебаний
Проведем z-преобразование и проверим устойчивость системы по критерию Шур-Кона.
Дана передаточная
функция:
Разложим передаточную функцию
для облегчения z-преобразования:
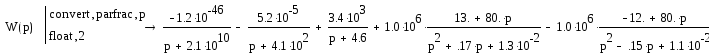
Проведем преобразование первого члена ряда:
Проведем преобразование второго члена ряда:
Зададим период дискретности и тактовую частоту:
Проведем преобразование третьего члена ряда:
Проведем преобразование четвертого члена ряда:
Разложим четвертый член для проведения z-преобразования:
Проведем преобразование пятого члена ряда:
Тогда общая передаточная функция после z-преобразования будет иметь вид:
