Термодинамические процессы в идеальных газах

Термодинамика изучает пять основных процессов идеальных газов:

1. изохорный, (v= const) происходящий при постоянном объеме газа;

2. изобарный, (р = const) происходящий при постоянном давлении;

3. изотермический, (Т = const) происходящий при постоянной темпера­туре;

4. адиабатный, (q = 0) протекающий без подвода или отвода теплоты, т.е. протекающий без теплообмена с окружающей средой;

5. политропный — обобщенный процесс изменения всех параметров рабочего тела при наличии теплообмена; для него четыре предыдущих процесса являются частными случаями.

1. Изохорный процесс

Изохорический или изохорный процесс (от др.-греч. ίσος — «равный», и χώρος — «пространство, занятое место») — это термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.При изохорическом процессе давление идеального газа прямо пропорционально его температуре. В реальных газах закон Шарля не выполняется.

На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T (температура), V (объем) и P (давление).

Термодинамика процесса

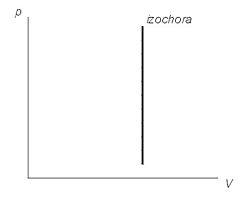
График изохорного процесса на диаграмме (P,V)

Из определения работы следует, что изменение работы при изохорном процессе равно:

Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:

,

Но такой интеграл равен нулю. Итак, при изохорном процессе газ работы не совершает:

.

Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю.Изменение внутренней энергии идеального газа можно найти по формуле:

,

где i — число степеней свободы, которое зависит от количества атомов в молекуле (3 для одноатомной (например, неон), 5 для двухатомной (например, кислород) и 6 для трёхатомной и более (например, молекула водяного пара)).

Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:

,

где  — молярная теплоёмкость при постоянном объёме.

Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:

Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:

,

то есть вся теплота, которую получает газ идёт на изменение его внутренней энергии.

Энтропия при изохорном процессе

Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует:

Выше была выведена формула для определения количества теплоты. Перепишем ее в дифференциальном виде:

,

где ν — количество вещества,  — молярная теплоемкостью при постоянном объеме. Итак, микроскопическое изменение энтропии при изохорном процессе можно определить по формуле:

Или, если проинтегрировать последнее выражение, полное изменение энтропии в этом процессе:

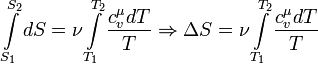
В данном случае выносить выражение молярной теплоемкости при постоянном объеме за знак интеграла нельзя, поскольку она является функцией, которая зависит от температуры.