
ТЕСТ
ПО «ЛОКАЛЬНЫМ СИСТЕМАМ УПРАВЛЕНИЯ»
для специальности «Управление и
информатика в технических системах»5 Вариантов по 15 вопросов
Указание: все задания имеют 4 варианта ответа, из которых правильный только один. Номер выбранного ответа обведите кружочком в бланке для ответов.
Вариант 3.
1. Критерий устойчивости Раусса.
1) Является алгебраическим критерием и позволяет по коэффициентам характеристического уравнения замкнутой системы определить место нахождения корней без решения характеристического уравнения. Критерий Раусса представляет собой правило, оформленное в виде таблицы, при этом коэффициенты уравнения, имеющие четные индексы записываются в первую строку, имеющие нечетные индексы- во вторую строку, остальные строки которых всего (n+1) и столбцы таблицы заполняются по предыдущим известным строкам на основе определенного правила.
2) Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то исходная система, описываемая нелинейными уравнениями устойчива. При этом никакие отброшенные при линеаризации члены второго и высших степеней отклонения, переменных не могут изменить устойчивость системы.
3) Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то исходная система неустойчива, при этом никакие отброшенные при линеаризации второй или выше степеней отклонения переменных не могут придать системе устойчивость.
4) Если характеристическое уравнение линеаризованной системы имеет хотя бы один вещественный корень или пару чисто мнимых сопряженных корней, то поведение действительной системы не может определяться его линеаризованным уравнением. Линеаризованная система находится на границе устойчивости и отброшенные при линеаризации уравнения члены второй или выше степеней отклонения переменных, коренным образом изменяют описание динамического процесса реальной системы.
2. Определение дискретной системы.
1) Системы у которых процессы и сигналы имеют конечное число значений по величине и времени.
2) Системы у которых процессы и сигналы имеют непрерывное значение по величине и времени.
3) Системы у которых процессы и сигналы имеют бесконечное число значений по величине и времени.
4) Не знаю.
3. Понятие импульсной системы.
1) Функциональная схема системы с цифровым регулятором

2) Линейной системой импульсного регулирования называется такая САР, которая кроме звеньев описываемых обыкновенными линейными ДУ содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.
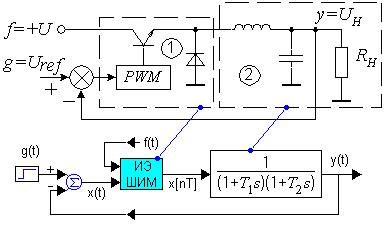
3)
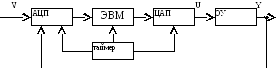
4)
4. Эквивалентная передаточная функция двузначной нелинейности.
1)
![]()
2)
![]()
3)
![]()
4) Не знаю.
5. Понятие логарифмической амплитудно-частотной характеристики системы.
1)
2
 )
)
![]()
3)

4)
![]()
6. Выражение для выходного сигнала при статической линеаризации нелинейного элемента.
1)
![]()
2)
![]()
3)
![]()
4) Не знаю.
7. Выражение для ошибки дискретной системы.
1)
![]()
2)
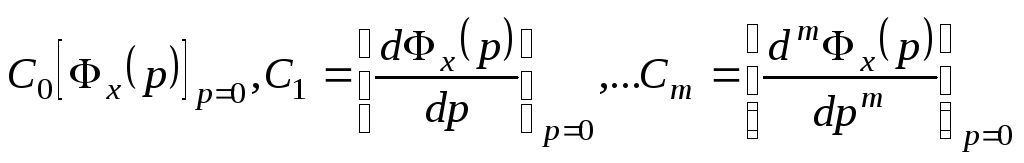
3)
![]()
4) Не знаю.
8. Проведение обратных билинейных преобразований.
1)
Чтобы восстановить непрерывный сигнал
из квантованного с помощью идеального
фильтра (ИФ) с прямоугольной частотной
характеристикой необходимо выполнение
соотношения:
![]() (аналитическая формулировка теоремы
Котельникова-Шеннона).
(аналитическая формулировка теоремы
Котельникова-Шеннона).
2)
Это преобразование позволяет получить
дискретную передаточную функцию
линейного объекта из его исходной
непрерывной передаточной функции:
![]() .
При малом шаге квантования справедлива
следующая замена переменной:
.
При малом шаге квантования справедлива
следующая замена переменной:![]() .
.
3)Используют -преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины , с помощью подстановки:
![]() .
.
4)
чтобы в системе были процессы минимальной
длительности, все собственные числа
матрицы A
должны быть равны 0,![]() ,
тогда характеристическое уравнение
системы принимает вид:
,
тогда характеристическое уравнение
системы принимает вид:![]()
9. Понятие наблюдаемости.
1) Процесс g(t) называется наблюдаемым, если каждая переменная состояния процесса обуславливает изменение некоторых выходных переменных.
2) Процесс g(t) называется наблюдаемым, если переменная состояния процесса обуславливает изменение некоторых выходных переменных.
3) Процесс g(t) называется наблюдаемым, если переменная состояния процесса обуславливает изменение каждой из выходных переменных.
4) Не знаю.
10. Схема последовательно-параллельного соединения звеньев.
1 )
)
2 )
)

3)

4)
11. Устойчивость нелинейной системы.
1)
Система называется асимптотически
устойчивой, если при движении из начальных
условий выполняется свойство:
![]() .
.
2)
Система называется асимптотически
неустойчивой, если при движении из
начальных условий выполняется свойство:
![]() .
.
3)
Система называется асимптотически
устойчивой, если при движении из начальных
условий не выполняется свойство:
![]() .
.
4)
Система называется асимптотически
устойчивой, если при движении из начальных
условий выполняется свойство:
![]()
12. Критерий устойчивости Михайлова.
1)
САР будет устойчивой, если изменении w
от 0 до +![]() вектор
Д(jw)
начав движение из точки, лежащей на
положительной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
вектор
Д(jw)
начав движение из точки, лежащей на
положительной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
2)
САР будет устойчивой, если изменении w
от 0 до +![]() вектор
Д(jw)
начав движение из точки, лежащей на
отрицательной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
вектор
Д(jw)
начав движение из точки, лежащей на
отрицательной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
3 )
САР будет устойчивой, если измененииw
от 0 до +
)
САР будет устойчивой, если измененииw
от 0 до +![]() вектор
Д(jw)
начав движение из точки, лежащей на
отрицательной вещественной полуоси
комплексной плоскости, вращаясь по
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
вектор
Д(jw)
начав движение из точки, лежащей на
отрицательной вещественной полуоси
комплексной плоскости, вращаясь по
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
4)
САР будет неустойчивой, если изменении
w
от 0 до +![]() вектор
Д(jw)
начав движение из точки, лежащей на
положительной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
вектор
Д(jw)
начав движение из точки, лежащей на
положительной вещественной полуоси
комплексной плоскости, вращаясь против
часовой стрелки, и нигде не обращаясь
в 0, обходит последовательно n
квадратов комплексной плоскости, где
n-
степень характеристического уравнения.
13. Понятие времени регулирования системы.
1)
Время регулирования
![]() – это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины
– это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины![]() от
ее установившегося значения
от
ее установившегося значения![]() будут
больше наперед заданного значения
будут
больше наперед заданного значения![]() .
.
2)
Время регулирования
![]() – время, за которое регулируемая величина
впервые достигает установившегося
значения.
– время, за которое регулируемая величина
впервые достигает установившегося
значения.
3) Время регулирования определяет быстродействие переходного процесса.
4)
Время регулирования
![]() – это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой
величины
– это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой
величины
![]() от
ее установившегося значения
от
ее установившегося значения![]() будут
меньше наперед заданного значения
будут
меньше наперед заданного значения![]() .
.
14. Передаточная функция последовательного соединения звеньев.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
15.Критерий устойчивости Найквиста.
1)
Если
система устойчива в разомкнутом
состоянии, то для устойчивости замкнутой
системы необходимо и достаточно, чтобы
АФХ разомкнутой системы для частоты
w
, изменяющейся от
0
до
![]() не охватывает точку с координатами(-1,
j0).
не охватывает точку с координатами(-1,
j0).
2)
Если
система устойчива в замкнутом состоянии,
то для устойчивости разомкнуто й системы
необходимо и достаточно, чтобы АФХ
разомкнутой системы для частоты
w
, изменяющейся от
0
до
![]() не охватывает точку с координатами(-1,
j0).
не охватывает точку с координатами(-1,
j0).
3)
Если
система устойчива в разомкнутом
состоянии, то для устойчивости замкнутой
системы необходимо и достаточно, чтобы
АФХ разомкнутой системы для частоты
w
, изменяющейся от
0
до
![]() не охватывает точку с координатами(1,
j0).
не охватывает точку с координатами(1,
j0).
4)
Если
система устойчива в замкнутом р состоянии,
то для устойчивости разомкнутой системы
необходимо и достаточно, чтобы АФХ
разомкнутой системы для частоты
w
, изменяющейся от
0
до
![]() не охватывает точку с координатами(1,
j0).
не охватывает точку с координатами(1,
j0).
16. Способ Гаусса — Зайделя.
1)
Способ заключается в изменении
координат у1,
. . ., уп.
Сначала
фиксируются все координаты у2,
. . .,
уп,
а
координата уi
изменяется
так, чтобы обратилась в нуль соответствующая
составляющая градиента
![]() .
Затем
изменяется координата у2
при
фиксированных остальных координатах
до обращения в нуль
.
Затем
изменяется координата у2
при
фиксированных остальных координатах
до обращения в нуль
![]() и т. д. После изменения координаты уn
обращаются
опять к у1
и
далее повторяют весь цикл снова. Этот
процесс продолжают до тех пор, пока не
будет достигнута точка экстремума FЭ.
и т. д. После изменения координаты уn
обращаются
опять к у1
и
далее повторяют весь цикл снова. Этот
процесс продолжают до тех пор, пока не
будет достигнута точка экстремума FЭ.
2)
Способ
заключается в поочередном изменении
координат у1,
. . ., уп.
Сначала
фиксируются все координаты у2,
. . .,
уп,
а
координата уi
изменяется
так, чтобы обратилась в нуль соответствующая
составляющая градиента
![]() .
Затем
изменяется координата у2
при
фиксированных остальных координатах
до обращения в нуль
.
Затем
изменяется координата у2
при
фиксированных остальных координатах
до обращения в нуль
![]() и т. д. После изменения координаты уn
обращаются
опять к у1
и
далее повторяют весь цикл снова. Этот
процесс продолжают до тех пор, пока не
будет достигнута точка экстремума FЭ.
и т. д. После изменения координаты уn
обращаются
опять к у1
и
далее повторяют весь цикл снова. Этот
процесс продолжают до тех пор, пока не
будет достигнута точка экстремума FЭ.
3)
Способ
заключается в изменении координат.
Сначала
фиксируются все координаты у2,
. . .,
уп,
а
координата уi
изменяется
так, чтобы обратилась в нуль соответствующая
составляющая градиента
![]() .
Затем
изменяется координата у3
при
фиксированных остальных координатах
до обращения в нуль
.
Затем
изменяется координата у3
при
фиксированных остальных координатах
до обращения в нуль
![]() и т. д.
и т. д.
4) Способ заключается в изменении координат у1, . . ., уп. После изменения координаты уn обращаются опять к у1 и далее повторяют весь цикл снова. Этот процесс продолжают до тех пор, пока не будет достигнута точка экстремума FЭ.
17. Способ наискорейшего пуска.
1) При способе наискорейшего спуска движение происходит по начальному направлению вектора градиента F до тех пор, пока производная функции F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной от F по этому направлению. Процесс повторяется до достижения точки экстремума.
2) При способе наискорейшего спуска движение происходит по конечному направлению вектора градиента F до тех пор, пока производная функции F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной
3) При способе наискорейшего спуска движение происходит к начальному направлению вектора градиента F до тех пор, пока производная функции F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной
При способе наискорейшего спуска движение происходит от срединного направления вектора градиента F до тех пор, пока производная функции F по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого вектора до обращения в нуль производной
18. Структурная схема прямого программирования.
1)
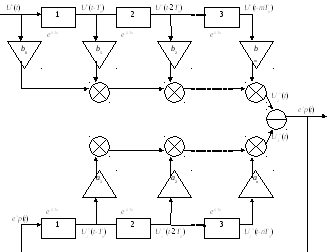
2)

3)

4) Не знаю.
19. Понятие наблюдаемости.
1) Процесс g(t) называется наблюдаемым, если каждая переменная состояния процесса обуславливает изменение некоторых выходных переменных.
2) Процесс g(t) называется наблюдаемым, если переменная состояния процесса обуславливает изменение некоторых выходных переменных.
3) Процесс g(t) называется наблюдаемым, если переменная состояния процесса обуславливает изменение каждой из выходных переменных.
4) Не знаю.
20. Понятие параллельного корректирующего устройства.
1) Параллельные КУ снижают частоту среза fср ЛСА и делают её малочувствительной к флуктуациям и помехам КУ данного типа, уменьшают влияние нелинейности во внутренних контурах системы.
2) Параллельные КУ повышают частоту среза fср ЛСА и делают её малочувствительной к флуктуациям и помехам КУ данного типа, уменьшают влияние нелинейности во внутренних контурах системы.
3) Параллельные КУ повышают частоту среза fср ЛСА и делают её нечувствительной к флуктуациям и помехам КУ данного типа, увеличивают влияние нелинейности во внутренних контурах системы.
4) Не знаю.
21. Понятие импульсного воздействия.
1)
Импульсное воздействие имеет форму
импульса длительностью
![]() и площадью импульса
и площадью импульса![]() :
:
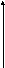
![]()








![]()


![]()
2)
Импульсное воздействие имеет форму
импульса длительностью
![]() и площадью импульса
и площадью импульса![]() :
:

![]()




3









 )
Импульсное воздействие имеет форму
импульса длительностью
)
Импульсное воздействие имеет форму
импульса длительностью![]() и площадью импульса
и площадью импульса![]() :
:
4)
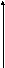









 Импульсное
воздействие имеет форму импульса
длительностью
Импульсное
воздействие имеет форму импульса
длительностью![]() и площадью импульса
и площадью импульса![]() :
:
22. Что такое автоколебания?
1) Автоколебания - колебания с постоянной амплитудой и частотой, возникающие в системе при отсутствии периодического сигнала на входе.
2) Автоколебания - колебания с постоянной амплитудой, возникающие в системе при отсутствии периодического сигнала на входе.
3) Автоколебания - колебания с постоянной частотой, возникающие в системе при отсутствии периодического сигнала на входе.
4) Автоколебания - колебания с постоянной амплитудой и частотой, возникающие в системе.
23. Устойчивость дискретной системы.
1) Чтобы линейная импульсная система была устойчивой достаточно чтобы модули собственных значений матрицы А были меньше единицы.
![]()
2) Линейная импульсная система устойчива, если все корни лежат в круге единичного радиуса.
3) Линейная импульсная система неустойчива, если все корни лежат в круге единичного радиуса.
4) Чтобы линейная импульсная система была неустойчивой достаточно чтобы модули собственных значений матрицы А были меньше единицы.
![]()
24. Критерий устойчивости Гурвица.
1) Условие устойчивости по Гурвицу сводится к тому, чтобы при a0>0 все диагональные миноры главного определителя были >0.
2) Если корни характеристического уравнения расположены на комплексной плоскости, то для устойчивости системы необходимо, чтобы все корни лежали слева от мнимой оси.
3) Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то исходная система неустойчива.
4) Чтобы САУ описываемая линейными дифференциальными уравнениями с постоянными коэффициентами была устойчивой, необходимо и достаточно, чтобы вещественные корни дифференциального уравнения были отрицательны.
