32. Статистическое распределение выборки.
32.1. Статистическое
распределение выборки имеет вид
Тогда
относительная частота варианты
,
равна …
4
0,25
0,3
0,2
32.2. Статистическое
распределение выборки имеет вид
Тогда
относительная частота варианты
,
равна …
0,5
0,2
0,65
0,5
32.3. Статистическое
распределение выборки имеет вид
Тогда
относительная частота варианты
,
равна …
0,5
10
0,1
0,2
32.4. Статистическое
распределение выборки имеет вид
Тогда
относительная частота варианты
,
равна …
0,5
0,3
0,55
6
32.5. Статистическое
распределение выборки имеет вид
Тогда
относительная частота варианты
,
равна …
0,3
0,4
6
0,1
33. Характеристики вариационного ряда.
33.1. Мода вариационного ряда 2 , 5 , 5 , 6 , 7 , 9 , 10 равна …
2
10
6
5
33.2. Мода вариационного ряда 5 , 8 , 8 , 9 , 10 , 11 , 13 равна …
9
8
13
9
33.3. Мода вариационного ряда 1 , 2 , 3 , 4 , 5 , 5 , 7 равна …
1
5
7
4
33.4. Мода вариационного ряда 1 , 2 , 5 , 6 , 7 , 7 , 10 равна …
1
10
6
7
33.5. Мода вариационного ряда 2 , 3 , 4 , 7 , 8 , 8 , 9 равна …
7
2
9
8
34. Точечные оценки параметров распределения.
34.1. Дана выборка
объема n.
Если каждый элемент выборки увеличить
на 5 единиц, то выборочное среднее
…
увеличится на 5 единиц
увеличится на 10 единиц
уменьшится на 5 единиц
не изменится
34.2. Дана выборка
объема n.
Если каждый элемент выборки уменьшить
на 8 единиц, то выборочное среднее
…
уменьшится в 4 раза
увеличится на 8 единиц
уменьшится на 8 единиц
не изменится
34.3. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 10, 11. Тогда несмещенная оценка математического ожидания равна…
8,4
8,2
9
10,25
34.4. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 13, 14, 15. Тогда несмещенная оценка математического ожидания равна…
12,2
12,4
15,25
13
34.5. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 12, 14, 16. Тогда несмещенная оценка дисперсии измерений равна…
8
0
4
3
35. Численные методы решения алгебраических уравнений.
35.1. Действительный
корень уравнения
принадлежит
интервалу…
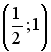
35.2. Действительный
корень уравнения
принадлежит
интервалу…
35.3. Три итерации
метода половинного деления при решении
уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в
точках...
35.4. Три итерации
метода половинного деления при решении
уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в
точках...
35.5. Три итерации
метода половинного деления при решении
уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в
точках...
36. Численные методы анализа.
36.1. Корень уравнения
равен
…
1
- 1
- 2
0
36.2. Корень уравнения
равен
…
- 5
3
5
4
36.3. Действительный
корень уравнения
принадлежит
интервалу…
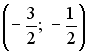
36.4. Действительный
корень уравнения
принадлежит
интервалу…
36.5. Действительный
корень уравнения
принадлежит
интервалу…
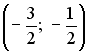
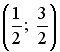
