7. Линейные операции над векторами.

7.1. Упрощение выражения  приводит его к виду …

7.2. Упрощение выражения  приводит его к виду …

7.3. Упрощение выражения  приводит его к виду …

7.4. Если система векторов  и  образует базис на плоскости, то…

обязательно отрицательно

может быть любым действительным числом

7.5. Если для двух ненулевых векторов  выполняется условие , то это равносильно условию…

и  коллинеарны

8. Скалярное произведение векторов.

8.1. Пусть  и  – взаимно перпендикулярные единичные векторы. Тогда  равно…

3

5

7

9

8.2. Если ,  и скалярное произведение , то векторы  и  образуют угол  при , равном…

- 32

9

64

8.3. Векторы  и  перпендикулярны при m, равном …

3,5

- 2

- 3,5

- 12

8.4. Векторы  и  перпендикулярны при m, равном …

2,5

- 2

2

- 1

8.5. Векторы   и   изображены на рисунке. Тогда их скалярное произведение   равно …

-

0

- 6

9. Функции: основные понятия и определения.

9.1. Пусть . Тогда сложная функция  нечетна, если функция  задается формулами…

9.2. Пусть . Тогда сложная функция  четна, если функция  задается формулами…

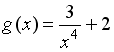
9.3. Пусть . Тогда сложная функция  нечетна, если функция  задается формулами…

9.4. Пусть . Тогда сложная функция  четна, если функция  задается формулами…

9.5. Пусть . Тогда сложная функция  четна, если функция  задается формулами…

10. Непрерывность функции. Точки разрыва.

10.1. Число точек разрыва функции, заданной на отрезке , график которой имеет вид равно …

3

10.2. Число точек разрыва функции, заданной на отрезке , график которой имеет вид равно …

3

10.3. Число точек разрыва функции, заданной на отрезке , график которой имеет вид равно …

5

10.4. Число точек разрыва функции, заданной на отрезке , график которой имеет вид равно …

1

10.5. Число точек разрыва функции, заданной на отрезке , график которой имеет вид равно …

2

11. Производные высших порядков.

11.1. Значение производной третьего порядка функции  в точке  равно…

0

1

4

8

11.2. Значение производной второго порядка функции  в точке  равно…

- 1

1

- 25

25

11.3. Значение производной второго порядка функции  в точке  равно …

0

6

9

1

11.4. Значение производной второго порядка функции  в точке  равно …

16

108

12

112

11.5. Производная второго порядка функции    имеет вид…

12. Приложения дифференциального исчисления фоп.

12.1. Наименьшее значение функции  на отрезке  равно … 1

12.2. Наименьшее значение функции  на отрезке  равно …

2

12.3. Наименьшее значение функции  на отрезке  равно …

5

12.4. Наибольшее значение функции  на отрезке  равно …

1

12.5. Наибольшее значение функции  на отрезке  равно …

3

13. Дифференциальное исчисление фнп.

13.1. Частная производная функции  по переменной  в точке  равна…

2

– 2

5

0

13.2. Частная производная функции  по переменной  в точке  равна…

0

13.3. Частная производная функции  по переменной  в точке  равна…

13.4. Частная производная функции  по переменной  в точке  равна…

13.5. Линиями уровня функции   являются …

прямые

параболы

эллипсы

гиперболы