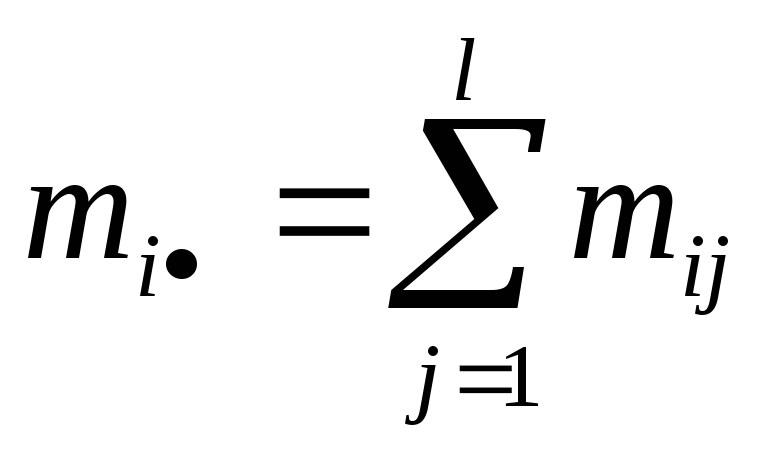14)Критерий хи-квадрат

Типы качественных признаков

Качественные признаки используют описательные средства для измерения или классификации объектов.

Качественныепризнаки отличаются от количественных тем, что над ними нельзя производить арифметические действия.

Качественные признаки подразделяются на номинальные и порядковые.

Номинальные признаки представлены категориями, для которых не определен никакой другой способ сравнения, кроме совпадения и несовпадения.

Примеры: пол, наличие болезней, цвет волос.

Номинальные признаки, которые могут быть отнесены только к двум противоположным категориям называютсядихотомическими.

Например: заболел – не заболел, есть эффект – нет эффекта.

Порядковые признаки представлены категориями, которые можно упорядочить в порядке возрастания или убывания признака.

Примеры.

а) оценивание знаний («отлично», «хорошо», «удовлетворительно», «плохо»)

б) градация званий в спорте (перворазрядник, КМС, МС)

д) категории отелей по «звездам»,

е) в экологии при измерении интенсивности выраженности определенных явлений.

Например, оценка состояния объекта в терминах «очень хорошо», «хорошо», «удовлетворительно», «плохо», «очень плохо».

Примеры: изменение цвета растительности при воздействии вредных выбросов какого-либо предприятия, переносимость условий обитания у человека.

КРИТЕРИЙ ОДНОРОДНОСТИ ДАННЫХ

Пусть имеется несколько независимых серий наблюдений, описывающих одно и то же явление, но полученные в разных условиях.

Требуется определить, являются ли эти выборки однородными по исследуемому признаку.

Это означает, что выборки взяты из одного и того же распределения.

H₀: данные однородны, нет зависимости от условий экспериментов.

15)Критерий независимости признаков

Рассмотрим результаты экспериментов, в которых наблюдения проводились за двумя признаками X и Y.

Признаки могут быть количественными и качественными.

Признаки в экспериментах имели следующие различные значения:

X: x₁, ,x₂,…,x_q

Y: y₁, y₂,…,y_l.

Обозначим - число экспериментов, в которых и .

Тогда результаты экспериментов можно представить в виде таблицы сопряженности признаков:

Y X	y1	y2	…	yl
x1	m11	m12	…	m1l
x2	m21	m22	…	m2l
…	…	…	…	…	…
xq	mq1	mq2	…	mql
			…		n

Число наблюдений nудовлетворяет условию

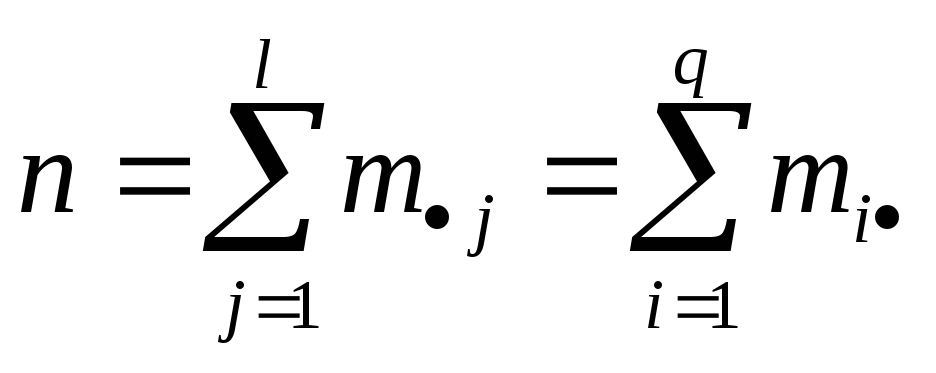(1)

Математическая постановка: - проверка гипотезы

H₀ :X и Y независимы.

Проверяется гипотеза при заданном уровне значимости .

В качестве статистического критерия выбирается критерий «хи-квадрат» или критерий Пирсона.

Выборочное значение критерия рассчитывается по формуле

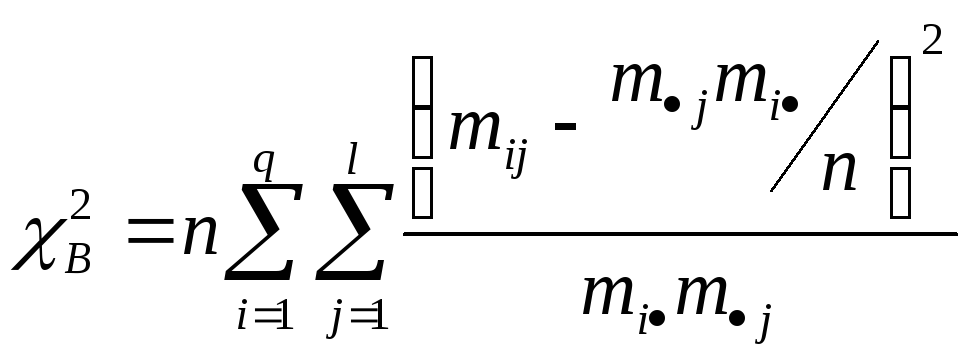(2)

Доказано, что при закон распределения случайной величины (2) независимо от того, какому закону подчинена генеральная совокупность, стремится к закону распределения Пирсона или к распределению («хи-квадрат»).

По расчетной формуле

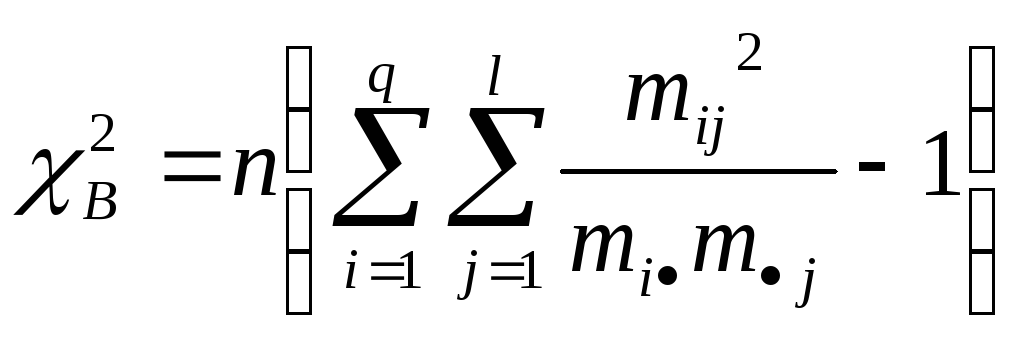(3)

Строим правостороннюю критическую область

где определяется по таблице 5 критических точек распределения по уровню значимости .

Число степеней свободы

; (4)

где q – число различных значений признака X,

l – число различных значений признака Y.

По таблице 5 определяем .

Сравниваем и :

если - нет оснований отвергнуть гипотезу , и признаки X и Y независимы.

если нулевая гипотеза отвергается, и признаки X и Y зависимы.

В примере 1 .

Тем самым, признаки зависимы. Это значит, что существует зависимость между психическим состоянием человека и полом.

Таблица сопряженности 2х2

Пусть признаки принимают по два альтернативных значения (дихотомические признаки):

признак X:

признак Y:

Таблица сопряженности примет вид

Y X
	m11	m12
	m21	m22
			n

Формула для расчета выборочного значения критерия (3) упрощается:

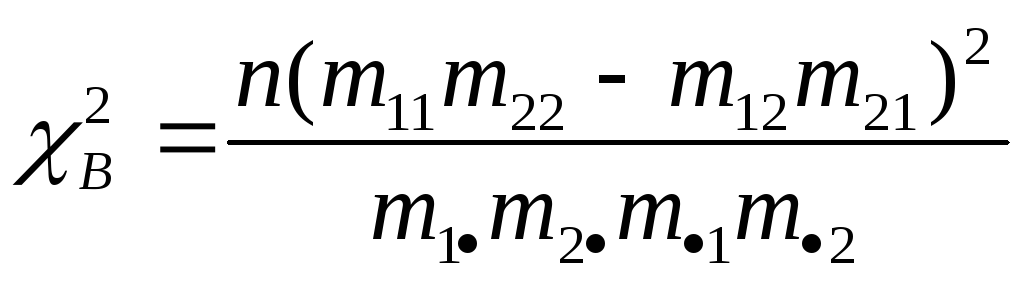(5)