4 Воздействие суммы гармонических колебаний на цепь с нелинейным элементом

4.1 Спектральный состав тока при бигармоническом воздействии

Бигармоническим воздействием называется сигнал, состоящий из суммы двух гармонических колебаний с различными частотами и и амплитудами и :

.

Спектр бигармонического сигнала изображен на рисунке 13, а.

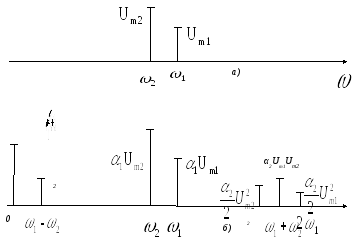
а) ―спектр бигармонического сигнала;

б) ―спектральный состав тока в цепи с нелинейным элементом

Рисунок 13― Спектры бигармонического сигнала

Пусть на вход нелинейного элемента, ВАХ которого аппроксимирована полиномом второй степени

Подано напряжение смещения и бигармонический сигнал . Подстановка напряжения в выражение для ВАХ позволяет определить ток в цепи нелинейного элемента в виде: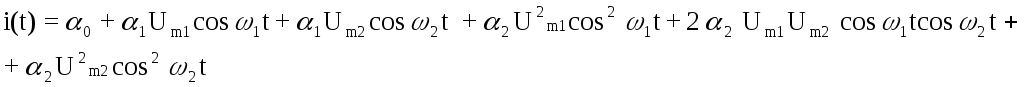

Используя тригонометрические формулы

и

Получим

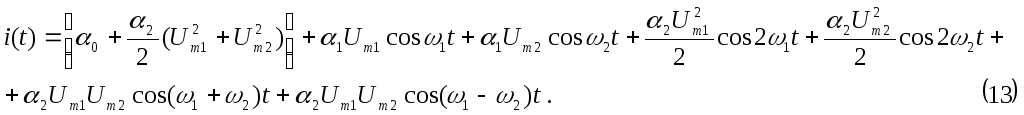
Спектральный состав тока в цепи с нелинейным элементом показан на рисунке 13, б.

Принципиально новым по сравнению с воздействием на нелинейный элемент одного гармонического колебания здесь является появление спектральных составляющих с комбинационными частотами и . Если ВАХ нелинейного элемента аппроксимирована в общем случае полиномом третьей степени, то в спектральном составе тока будут присутствовать составляющие с комбинационными частотами , причем , где и ―целые положительные числа (0,1,2,…). Так, при аппроксимации полиномом третьей степени в составе спектра присутствуют комбинационные частоты, приведенные в таблице 1.

4.2 Комбинационные частоты при воздействии суммы синусоидальных колебаний

В общем случае входное воздействие можно представить бесконечной суммой:

В зависимости от степени аппроксимирующего полинома (5) в спектре тока, протекающего через нелинейный элемент, появляются комбинационные частоты вида: ; ; ―целые положительные числа. Например, при воздействии на нелинейный элемент с ВАХ в виде полинома второй степени суммы трех гармонических колебаний в спектре тока помимо постоянной составляющей и первых двух гармоник каждой частоты будут присутствовать комбинационные частоты , , . При аппроксимации полиномом третьей степени дополнительно появляются третьи гармоники , , и комбинационные частоты типа , , и т.п.

Таблица 1

Значения	Частоты спектральных составляющих при значениях ρ
	0	1	2	3
0
1				―
2			―	―
3		―	―	―

4.3 Преобразователи частоты

При передаче электрических сигналов на расстояние часто требуется переносить спектр сигнала вверх или вниз по шкале частот. Такой перенос спектра называется преобразованием частоты. Необходимость в преобразовании частот возникает, например, когда спектр сигнала, который нужно передать, расположен на шкале частот значительно ниже полосы пропускания системы передачи.

В качестве преобразователя частоты может быть использован усилительный каскад на транзисторе с колебательным контуром (рисунок 14). Предположим, что нужно перенести вверх по шкале частот на величину гармоническое низкочастотное колебание с частотой : . Подадим на вход нелинейного резонансного усилителя кроме этого колебания также высокочастотное колебание с частотой : .

Рисунок 14―Усилительный каскад на транзисторе с с колебательным контуром

Амплитуды напряжения смещения , низкочастотного и высокочастотного колебаний выберем так, чтобы работать на участке ВАХ, который достаточно точно аппроксимируется полиномом второй степени:

. (14)

Напряжение на участке «база―эмиттер»

.

При подстановке выражения в зависимость в формуле для тока появляются в соответствии с формулой (13) гармонические колебания с частотами , , , и с суммарной и разностной комбинационными частотами и .

Колебательный контур резонансного усилителя настроен на частоту и выделяет из спектрального состава тока колебание . Выделенное колебание тока создает на резонансном сопротивление контура _. падение напряжения

.

которое и является выходным сигналом преобразователя частоты.

В реальных системах связи передаваемый низкочастотный сигнал не является гармоническим, а имеет сложный спектр (рисунке 15, а), т.е. состоит из суммы гармонических колебаний с частотами , , ,…

Если этот сигнал вместе с высокочастотным колебанием подать на нелинейный элемент, то в спектре тока (рисунок 15, б), протекающего через нелинейный элемент, будут присутствовать полезные продукты преобразования ― комбинационные частоты , , ,… Чтобы отфильтровать токи с этими частотами, недостаточно воспользоваться колебательным контуром, поскольку он не сможет обеспечить хорошую фильтрацию полезных продуктов преобразования. Его можно заменить в схеме рисунок 14 обычной резистивной нагрузкой, а на выходе системы включить электрический фильтр с характеристикой ослабления (на рисунке 15, б она показана штриховой линией), обеспечивающей необходимую степень подавления несущего колебания с частотой.

Приведем еще несколько практических схем преобразователей частоты. На рисунке 16 представлены диодные преобразователи: однократный (а), двукратный или балансный (б) и кольцевой (в), работающие в режиме больших амплитуд колебания частоты, т.е. в режиме аппроксимации ВАХ диодов линейно―ломаными функциями. Схема балансного транзисторного преобразователя частоты показана на рисунке 17.

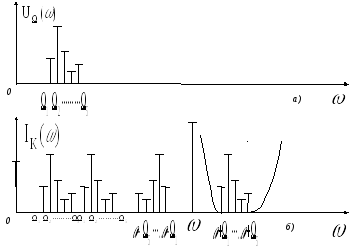
а) ―сложный спектр сигнала в реальных системах связи

б) ―спектр тока протекающего через нелинейный элемент при подаче низкочастотного и высокочастотного сигнала

Рисунок 15―спектры тока протекающего через нелинейный элемент при подаче различных сигналов

В балансных и кольцевых преобразователях гораздо меньше побочных продуктов преобразования; тем самым значительно облегчаются требования к фильтру, выделяющему полезные колебания.

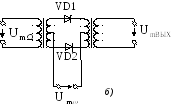
а) ―однократный; б) ―двукратный или балансный; в) ―кольцевой

Рисунок 16― диодные преобразователи

Рисунок 17―Схема балансного транзисторного преобразователя частоты

20