курсовая работа / Курсовик ТАУ / Чередников_TAU

ИСХОДНЫЕ ДАННЫЕ

Дана функциональная схема измерительной головки к внутришлифовальному станку

С труктурная схема этой системы управления имеет вид

где Q(t) – электрические сигналы,

X(t) – изменение диаметра отверстия,

У – система наружных и внутренних рычагов,

ПУ – рамка с пружинным параллелограммом, измерительным соплом и заслонкой,

ИУ – отсчетно-командное устройство,

ОР – станок,

Д – алмазные наконечники.

Принцип работы.

Алмазные наконечники (Д) прижимаются к обрабатываемой поверхности. При изменении диаметра отверстия сигнал проходит через систему наружных и внутренних рычагов (У) и попадает на рамку с пружинным параллелограммом, измерительным соплом и заслонкой (ПУ). Изменение давления в измерительной ветви, связанное с изменением зазора между измерительным соплом и заслонкой, преобразуется отсчетно-командным устройством (ИУ) в электрические сигналы для управления станком (ОР).

Передаточные функции каждого элемента системы:

ЗАДАНИЕ

1 Анализ линейной СУ: по данной структурной схеме системы управления (СУ) построить переходный процесс и частотные характеристики системы и по ним определить оценки качества СУ; исследовать систему на устойчивость; построить логарифмические характеристики и определить запасы устойчивости по фазе и амплитуде.

2 Анализ нелинейной СУ: осуществить преобразование нелинейной системы, линеаризацию нелинейного элемента; построить фазовый портрет.

1 АНАЛИЗ ЛИНЕЙНОЙ СУ

1.1. Упрощение структурной схемы.

W6(p) – передаточная функция прямой цепи.

Определим передаточные функции замкнутой цепи (системы в целом) и разомкнутой цепи. Соответственно

1.2. Частотные характеристики системы.

Приведем передаточную функцию системы к частотному виду.

Выделим действительную и мнимую части:

Определим вид амплитудочастотной и фазочастотной функций и построим их графики:

Рис. 2 Фазочастотная характеристика

1.3. Переходный процесс системы.

Определим вид функции переходного процесса.

1

Рис. 3 Переходный процесс

.4. Оценки качества системы.

1.4.1. Прямые оценки качества системы.

По полученному переходному процессу (рис. 3) определяем:

- перерегулирование: ;

- время регулирования: ;

- время достижения первого максимума: ;

- время первого согласования: ;

- период колебаний: ;

- колебательность: .

1.4.2. Косвенные оценки качества системы.

По рис. 1:

- резонансная частота: ;

- частота среза: ;

- полоса пропускания (частота при ): ;

- колебательность: .

1.5. Анализ устойчивости СУ.

Исследуем систему на устойчивость с помощью критерия устойчивости по Ляпунову. Система устойчива тогда, когда все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости.

Определим корни характеристического уравнения

Все корни находятся в левой полуплоскости комплексной плоскости. Следовательно, система устойчива.

1.6. Логарифмические характеристики системы. Определение запасов устойчивости.

Построим ЛАЧХ и ЛФЧХ разомкнутой системы (рис. 4).

И

Рис. 4 ЛАЧХ и ЛФЧХ системы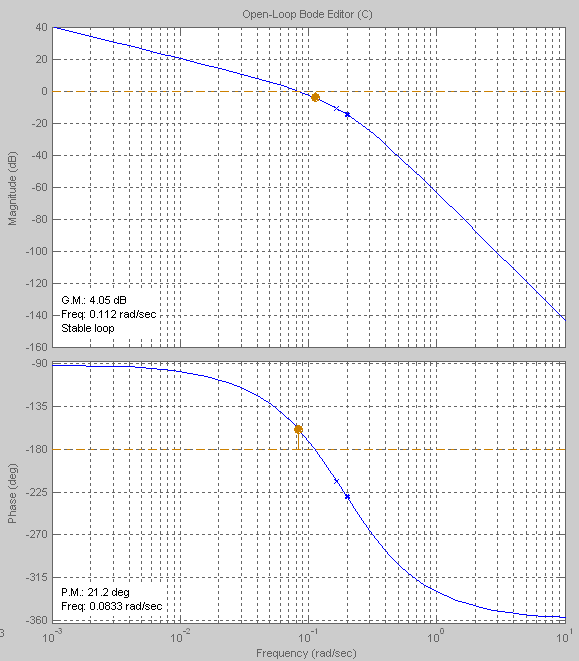

з рисунка видно, что запасы устойчивости по амплитуде и фазе составили 4,05 дБ и 21,2°, соответственно.

2 АНАЛИЗ НЕЛИНЕЙНОЙ СУ

В структурной схеме исходной системы вместо ПУ поставим нелинейный элемент с нелинейной характеристикой вида

(1)

Т огда структурная схема примет следующий вид

П реобразуем полученную структурную схему, разделив ее на линейную и нелинейную части.

Разорвем систему перед нелинейным элементом.

X

F(x)

W_лч(p)

X_i

u-X

- передаточная функция линейной части.

По определению передаточной функции

Следовательно:

Пусть на вход подано постоянное воздействие . Тогда перейдем от самих величин к их отклонениям относительно постоянного входного воздействия. Введем обозначения:

Получаем следующую систему уравнений

(2)

2.1. Построим фазовый портрет, используя систему уравнений (2) и (1). Пусть в начальный момент времени система выведена в точку с координатами (2;0).

Рис.6 Фазовый портрет

Переходный процесс нелинейной СУ

Рис.7 Переходный процесс нелинейной СУ

2.2. Линеаризация нелинейного элемента.

Произведем линеаризацию НЭ методом гармонической линеаризации (ГЛ).

Коэффициенты ГЛ для данного нелинейного элемента

Т. к. , то

.

Рассмотрим уравнение СУ:

(1)

Для НЭ имеем

. (2)

Подставляя (2) в (1), получим

Рассмотрим следующее уравнение:

(3)

В уравнении (3) сделаем замену: , - и выделим действительную и мнимую части.

Из системы уравнений (4) определим частоту и амплитуду:

ω=0.

Решим последнее уравнение графически.

П усть .

Из рис. 8 видно, что уравнение (5) не имеет решений. Следовательно, данный нелинейный элемент нельзя линеаризовать.

Заключение: до введения нелинейного элемента качество управления исходной СУ было хорошим, но требовала некоторой коррекции для уменьшения времени регулирования и перерегулирования; нелинейный элемент улучшил качество управления СУ (о чем свидетельствует фазовый портрет).

16