курсовая работа / Курсовик ТАУ / Трутнев

Балаковский институт техники, технологии и управления

Факультет инженерно-строительный

Кафедра Управление и информатика в технических системах

курсовая работа

по дисциплине

теория автоматического управления

анализ систем автоматического управления

Выполнил студент группы УИТ – 42

Трутнев Сергей Николаевич.

Проверила кандидат технических наук

Скоробогатова Татьяна Николаевна.

« » 2004

Балаково 2004.

Задание

Первая часть.

1. Выбрать для исследования линейную систему автоматического управления.

2. По принципиальной функциональной схеме выбранной системы составить структурную.

3. Определить передаточные функции элементов структурной схемы.

4. Преобразовать структурную схему и рассчитать передаточные функции для замкнутой и разомкнутой систем.

Вторая часть.

1. Для исследуемой системы автоматического управления определить переходную и импульсную функции, построить переходный процесс.

2. Выбрав по желанию любой критерий устойчивости линейных систем, сделать выводы по устойчивости изучаемой системы автоматического управления.

3. Построить частотные характеристики системы.

4. Проанализировать качество управления системы (определить прямые и косвенные оценки).

5. Построить логарифмические частотные характеристики системы управления, оценить запасы устойчивости.

Третья часть.

1. Ввести в исследуемую линейную систему автоматического управления нелинейный элемент, преобразовать полученную нелинейную систему.

2. Провести линеаризацию нелинейной системы.

3. Построить фазовый портрет.

4. Сравнить характеристики линейной и нелинейной систем автоматического управления.

ЧАСТЬ ПЕРВАЯ

Ввиду простоты и наглядности, автором данной работы была выбрана система автоматического управления станком шлифования валов.

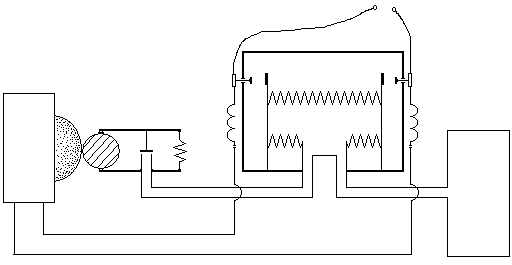
Рис.1. Принципиальная схема системы автоматического управления станком шлифования валов.

Принцип действия. На станок (1) подается непрерывный электросигнал из сети (2) через сильфонный прибор. Этим сигналом станок приводится в рабочее состояние и начинает шлифовать (стачивать) вал (3). По мере уменьшения диаметра шлифуемого вала, плавающие губки (4) сближаются, расстояние между соплом (5) и заслонкой (6) уменьшается. Уменьшение просвета «сопло-заслонка» приводит к увеличению давления в измерительной ветви (7), и, соответственно, в камере (8) сильфонного прибора, куда подается постоянное давление из специального устройства (9). Под действием нарастающего давления камера постепенно расширяется, и при определенном значении давления, происходит соприкосновение контактов (10) с клеммами (11). Это приводит к уменьшению тока в цепи «станок – сильфонный прибор», что, в свою очередь, вызывает размыкание индукционных реле (12). Поступление электрического сигнала к станку прекращается и станок выключается.

Объект регулирования (ОР) – шлифовальный станок, управление которым ведется с целью уменьшения диаметра вала.

Регулируемая величина X(t) – диаметр вала.

Управляющее воздействие Q(t) – подача электрического сигнала на станок.

Исполнительное устройство (ИУ) – сильфонный прибор, состоящий из камеры давлений (8), контактов (10), клемм (11). От сильфонного прибора зависит наличие или отсутствие электросигнала в цепи станка.

Датчик (D) – измерительная головка, состоящая из плавающих губок (4), сопла (5), заслонки (6), стягивающей пружины (13), измерительной ветви (7). Датчик служит для измерения регулируемой величины (диаметр вала) и преобразования ее в давление в камере.

Задающих устройств два:

ЗУ1 – источник электросигнала в сети.

ЗУ2 – устройство, подающее постоянное (заданное) давление в камеру. Рассмотрим, как в данной САУ происходит работа сравнивающего устройства. Выходной сигнал от задающего устройства – предписанное давление . Выходной сигнал от датчика – действительное значение давления , которое передается на сравнивающее устройство с помощью измерительной ветви. Работа сравнивающего устройства заключается в сравнении этих двух сигналов. В результате, чем больше давление в камере, тем больше она расширится, и тем скорее контакты соприкоснутся с клеммами, и тем скорее станок отключится. Величина изменения давления в камере сильфонного прибора определяется уравнением:

Исходя из принципа действия данной САУ нелинейный элемент НЭ (индукционное реле) расположен между сильфоном (ИУ) и станком (ОР).

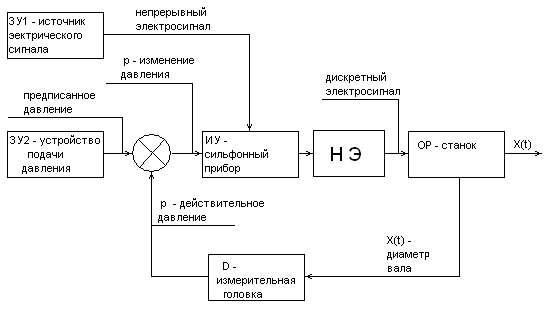
Рис.2. Полная функциональная схема исследуемой САУ.

При исследовании линейной части данной САУ и нахождения уравнения ее передаточной функции рационально воспользоваться абстракцией полной функциональной схемы. Для этого из полной схемы исключим задающие устройства (как внешние, постоянные по величине, не влияющие на динамику системы) и нелинейный элемент.

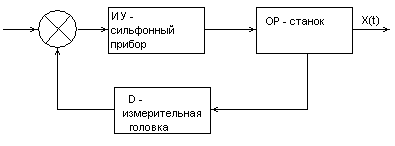
Рис.3. Абстрагированная функциональная схема.

Каждому звену в данной схеме соответствует определенная передаточная функция. Передаточная функция сильфона: - колебательное звено. Передаточная функция станка: - колебательное звено. Передаточная функция датчика: - реальное интегрирующее звено.

Т_сф – постоянная времени сильфона, Т_сф = 0,03с; k_сф – передаточный коэффициент сильфона, k_сф=0,4; - коэффициент демпфирования сильфона, ; Т_ст – постоянная времени станка, Т_ст = 0,00008с; k_ст – передаточный коэффициент станка, k_ст=1; - коэффициент демпфирования сильфона, ; Т_д – постоянная времени датчика, Т_д = 0,0002с; k_д – передаточный коэффициент датчика, k_д.=2.

Общая передаточная функция (для замкнутой системы):

Передаточная функция разомкнутой системы:

ЧАСТЬ ВТОРАЯ

Для определения устойчивости системы, запасов устойчивости, прямых и косвенных оценок необходимо рассчитать и построить ряд различных характеристик (переходная, импульсная функции, АФХ, АЧХ, ЛАЧХ, ЛФЧХ).

Для этого можно воспользоваться пакетом прикладных программ Mathsoft Apps (MathCad, MathLab)

Проверим систему на устойчивость, по критерию устойчивости Ляпунова.

Найдем полюса (корни хар-ского уравнения) передаточной функции :

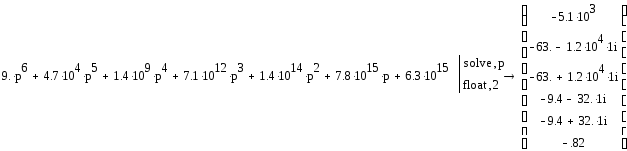
Все полюса имеют отрицательную вещественную часть, следовательно, система устойчива.

Построим переходный процесс и определим прямые оценки качества системы.

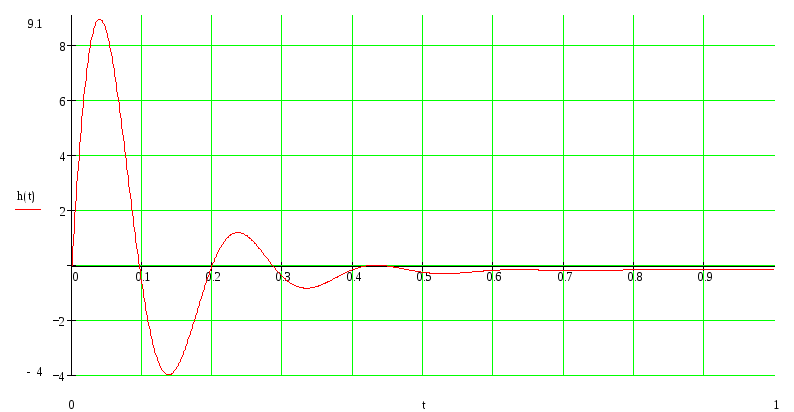
1. Время переходного процесса системы – это время регулирования системы, определяется как интервал времени от момента приложения какого-либо воздействия на систему до времени вхождения системы в 5% трубку. tn = 0,38

2. Перерегулирование (максимальная динамическая ошибка)

3. Колебательность – число колебаний системы от момента воздействия на нее до перехода в установившееся состояние. N=2

4. Время нарастания регулируемой величины – время, при котором выходная величина достигает своего максимального значения. tm=0,35с.

5. Время первого согласования – время, за которое регулируемая величина первый раз достигнет своего установившегося значения. t₁ = 0.95c.

Построим АЧХ и определим косвенные оценки качества системы.

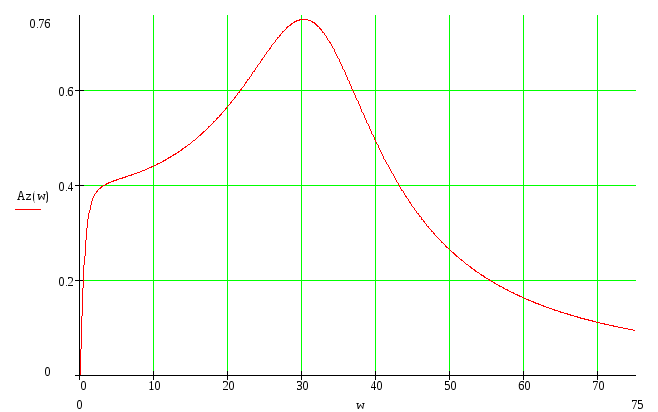
1. Показатель колебательности:

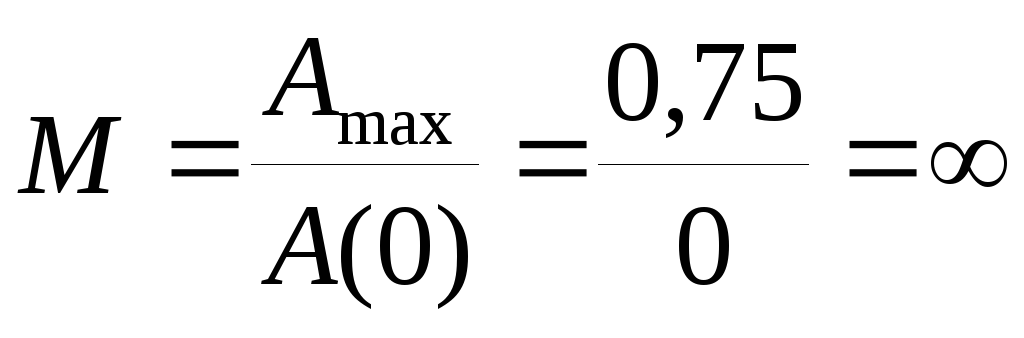
2. Резонансная частота – частота, при которой амплитуда достигает значения максимума: р=31

3. Частота среза определяется как частота, при которой АЧХ принимает значение 0,1: ср=73

4. Полоса пропускания частот – интервал частот, когда значения АЧХ больше, чем 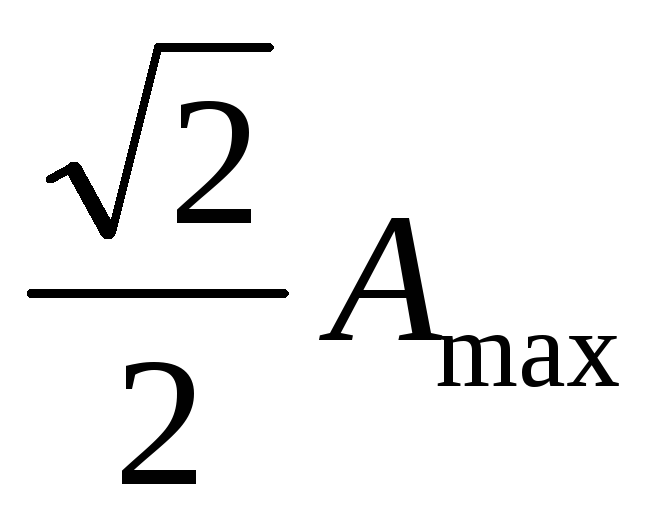(=0,53): (1, 2) = (18; 39)

Построим ЛАЧХ и ЛФЧХ и определим запасы устойчивости системы по амплитуде и по фазе.

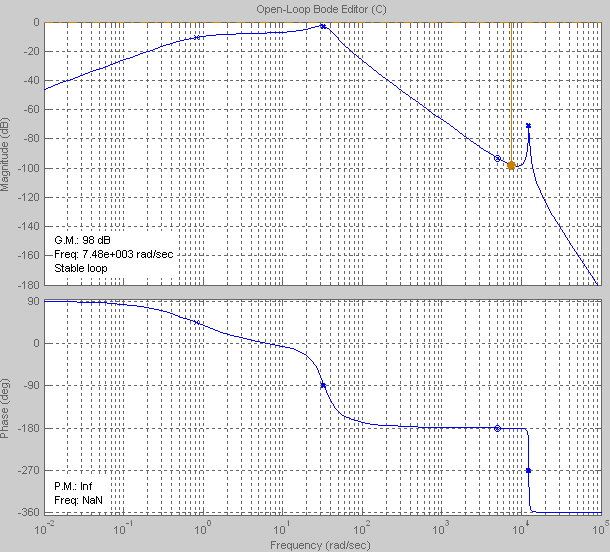
Запас по амплитуде составляет 98 децибел.

Запас по фазе бесконечен.

ВЫВОД. Анализ линейной части системы показывает, что при заданных параметрах система устойчива. Вследствие понижающего коэффициента усиления (K=0.8), данная САУ имеет большой запас устойчивости по амплитуде. Запас по фазе бесконечен.

При заданных параметрах качество работы системы близко к удовлетворительному. Система в целом работоспособна. Однако, слишком большие динамическая ошибка и время переходного процесса не позволяют использовать данную САУ в «ответственных» процессах, где к системе предъявляются повышенные требования.

Изменение качества работы системы достигается изменение ее параметров, либо введением в СУ дополнительных звеньев.

ЧАСТЬ ТРЕТЬЯ

Принцип работы рассмотренной САУ свидетельствует о том, что в системе имеется реле (см. рисунок 2) без зоны нечувствительности (идеальное реле).

При этом данная САУ может быть представлена функциональной схемой, приведенной ниже (Рисунок 5).

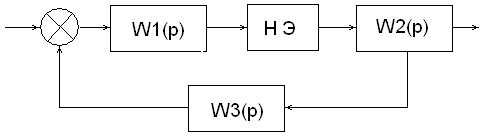
Рис.5. САУ с нелинейным элементом.

Характеристика идеального релейного выглядит следующим образом:

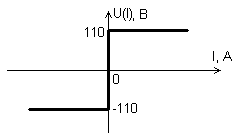
Для построения фазового портрета упростим структурную схему нелинейной СУ. Для этого выделим сгруппированные линейные элементы и нелинейный элемент.

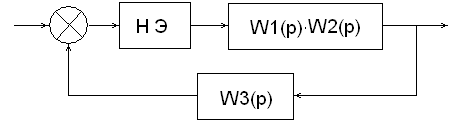
Разомкнем систему перед нелинейным элементом, перенося на новый вход системы регулирующее воздействие. Получим следующую структурную схему:

Окончательно получим:

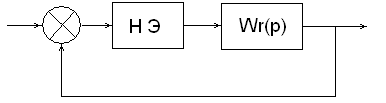
Передаточная функция линейной части соответствует передаточной функции САУ в разомкнутом состоянии.

Понижая порядок коэффициентов в числителе и, соответственно, в знаменателе, пренебрегая всеми значениями, для которых порядок множителя p меньше -2 , получим следующее выражение:

По определению передаточной функции:

Следовательно: p(0.018p+1)X=0.8X_i p(0.018p+1)X=0.8F(u-X)

Будем считать, что на вход системы подано постоянное воздействие , тогда перейдем от самих величин к их отклонениям относительно постоянного входного воздействия. Введем обозначения: ; ;

Получим дифференциальное уравнение фазовой траектории:

Решение данного уравнения будет строиться исходя из заданной нелинейности. Нелинейной частью системы является идеальное реле.

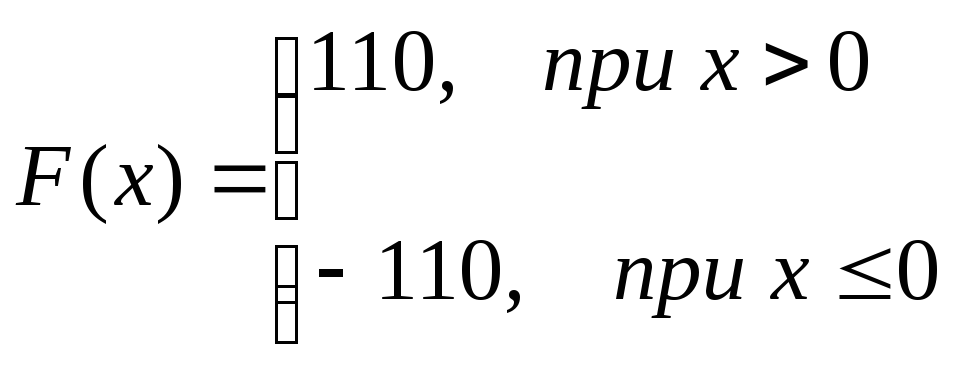
В соответствии с этим запишем дифференциальные уравнения для каждого участка:

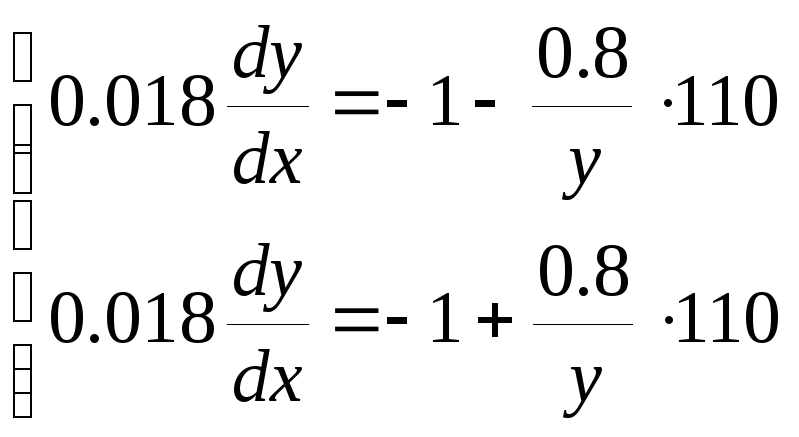
Пусть в начальный момент времени система выведена в точку М₀ с координатами (х_0, у₀). Проинтегрируем вышеприведенное выражение от х₀ до х и от у₀ до у.

Найдем решение каждого из уравнений системы по очереди:

1) .

Т.к. изначально система выведена в точку фазовой плоскости М₀ с координатами (x₀,y₀) , то интегрирование будет: от x₀ до x ; от y₀ до y.

Найдем решение каждого уравнения: 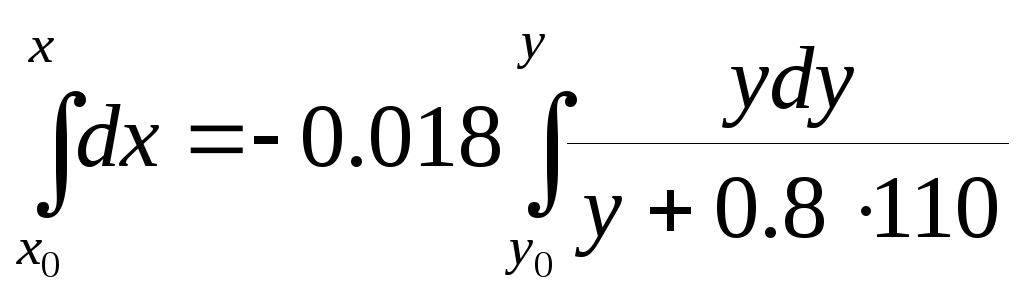получим:

2)

Задаваясь различными значениями "у" построим фазовый портрет системы. При этом выведем систему в произвольную точку (0.43; 0).

Первая кривая:

Вторая кривая:

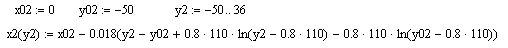
Третья кривая:

Четвертая кривая:

Пятая кривая:

Шестая кривая:

Седьмая кривая:

Восьмая кривая:

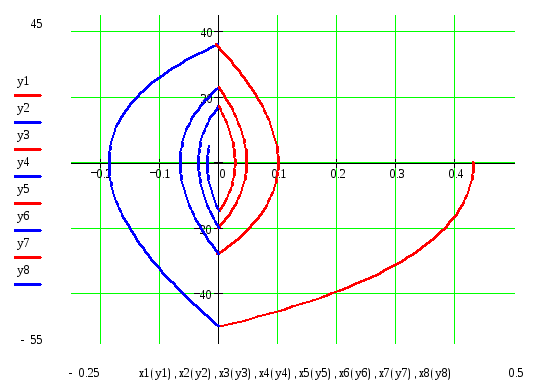
По полученному фазовому портрету проводим анализ устойчивости СУ. Фазовая траектория стремится к нулевому значению, что говорит об устойчивости системы. Вид фазовой траектории показывает, что качество управления оставляет желать лучшего. Улучшения качества можно добиться путем замены элементов системы, или изменением параметров уже имеющихся элементов.

P.S. Автор данной работы способен подробно разъяснить любые вопросы, возникшие при ее проверке.