Логістична модель

Розглянемо загальну картину динаміки тематичних інформаційних по-токів, обмежившись механізмами, типовими для новинного сегмента Інтернет.

Ми виходимо з того, що організації-генератори новинний інформації в абсолютній більшості працюють в стаціонарному режимі, який може характери-зуватися максимальною ємністю інформаційного простору N (зазначимо, що пи-тання про розмірності параметрів, а також про їх вимірі ми в даній роботі не роз-глядаємо).

Це означає, що кожна організація-генератор проводить потік інформа-ції, в середньому постійна за кількістю, як знаків, так і повідомлень. Змінюються в часі лише обсяги повідомлень, які відповідають тій або іншій темі. Іншими сло-вами, зростання кількості публікацій по одній темі супроводжуєтьсязменшенням публікацій на інші теми, так що для кожного проміжку часу T маємо:

де - кількість публікацій в одиницю часу, а M - загальна кількість усіх мо-жливих тем. Звичайно, передбачається, що частина завжди дорівнює нулю. Основний інтерес в такому формулюванні представляє вивчення динаміки окре-мого тематичного потоку, який описується щільністю .

Теоретично можна припустити, що безлічі публікацій, асоційованих з певним набором тим, перетинаються, тобто існують публікації, які можуть бути віднесені одночасно до декілька тем. Така "політематічность" дійсно є ефектом, з яким не можна не рахуватися, але в першому наближенні будемо вважати, що його внесок не спотворює загальну картину. Далі, будемо вважати, що протягом часу свого існування (актуальності) тема фіксує комплекс механізмів, які призво-дять до зростання кількості публікацій, що мають певні спільні риси. Різні темпи можуть породжувати різні за обсягом потоки публікацій, адже в цьому плані во-ни не є рівнозначними. Тому наформальному рівні зіставимо з темою як абстрак-тним поняттям два параметри: тривалість (характерне "час життя") і інтенсивність D. У рамках даної роботи будемо вважати інтенсивність величиною постій-ною. Це, звичайно, спрощений погляд, але цілком достатній для з'ясування загальних тенденцій.

Тривалість, як випливає зі сказаного вище, не обов'язково повинна спів-падати з початком і закінченням якоїсь події в реальному світі (або ряду подій). Вона характеризує лише характерний проміжок часу, протягом якого тема має закінчену актуальність. Інтенсивність можна визначити як величину, яка харак-теризує породжене відповідної темою кількість публікацій, усереднене по про-міжку .

Реакція медійних засобів, описувана величиною D, ніколи не буває мит-тєвою: завжди існує певна затримка в часі. Щоб врахувати цей аспект, введемо фактор запізнення Тепер можна запропонувати наступну якісну картину дина-міки тематичних інформаційних потоків. Генерація інформаційних потоків має дві основні складові: фонову та власне тематичну. Фонова складова визначається накладенням багатьох слабо пов'язаних між собою факторів та за певних умовах може наближатися (з точки зору тематичних розподілів) до шуму. Але вона за-безпечує публікацію більш-менш стабільного кількості матеріалів, відібраних за принципом "Треба ж щось публікувати! "

Виникнення нової теми викликає процес (точніше кажучи, комплекс процесів) перерозподілу мережевих ресурсів у зв'язку з появою актуальних сю-жетів. Обсяг фонових публікацій знижується, а тематичних - зростає. Якщо три-валості двох або більше тим перетинаються, то відповідні тематичні публікації також починають перерозподілятися між ними, причому характер перерозподілу визначається значеннями параметрів і D кожній теми. Коли ж тема втрачає ак-туальність, асоційовані з нею ресурси починають переходити чи в фонові пото-ки, або в інші тематичні.

Розглянемо саме тематичну складову, причому зосередимо увагу на ди-наміці потоків, породжених однією темою. Вивчення взаємодії кількох тем ста-новить окремий дослідження, яке виходить за межі поставленої нами задачі. На-ведемо приклади лише двох реальних інформаційних потоків, поведінка яких потрібно буде врахувати в моделі, яку опишемо нижче. У першому випадку (мал. 41 а) розглядалися публікації, які сканувалися системою моніторингу новин з Інтернет за тематикою хвороби та відходу від діяльності відомого політичного діяча. До моменту загострення хвороби обсяги публікацій щодо його діяльності були на досить високому рівні. Хвороба значно підвищила кількість публікацій, яка досягла верхнього рівня насичення.

Відомості щодо відходу від діяльності знизили кількість публікацій до нижньої планки, на цьому рівні і сталася остаточна стабілізація. Другий приклад- сенсаційне обрання мера великого міста (мал. 41 б). До виборчої кампанії про цю особу було не дуже багато публікацій в Інтернет, що відповідало нижній стабіль-ної планці. Вибори та затвердження мера супроводжувалися значною кількістю публікацій як позитивного, так і негативного характеру (верхня планка). Процес подальшої діяльності мера супроводжується обсягами публікацій, які відповіда-ють середньому стабілізаційному рівня.

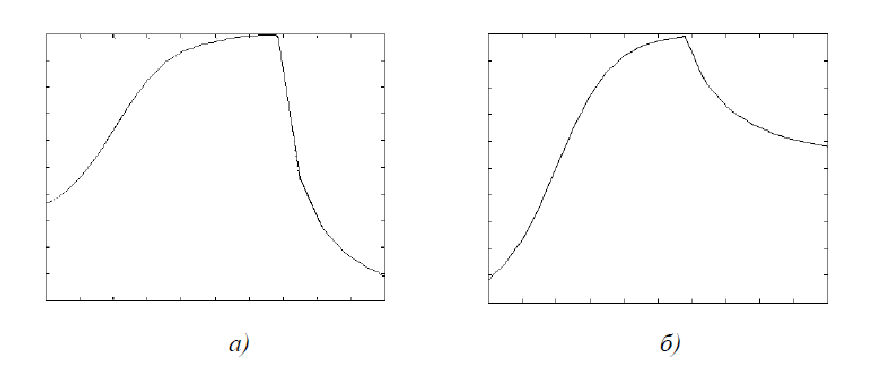Рис. 41. Приклади інформаційних потоків

При бажанні логістичну модель можна розглядати як узагальнення мо-делі Мальтуса, яка, як відомо, передбачає пропорційність швидкості росту функ-ції її значенню в кожний момент часу:

(3.9) де k - деякий коефіцієнт пропорційності. Оскільки розглядається динаміка окре-мого тематичного потоку, то далі не будемо писати для величин ni (t) індекси, які визначають тему.

Ідея полягає в тому, щоб зробити коефіцієнт у рівнянні Мальтуса функ-цією часу, причому так, щоб рішення не перевищувало заданого порогового зна-чення. Існують різні способи зробити це, але найбільш поширеним є викорис-тання константи, яка в явному вигляді обмежує зростання рішення. У нашому випадку з цією метою використовуємо ємність N. Тоді праву частину виразу (3.9) можна представити у вигляді:

де k - коефіцієнт Мальтуса, а r - фактор, який описує негативні для даної системи процеси, пов'язані з внутрішніми чинниками.

Тепер нам треба врахувати в явному вигляді параметри, які характеризу-ють вплив теми на динаміку публікацій. Оскільки інтенсивність D визначена на-ми як константа, її внесок представимо наступним чином:

Відповідно, будемо розглядати окремо дві тимчасові області: для яких рішеннями є функції u (t) і v (t). Повне рішення отрима-ємо шляхом "зшивки" на кордоні в точці :

Першою області відповідає процес зростання числа публікацій на дану тему в умовах її ненульовий актуальності (D> 0) і, можливо, перехід до стану насичення, а другий - процес скорочення числа публікацій, обумовлений втра-тою актуальності (D = 0). Отнорміровав параметри до порогової величиною N, представимо рівняння для першої області у такому вигляді:

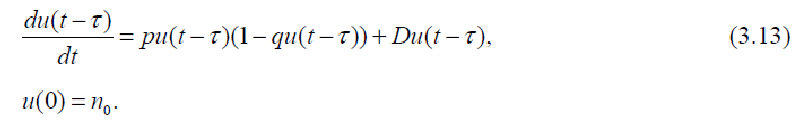Величина p визначає нормовану ймовірність в одиницю часу появи пуб-лікації незалежно від актуальності даної теми. Такий фактор відображає фонові механізми генерації інформації (Типовим прикладом може бути механічне пе-редрук матеріалів престижних інформаційних ресурсів). Величина D характе-ризує безпосередній вплив актуальність даної теми. Параметр q характеризує зменшення швидкості росту кількості публікацій і є величиною, зворотною аси-мптотичного значенню залежно u (t) при D = 0.

Початкова умова в (3.13) відображає два аспекти інформаційної дина-міки: по-перше, наявність фонової складової інформаційних потоків, а по-друге, невизначеність точного моменту, коли певна тема починає вносити свій внесок у загальний процес генерації публікацій. Зважаючи на це, в момент часу t = 0 існує деякий кількість публікацій, які можуть бути пов'язані з даною темою. Для дру-гої області, відповідно, маємо:

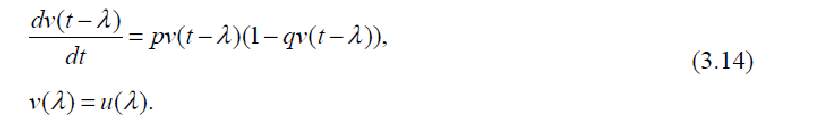
Так як у другій області тема вже не впливає на динаміку публікацій (во-на описує інерційні по відношенню до теми процеси), в рівнянні (3.13) не вклю-чається фактор запізнювання t. Граничне умова в (3.14) забезпечує "зшивання" функцій u (t) і v (t).

Рішення (3.13) має такий вигляд:

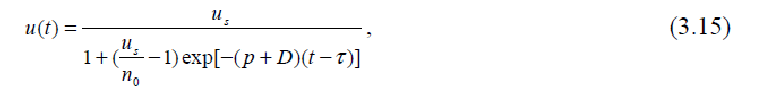
де - асимптотичну значення u, величина якого визначає область насичення (якщо, звичайно, дана залежність встигає її досягти):

Зауважимо, що вираз (3.16) не залежить від значення n0, що свідчить про неістотною для стану насичення інформаційної динаміки початкових умов. Яким би не було початкова кількість публікацій, насичення буде визначатися виключ-но параметрами, які характеризують фонову швидкість зростання числа публіка-цій, кількісну міру актуальності і негативні для процесу фактори. Тому з практ-ичної точки зору можемо знехтувати фоновими факторами, які погано піддають-ся вивчення.

Крива (3.15) має точку перегину:

Таким чином, для першої області маємо так звану S-подібну залежність, а при t ~ tinf залежність (3.15) наближається до лінійної і відповідає лінійної мо-делі. Уявімо тепер для зручності (3.15) в іншому вигляді:

З цього запису видно, що за умови

залежність u (t) має експонентний характер, причому її виразність визначаєтьсявеличиною запізнювання t. Отже, для значень t, значно менше ,наша модель збігається з експоненційної моделлю.

Типова залежність представлена на рис. 42.

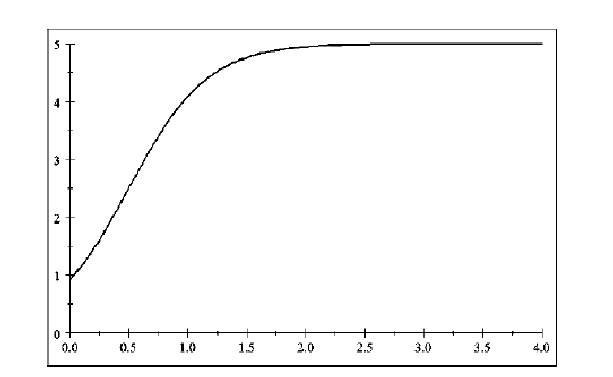Рис. 42. Область зростання

Перейдемо до другої області. Для неї рішення має такий вигляд:

Якщо залежність u (t) встигає досягти насичення за проміжок часу t <l, можемо спростити вирішення (3.20), представивши його наступним чином:

де vs = 1 / q асимптотичну значення залежно v (t). Як і слід було очікувати, вели-чина vs також не залежить ні від початкового умови, ні від умови "зшивання" на кордоні областей. У другій області динаміка публікацій у першому наближенні має експонентний характер, що збігається з результатами досліджень.

Типова залежність для другої області представлена на мал. 43.

Рис. 43. Область спаду

Отже, ми бачимо, що розглянута залежність має область насичення us (при ) і асимптотики vs, яка описує поступове зменшення кількості публік-ацій до фонового рівня. А це означає, що вона, принаймні якісно, узгоджена з загальними уявленнями про характері інформаційної динаміки, отриманими на основі експериментальних даних. Крім того, вона непогано співпадає з лінійною і експоненційної моделями на певних ділянках t.

Типова повна залежність n (t) наведена на рис. 44.

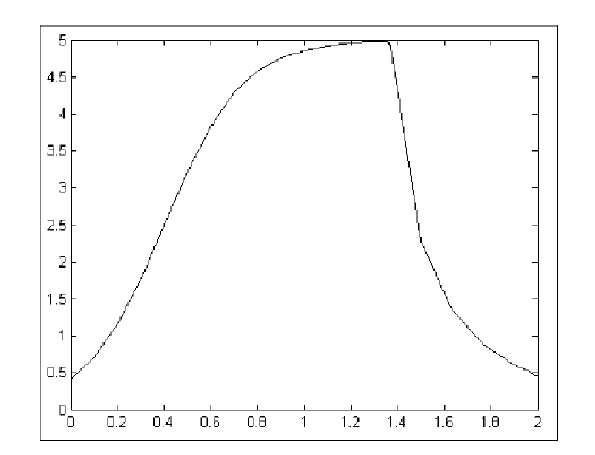Рис. 44. Узагальнений графік динаміки тематичного потоку

Отже, пропонована модель правильно описує (принаймні на рівні якіс-них властивостей) тимчасову залежність щільності публікацій, породжених окре-мою темою. Зокрема, вона містить область насичення, яку неможливо пояснити в рамках експоненційної моделі.

Ми також бачимо, що отримана залежність не є симетричною і має ха-рактерний "гребінець" на кордоні виділених двох областей. Рішення нашого рівняння для другої області, на відміну від першою, не має стану насичення: воно описує близьке до експоненціальним спад, який асимптотично наближа-ється до нуля. Така цікава особливість поведінки кривої насправді спостеріга-ється на практиці в певній частині випадків, але не у всіх.

Експериментальні дані свідчать про наявність ще двох типів залежнос-тей, які не обговорюються в даній роботі. Зазначимо лише, що була розглянута найпростіша реалізація моделі. Не виключено, що більш складні її модифікації дадуть змогу описати всі основні різновиди реальної динаміки. Окрему проблему інформаційної динаміки представляють циклічні процеси росту і зниження активності інформаційних ресурсів, не пов'язані з власне інформаційними чин-никами (Наприклад, періодичне зниження кількості публікацій у вихідні дні).

Відкритою залишається проблема визначення співвідношення рішень наведених логістичних рівнянь з умовою балансу тем. Однак є вагомі підстави для твердження, що логістична модель насправді описує динаміку певної ка-тегорії тематичних інформаційних потоків.