
- •Раздел I механика поступательного и вращательного движения тел
- •1. Кинематика
- •1.1. Основные понятия кинематики
- •1.2. Законы сложения скоростей и ускорений
- •Основы динамики.
- •2.1. Инерциальные системы отсчета. Первый закон Ньютона
- •2.2. Масса. Количество движения. Сила. Второй закон Ньютона. Третий закон Ньютона
- •2.3. Вращательное движение твердого тела.
- •2.4. Момент инерции
- •2.5. Кинетическая энергия движения твердого тела
- •2.6. Теорема Штейнера
- •2.7. Момент количества движения
- •2.9. Второй закон Ньютона для вращательного движения
- •2.10. Гироскоп. Скорость прецессии гироскопа
- •2.11. Закон сохранения массы. Закон сохранения количества движения. Реактивное движение
- •Реактивное движение. Уравнение Циолковского-Мещерского
- •2.12. Закон сохранения момента количества движения
- •2.13. Механическая работа и потенциальная энергия. Типы равновесия
- •2.14. Закон сохранения энергии
- •2.15. Применение законов сохранения. Упругое соударение шаров
- •2.17. Силы трения
- •2.18. Силы тяготения.
- •Ускорение свободного падения
- •Космические скорости
- •2.19. Силы инерции
- •3. Механические колебания и волны
- •3.1. Гармонические колебания
- •3.2. Потенциальная, кинетическая и полная энергии
- •3.3. Пружинный, математический, физический и крутильный маятники
- •3.4. Затухающие колебания
- •3.5. Вынужденные колебания
- •3.6. Параметрический резонанс
- •3.7. Сложение колебаний одинакового направления
- •3.8. Сложение колебаний
- •Негармонические периодические колебательные
- •3.10. Механические волны. Фазовая скорость волны
- •3.11. Фазовая и групповая скорости распространения волн. Дисперсия. Формула Рэлея.
- •3.12. Стоячая волна
- •3.13. Эффект Допплера
- •3.14. Акустические волны
- •Основы гидродинамики и аэродинамики
- •4.1. Уравнение неразрывности струи
- •4.2. Уравнение Бернулли
- •4.3. Течение вязкой жидкости
- •4.4. Сопротивление движению тел в жидкостях
- •4.5. Кинематическая вязкость. Число Рейнольдса
- •4.6. Аэродинамические силы
- •Раздел II молекулярНая физиКа и термодинамика
- •Основные макропараметры
- •1.1. Температура
- •1.2. Давление
- •2. Идеальный газ. Уравнение состояния идеального газа
- •3. Законы Бойля Мариотта, Гей Люссака, Шарля,
- •3.1. Закон Бойля Мариотта
- •3.2. Закон Гей Люссака
- •3.3. Закон Шарля
- •3.4. Закон Дальтона
- •Идеальный газ во внешнем силовом поле.
- •5. Распределение частиц по скоростям при тепловом равновесии. Распределения Максвелла
- •6. Работа при тепловых процессах
- •8. Теплоемкость
- •8.1. Теплоемкость при постоянном давлении и при постоянном объеме
- •8.2. Теплоемкость одноатомного газа
- •8.3. Теплоемкость двухатомного газа
- •8.4. Теплоемкость твердого тела.
- •9. Адиабатический процесс
- •10. Цикл Карно
- •11. Необратимость тепловых процессов
- •12. Второе начало термодинамики. Энтропия
- •Агрегатные состояния вещества. Уравнение Ван дер Ваальса. Фазовые переходы
- •14. Жидкости
- •14.1. Поверхностные явления
- •14.2. Капиллярные явления
- •14.3. Упругость пара над искривленной поверхностью
- •14.5. Кристаллические модификации
- •Фазовые переходы второго рода
- •15. Столкновения молекул и явления переноса
- •Диффузия, теплопроводность,
- •15.2. Средняя длина свободного пробега молекул, среднее время свободного пробега молекул, средняя частота столкновений молекул
- •15.3. Прицельный параметр и эффективное сечение столкновений
- •Коэффициент диффузии
- •15.5. Коэффициент теплопроводности
- •15.6. Теплосопротивление
- •15.7. Внутреннее трение в газах. Вязкость
- •15.8. Свойства газов при низких давлениях
- •Содержание
- •Раздел I. Механика поступательного и вращательного
- •Кинематика . . . . . . . . . . . . . . . . . . . . . . . . . 3
- •1.1. Основные понятия кинематики . . . . . . . . . . . 3
- •Раздел II. Молекулярная физика и термодинамика . . . . . 109
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3, тел. 952-04-41
3.7. Сложение колебаний одинакового направления
Этот случай часто реализуется в практической деятельности человека: вибро-машины, виброгасители, рессоры и т.д.
Рассмотрим тело, участвующее в двух однонаправленных колебаниях одновременно. Примером устройства, реализующего эту ситуацию, может быть пружинный маятник, точка подвеса которого подвешена к неподвижной опоре на пружине.
Пусть
![]() соответствует колебаниям тела относительно
точки подвеса, а
соответствует колебаниям тела относительно
точки подвеса, а
![]() - колебаниям точки подвеса относительно
неподвижной опоры. Суммарное смешение,
очевидно, будет равно:
- колебаниям точки подвеса относительно
неподвижной опоры. Суммарное смешение,
очевидно, будет равно:
![]() .
.
Рассмотрим два случая:
-
Пусть
 .
Тогда
.
Тогда
![]() ,
,
где
![]() ,
,
![]() .
.
Видим, что амплитуда результирующих колебаний зависит от разности начальных фаз.
Если
![]() ,
то:
,
то:
![]() ,
,
и
в случае
![]() ,
амплитуда колебаний увеличивается и
становится равной
,
амплитуда колебаний увеличивается и
становится равной
![]() .
.
Если
![]() ,
то амплитуда результирующих колебаний
становится равной нулю.
,
то амплитуда результирующих колебаний
становится равной нулю.
Итак, в зависимости от начальной разности фаз, колебания либо усиливаются, либо взаимно гасятся.
-
Пусть
 ,
а
,
а
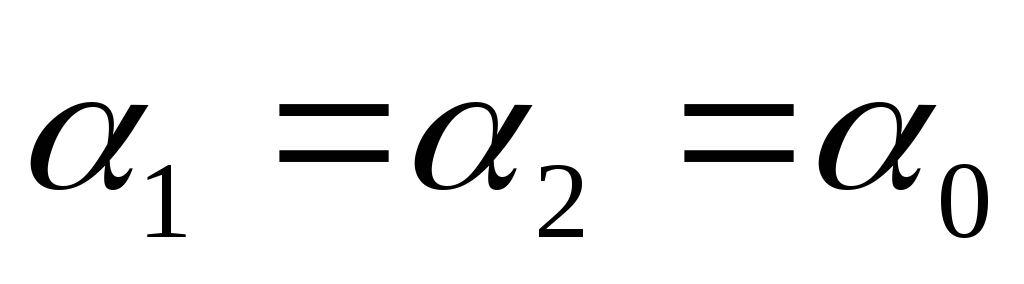 .
Тогда:
.
Тогда:
![]() ,
,
где
![]() .
.
Видим, что амплитуда колебаний зависит от времени, следовательно, эти колебания уже не являются гармоническими.
Если
![]() ,
то:
,
то:
![]() .
.
Итак, сложение однонаправленных колебаний разной частоты приводит к возникновению колебаний, амплитуда которых пульсирует во времени. Эти пульсации называются биениями.
3.8. Сложение колебаний
взаимно перпендикулярного направления
Пусть тело
одновременно совершает колебания вдоль
оси
![]() и вдоль оси
и вдоль оси
![]() с одной и той же частотой
с одной и той же частотой
![]()
![]() ,
,
![]() .
.
Найдем траекторию движения тела. Для этого изменим форму записи:
![]() ,
,
![]() ,
,
умножим
первое уравнение на
![]() ,
а второе на
,
а второе на
![]() и вычтем из первого уравнения второе:
и вычтем из первого уравнения второе:
 .
.
умножим
первое уравнение на
![]() ,
второе на
,
второе на
![]() и сложим уравнения:
и сложим уравнения:
 .
.
Далее, полученные выражения возведем в квадрат:


и почленно сложим.
![]() .
.
В результате проделанных действий получено уравнение, описывающее траекторию движения тела, одновременно участвующего в двух, взаимно-перпендикулярных колебаниях. Это уравнение эллипса.
Рассмотрим некоторые частные случаи.
1.
Если
![]() ,
то
,
то
![]() или
или
![]() .
.
Окончательно:
![]() - это уравнение прямой линии с углом
наклона к оси
- это уравнение прямой линии с углом
наклона к оси
![]() ,
равным:
,
равным:
![]() .
.
-
Если
 ,
то
,
то
 или
или

Окончательно:
![]() - это уравнение прямой линии с углом
наклона к оси
- это уравнение прямой линии с углом
наклона к оси
![]() ,
равным:
,
равным:
![]() .
.
-
Если начальные фазы отличаются на
 или
или
 ,
то
,
то
 - это уравнение эллипса, расположенного
симметрично относительно осей координат.
- это уравнение эллипса, расположенного
симметрично относительно осей координат.
Если
![]() ,
то траекторией движения является
окружность.
,
то траекторией движения является
окружность.
Верным
является также утверждение, что движение
по окружности всегда может быть
представлено в виде суммы взаимно
перпендикулярных гармонических колебаний
со сдвигом по фазе
![]() или
или
![]() .
.
Все прочие фазовые сдвиги дают эллипсы, не симметричные относительно осей координат (см. рис. 3.6).

Выше рассматривалось сложение взаимно перпендикулярных колебаний равных частот. Если частоты не равны, но кратны, то в результате сложения таких колебаний получаем, так называемые, фигуры Лиссажу (см. рис. 3.7).

