Глава II. «Элементы аналитической геометрии» § 1. Векторы. Сложение и вычитание векторов. Модуль вектора. Умножение вектора на число

Определение. Отрезок называется направленным (рис. 2.1), если указан порядок, в котором заданы концы отрезка.

Обозначение: . А В

Рис. 2.1

Определение. Длиной направленного отрезка называется длина отрезка АВ.

Обозначение:

Определение. Ненулевые отрезки и называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи АВ и СD.

Обозначение:  ().

Определение. Вектором называется множество всех одинаково направленных отрезков, имеющих равные длины. Каждый из этих направленных отрезков называется представителем вектора.

Определение. Два вектора и называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены какие-либо два представителя этих векторов.

Определение. Пусть заданы два вектора и . Направленный отрезок определяет вектор , который называется суммой векторов и .

= +

B

А С

Рис. 2.2

Правило треугольника: (рис. 2.2).

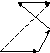
Откладывая векторы последовательно, можно найти сумму любого количества векторов, используя правило многоугольника (рис. 2.3).

D E

C

A B

Рис. 2.3

(рис. 2.3).

Для любых векторов :

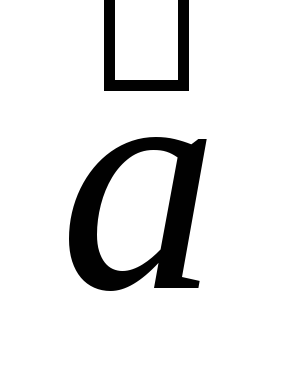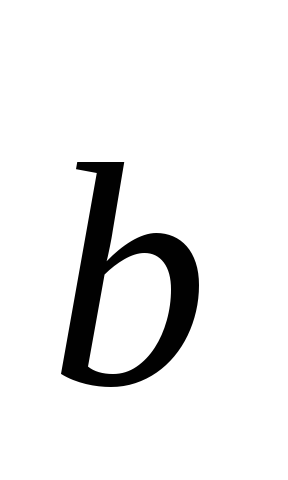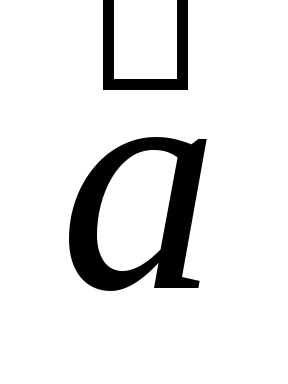1. += + — коммутативность сложения;

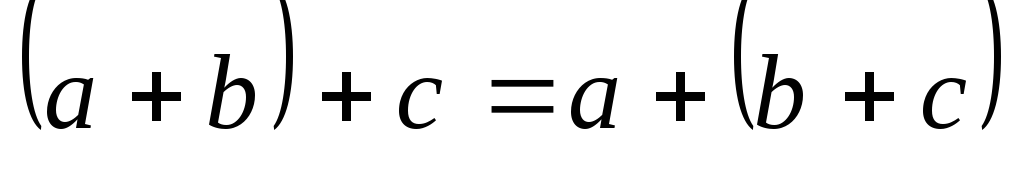2. — ассоциативность сложения.

Определение. Разностью векторов и называется такой вектор , что , .

Из треугольника ABC (рис. 2.4): .

B

А С

Рис. 2.4

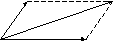
Правило параллелограмма: (рис. 2.5).

В С

А D

Рис. 2.5

Определение. Произведением вектора на действительное число  называется вектор , удовлетворяющий условиям:

1.; 2. , если   , , если   0.

Теорема. Для любых векторов и для любых действительных чисел  и  выполняются равенства:

1. ; 2. ;

3. ; 4. .

Определение. Векторы и называются коллинеарными, если существует прямая, которой они параллельны.

Теорема. Пусть . Векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т. е. .

Теорема. Пусть . Векторы и коллинеарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю, т. е. .

Определение. Коэффициенты разложения вектора по координатным векторам в прямоугольной системе координат называются координатами вектора .

Обозначение: .

Координаты вектора можно вычислить, зная координаты начала и конца этого вектора, т. е. если и , то .

Определение. Скалярным произведением двух векторов и называется произведение длин этих векторов на косинус угла между ними.

Обозначение: или , = .

Теорема. Длина вектора () в прямоугольной системе координат (О,) вычисляется по формуле .

Скалярное произведение = называется скалярным квадратом вектора , причем =. Таким образом, .

Теорема. Скалярное произведение векторов () и , заданных в прямоугольной системе координат (О,), выражается формулой =.

Условие перпендикулярности векторов и :

= 0, или в координатах: .

Косинус угла между ненулевыми векторами вычисляется по формуле:

сos (,)= или сos (,) = .