
Билет 6,15,24
Вывести интегральный признак Коши сходимости знакоположительного числового ряда. Исследовать на сходимость ряд Дирихле.
Интегральный признак Коши.
|
|
Пусть
при
Тогда
ряд
|
Доказательство.
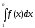 - это площадь под графиком функции
- это площадь под графиком функции
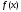 при
при
 .
.
Так
как
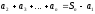 (сумма площадей прямоугольников)
ограничивает площадь под графиком
функции снизу, а
(сумма площадей прямоугольников)
ограничивает площадь под графиком
функции снизу, а
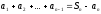 ограничивает ее сверху, то
ограничивает ее сверху, то
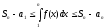 .
.
Пример.
Рассмотрим «ряды Дирихле»
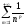 .
Название взято в кавычки, так неизвестно,
рассматривал ли эти ряды Дирихле, но
оно устоялось за долгие годы.
.
Название взято в кавычки, так неизвестно,
рассматривал ли эти ряды Дирихле, но
оно устоялось за долгие годы.
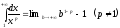 .
Ясно, что интеграл сходится при p>1
и расходится при P<1.
Случай p=1 рассмотрен выше
(расходящийся гармонический ряд). Отсюда
следует вывод
.
Ясно, что интеграл сходится при p>1
и расходится при P<1.
Случай p=1 рассмотрен выше
(расходящийся гармонический ряд). Отсюда
следует вывод
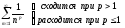 .
.
Интересно,
что ряд
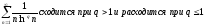 ,
интегралы
,
интегралы
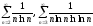 расходятся (проверьте по интегральному
признаку).
расходятся (проверьте по интегральному
признаку).
Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.
Билет 7, 16
Вывести признаки сравнения знакоположительных числовых рядов.
Первый признак сравнения рядов.
Пусть
выполнено неравенство
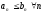 .
Тогда из сходимости ряда
.
Тогда из сходимости ряда
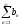 следует
сходимость ряда
следует
сходимость ряда
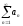 ,
а из расходимости ряда
,
а из расходимости ряда
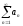 следует расходимость ряда
следует расходимость ряда
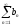 .
.
Замечание.
В силу свойства сходящихся рядов,
конечное число членов ряда не влияет
на сходимость и неравенство
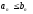 можно
проверять «начиная с некоторого n».
Поэтому эту фразу часто можно встретить
в теоремах о рядах. Иногда ее просто
опускают, но ее всегда надо иметь в виду.
можно
проверять «начиная с некоторого n».
Поэтому эту фразу часто можно встретить
в теоремах о рядах. Иногда ее просто
опускают, но ее всегда надо иметь в виду.
Доказательство.
1) Пусть ряд
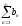 сходится.
Тогда выполнено неравенство
сходится.
Тогда выполнено неравенство
![]() .
Поэтому последовательность частичных
сумм
.
Поэтому последовательность частичных
сумм
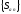 ограничена
сверху числом
ограничена
сверху числом
 .
Но эта последовательность не убывает.
Следовательно, по теореме Вейерштрасса
.
Но эта последовательность не убывает.
Следовательно, по теореме Вейерштрасса
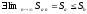 .
Последнее неравенство справедливо в
силу теоремы о предельном переходе в
неравенстве.
.
Последнее неравенство справедливо в
силу теоремы о предельном переходе в
неравенстве.
2)
Пусть ряд
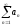 расходится.
Если ряд
расходится.
Если ряд
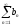 сходится,
то по п.1 доказательства и ряд
сходится,
то по п.1 доказательства и ряд
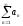 сходится.
Противоречие. Следовательно, ряд
сходится.
Противоречие. Следовательно, ряд
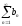 расходится.
расходится.
Пример.
Ряд
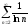 расходится, так как
расходится, так как
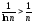 ,
а ряд
,
а ряд
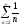 (гармонический) расходится.
(гармонический) расходится.
Второй признак сравнения.
Пусть
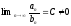 .
Тогда ряды
.
Тогда ряды
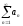 и
и
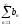 сходятся
или расходятся «одновременно», т.е. один
из них сходится, то и другой сходится,
если один расходится, то и другой
расходится.
сходятся
или расходятся «одновременно», т.е. один
из них сходится, то и другой сходится,
если один расходится, то и другой
расходится.
Доказательство.
Раскроем определение предела.
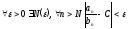 .
.
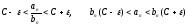 .
.
Если
ряд
 сходится,
то по 1 признаку сравнения ряд
сходится,
то по 1 признаку сравнения ряд
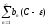 сходится (
сходится (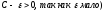 ,
ряд
,
ряд
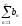 сходится
(свойство сходящихся рядов).
сходится
(свойство сходящихся рядов).
Если
ряд
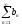 сходится,
то ряд
сходится,
то ряд
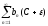 сходится (свойство сходящихся рядов),
тогда по 1 признаку сравнения ряд
сходится (свойство сходящихся рядов),
тогда по 1 признаку сравнения ряд
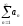 сходится.
сходится.
Пусть
ряд
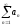 расходится.
Если ряд
расходится.
Если ряд
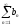 сходится,
то по предыдущему ряд
сходится,
то по предыдущему ряд
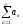 сходится
(противоречие).
сходится
(противоречие).
Пусть
ряд
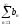 расходится. Если ряд
расходится. Если ряд
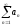 сходится,
то по предыдущему ряд
сходится,
то по предыдущему ряд
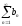 сходится
(противоречие).
сходится
(противоречие).


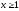 определена непрерывная, не возрастающая
функция f(x),
такая, что
определена непрерывная, не возрастающая
функция f(x),
такая, что
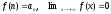 .
.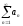 сходится
тогда и только тогда, когда сходится
несобственный интеграл
сходится
тогда и только тогда, когда сходится
несобственный интеграл
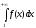 .
.