Цель работы: Знакомство с нелинейными САУ и методами их исследования с помощью фазовых траекторий и припасовывания.

ОСНОВНЫЕ СВЕДЕНИЯ

САУ называется нелинейной, если хотя бы одно звено системы описывается нелинейным уравнением (обладает нелинейной характеристикой). Если нелинейность играет в системе существенную роль, то она не подлежит линеаризации и для исследования САУ применяют теорию нелинейных систем. В нелинейных САУ различают статические и динамические нелинейности. Статические нелинейности – это нелинейности статических характеристик.

Рассмотрим нелинейное звено. Его статические характеристики могут иметь вид однозначных характеристик, представленных на рисунке 1 и неоднозначных представленные на рисунке 2.

а) непрерывная реальная б) непрерывная идеальная

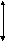
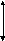
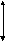
Зона нечувствительности

в) идеальная релейная г) релейная с зоной нечувствительности

Рисунок 1. Однозначные характеристики нелинейных элементов

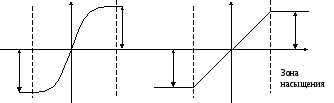
а) с насыщением и гистерезисом б) релейная с гистерезисом

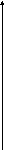
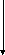
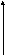
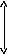
в) релейная с гистерезисом и зоной нечувствительности

Рисунок 2. Гистерезисные характеристики нелинейных элементов

Автономные системы не зависящие от времени пространства называют фазовым пространством, а траекторию изображающей точки фазовой траекторией.

Нелинейный элемент представляет собой чувствительный элемент со статической характеристикой в виде релейной характеристики с зоной нечувствительности рисунке 2 (г). Зададим параметры линейных элементов. Исполнительной устройство имеет передаточную функцию вида:

Передаточная функция объекта регулирования равны:

Заметим, что к=к₁к₂

Тогда линейная часть системы будет описываться уравнением:

Уравнение нелинейного элемента:

Запишем уравнение сравнивающего элемента:

Предположим, что задающее воздействие . Тогда уравнение нелинейной САУ будет иметь следующий вид:

Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них составляется линейное дифференциальное уравнение:

1 уч. , если у>b

2 уч. , если (1)

3 уч. , если у<-b

Для фазовой плоскости введем координаты у и . Исключим в уравнениях (1) время t.

Получим уравнения фазовой траектории для участков 1-3 нелинейной характеристики:

1 уч. ,если у>b

2 уч. , если

3 уч. , если у<b

ВЫПОЛНЕНИЕ РАБОТЫ

Зададим значения коэффициентов:

Зададим начальное значение для вектора у

Определим функцию D по 3-м линейным участкам нелинейной статической характеристики, задающую производную, приведя дифференциальное уравнение 2-го порядка к системе 2-х дифференциальных уравнений 1-го порядка.

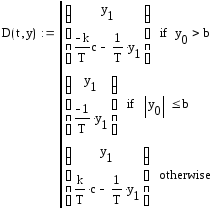
Найдем матрицу решения:

Построим траекторию на фазовой плоскости, предполагая, что первый столбец матрицы решения Y_i,0 содержит точки, в которых ищется решение дифференциального уравнения, второй Y_i,1 – содержит значения найденного решения, то есть y(t) и, наконец, третий столбец Y_i,2 содержит первые производные этого решения, то есть dy(t)/dt.

На рисунке 1 линиями переключения являются в=0,5 и в=-0,5

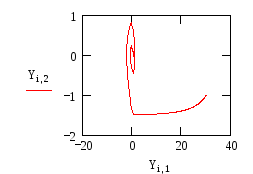
Рисунок 1. Фазовый портрет системы с нелинейным элементом

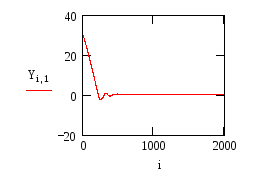
Рисунок 2. Переходной процесс системы с нелинейным элементом

ВЫВОД: Фазовая траектория образует устойчивый придельный цикл, который соответствует устойчивости системы

Автономные системы не зависящие от времени пространства называют фазовым пространством, а траекторию изображающей точки фазовой траекторией.

Метод фазовых траекторий основан на нахождении решения нелинейных ДУ в виде некоторой функции, графическое изображение которой на фазовой плоскости называется фазовой траекторией или фазовым портретом. Фазовая плоскость представляет собой плоскость на которой по двум координатам откладывается какие либо две переменные характеризующие динамику системы.

Устойчивые колебания описываемая на фазовой плоскости периодическим движением изображающей точки по некоторой замкнутой кривой. Такая кривая называется предельный цикл.

Сшивание фазовых траекторий на границе 2-х соседних листов называется припасовывание.

Метод припасовывания заключается в том, что нелинейная характористика заменяется несколькими линейными участками, а решение соответствующее этим участкам затем обобщаются.