
Задание 8.
Выбрать из диапазона устойчивости РС
конкретное значение и получить числовую
ПФ
![]() .
.
Выберем k=10. Для него
![]() (8.1)
(8.1)
Схема моделирования РС на ОУ приведена в Приложении 2.
Задание 9.
Получить оценки качества временных характеристик РС.
Разложив (8.1) на сомножители, получим
![]() .
.
Корни и полюсы полинома равны:
 (9.1)
(9.1)
Спектральные характеристики качества.
Степень устойчивости
 .
Для условий (9.1)
.
Для условий (9.1)
Степень быстродействия
 .
Для (9.1)
.
Для (9.1)
Степень жесткости

Степень колебательности

Время регулирования.

Перерегулирование

Затухание

Число колебаний в переходном процессе

Частотные характеристики качества.
Для определения частотных характеристик качества переходного процесса найдем ВЧХ P(w).


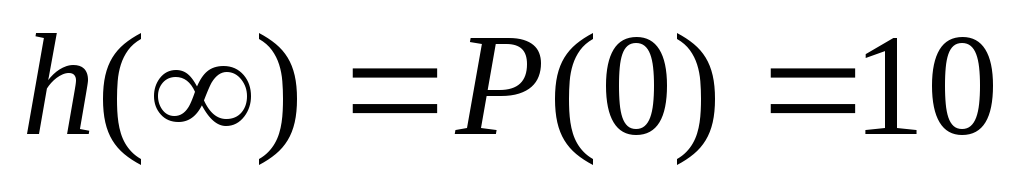
 при
при и
и
 получим, что
получим, что
так как P(w) – монотонная функция, то



Обобщая спектральные и частотные оценки, получим, что:
Задание 10.
Рассчитать частотными методами временные характеристики РС.
Воспользуемся корнями и полюсами ПФ, рассчитанными в (9.1).
Расчет импульсной характеристики.
Так как в ПФ есть действительный полюс и пара комплексно-сопряженных полюсов, то исходную ПФ можно расщепить на простые ПФ:
![]() (10.1)
(10.1)
Изображение (10.1) порождает оригинал
![]() :
:
![]() (10.2)
(10.2)
Найдем параметры (10.2)

Отсюда найдем окончательный вид (10.2):
![]()

Расчет переходной характеристики.
Изображение переходной характеристики
![]() РС имеет вид
РС имеет вид![]() .
Оригинал будет иметь вид:
.
Оригинал будет иметь вид:
![]() (10.3)
(10.3)
Найдем коэффициенты (10.3):

![]() из (10.2)
из (10.2)

Окончательный вид (10.3) следующий:
![]() .
.

Найдем показатели качества переходного процесса:
Точность регулирования

Время регулирования
 .
.
 при
при
Положительное перерегулирование

Отрицательное перерегулирование

Частота колебаний

Число колебаний
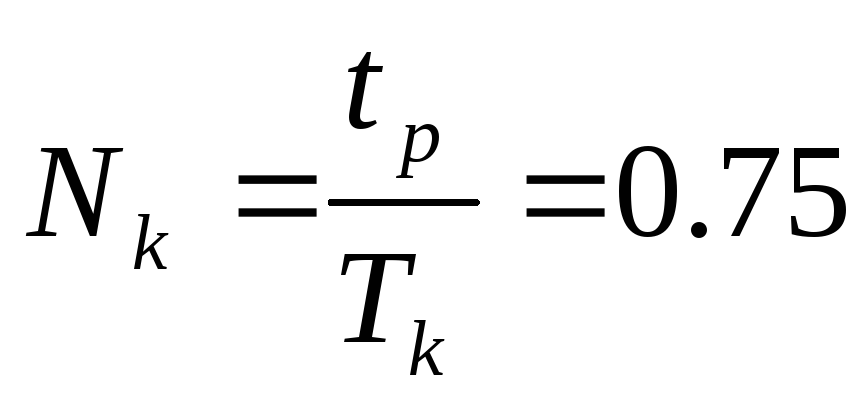
Затухание

Спектральные оценки переходного процесса дали правильные результаты для следующих параметров:
Время регулирования
Перерегулирование
Число колебаний
Затухание колебаний
Задание 11.
Рассчитать частотными методами реакцию РС на нетиповое входное воздействие.
Вид входного воздействия изображен ниже:

Аналитический вид входного воздействия
![]() .
Выходной сигнал будет иметь вид
.
Выходной сигнал будет иметь вид![]() ,
где первое слагаемое – свободное
движение, второе – вынужденное движение.
По условиям задания, начальные условия
в системе – нулевые, следовательно,
,
где первое слагаемое – свободное
движение, второе – вынужденное движение.
По условиям задания, начальные условия
в системе – нулевые, следовательно,![]() .
.
Найдем компоненты вынужденного движения:


где
![]() .
.
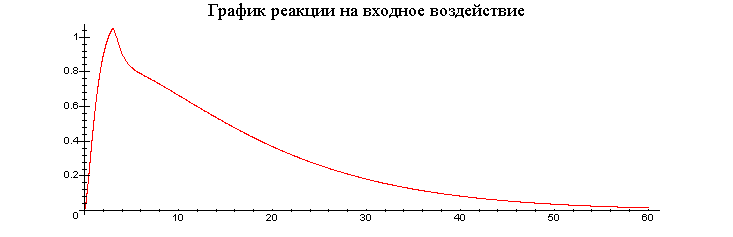
Реакция на входное воздействие
![]() .
.
График реакции на входное воздействие приведен ниже:
Задание 12.
Рассчитать частотными методами последовательный регулятор и построить схему моделирования ЗС с регулятором на ОУ.
При моделировании регулятора должны быть достигнуты следующие показатели качества переходного процесса:
Длительность переходного процесса =0.1 переходного процесса ЗС
Перерегулирование <30%
Запас устойчивости по амплитуде L>5дБ
Запас устойчивости по фазе >=300
Астатизм =0.1 астатизма РС.
Рассчитаем желаемый коэффициент усиления в низкочастотной части ЛАЧХ:
![]()
Определим частоты действия среднечастотной части ЛАЧХ и частоту среза по номограммам:

Схема последовательного регулятора
строится как
![]() .
Отсюда видно, что для упрощения регулятора
необходимо, чтобы в
.
Отсюда видно, что для упрощения регулятора
необходимо, чтобы в
![]() и
и
![]() были одинаковые звенья.
были одинаковые звенья.
Построим ЛАЧХж и ЛФЧХж:
График ЛАЧХ имеет следующие наклоны:
На частотах
 наклон составляет
наклон составляет .
.На частотах
 наклон составляет
наклон составляет
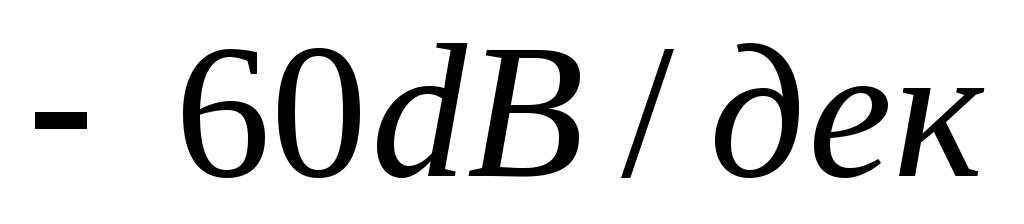 .
.На частотах
 наклон составляет
наклон составляет .
.На частотах
 наклон составляет
наклон составляет .
.На частотах
 наклон составляет
наклон составляет .
.

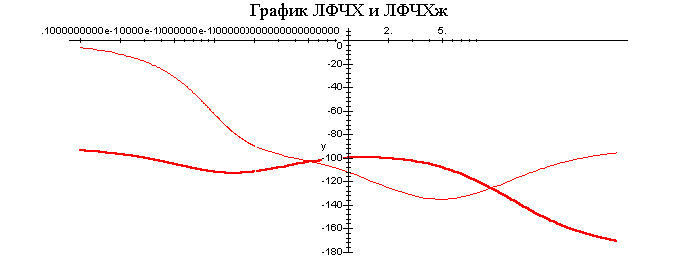
Исходя из этого, составим ПФ
![]() :
:
![]() .
.
ПФ регулятора составит следующий вид:

Проверим выполнение заданных условий по запасу устойчивости:
![]() при
при
![]() .
.
![]() при
при![]()
![]()
![]() условия
запаса устойчивости выполнены.
условия
запаса устойчивости выполнены.
Для проверки качества переходной функции
найдем
![]() .
.
![]()

Время регулирования

Перерегулирование
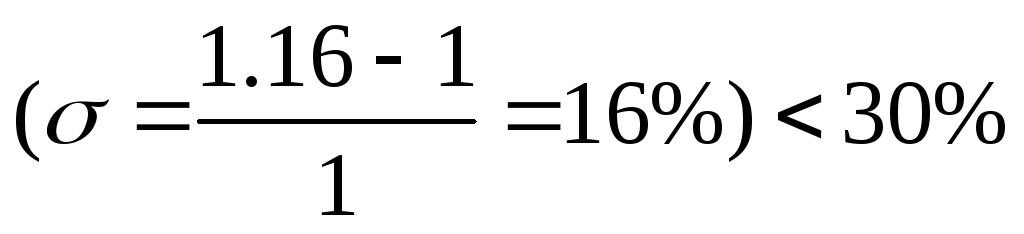 .
.
Следовательно, требования по качеству переходной характеристики также выполнены.
Схема моделирования ЗС с регулятором приведена в Приложении 3.
