Rozenbaum s., Brandro l.E.T. Brandгo, Rebello a., Fortunato g., (2008) Option value in presale of real estate property

Рассмотрим инвестора, который выкупаем единицу незавершенного строительства в момент времени t=0 по текущим ценам рынка. В условиях Бразильского рынка недвижимости этот инвестор заплатит 50% от полной стоимости недвижимости в течение периода застройки и оставшиеся 50% после завершения, и в тот же момент продаст эту недвижимость по ценам на рынке. Рыночная стоимость завершенного строительства неизвестна, и подвержена различным экономическим эффектам, таким как ставка процента, инфляция и других. Таким образом риск инвестора определяется как волатильность этой стоимости, и существует возможность, что в течение периода застройки, стоимость недвижимости упадет да такого уровня, что инвестору будет выгоде выйти из сделки путем отказа от договора купли-продажи и получить существенную часть вложенных денег обратно.

Авторы предположили, что цена на недвижимость подчиняется броумоновскому движению, описываемому с помощью уравнения:

,

где V-рыночная стоимость, dz-инкремент Винера, – ожидаемый рост стоимости недвижимости, - волатильность стоимости.

При расчетах авторами график выплат был взят, как 10% выплата в момент t=0, и далее 24 месячные выплаты по 1% плюс полугодовые платежи по 4%. На оставшиеся 50% суммы, начислялись проценты (15,73% годовых), что соответствует Бразильским процентам по кредитам в 2006 году.

Для того, чтобы оценить стоимость опциона на выход, авторы оценили волатильность в каждом регионе и получили значение, равное 10,13% в расчете на месяц. Для сравнительных целей авторы положили начальную стоимость (t=0), равной 100$. Эта стоимость относиться к концу 24 месяца, и приведенная стоимость всех выплат на начало периода (t=0) равны 87,21$.

Рассмотренные модели

Биноминальная:

, ,

Модель первого периода:

Начальное решение включает решение на покупку или не покупку недвижимости.

Если покупка – выплата 10% (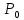), и теперь инвестор подвержен риску волатильности цен, которая увеличивается на фактор u с с вероятность p и уменьшается на фактор d с вероятностью 1-p и цена недвижимости – стохастический процесс со значениями между V1 = V0U и V1 = V0d.

Модель периодов 2 и 24

Далее решение 1, которое возникает в конце первого месяца и начале второго. Если выход – выплата процентов от внесенной суммы (δ) от выплат по возмещению (γ). В конце второго периода стоимость недвижимости - V2 ∈ {V0*u^2, V0*ud, V0*d^2}

Модель периода 24 и финального решения

В самом конце в финальном решении еще добавляется 50% стоимости недвижимости D.

Bulan l., Mayer c., Somerville c.T. (2009) Irreversible investment, real options and competition: Evidence from real estate development

Авторами были рассчитаны помесячные значения индекса повторных продаж для того, чтобы отследить изменение цен. При этом индексы были посчитаны раздельно по семи районам Ванкувера, при этом рассчитанные значения по трём районам из семи значительно отличаются друг от друга, в то время как остальные четыре имеют сходные значения. В качестве меры неопределенности была взята волатильность ежемесячных доходностей от вложений в строительство, рассчитанных по разным районам, при этом волатильность изменяется во времени и моделируется с помощью GARCH (1,1) процесса. Помимо данной меры вводятся еще два показателя неопределенности: дисперсия доходностей, рассчитанная по наблюдениям предыдущих двух лет, а также волатильность, скорректированная на ту долю волатильности, которая вызывается разницей в соотношении повторных продаж одного и того же объекта к общему объему сделок текущего месяца, и смоделированная с помощью процесса GARCH (1,1). Такие методы оценки неопределенности, как подчеркивает автор, согласуются с моделями реальных опционов, поскольку оценка с помощью GARCH-процессов представляет собой оценку ex ante, а девелоперы при принятии решения об исполнении опциона на строительство могут руководствоваться лишь такими оценками. Скорость неконтролируемого изменения цены рассчитывается с помощью авторегрессионного процесса, включающего лаги доходности вплоть до третьего порядка. Дивидендный доход выводится из комбинации ценовых индексов и данных опросов CMHC. Ставка дисконтирования рассчитывается как сумма скорости неконтролируемого изменения цены и дивидендного дохода. После этого измеряется мера систематического риска аналогично коэффициенту бета из модели САРМ: находится отношение ковариации избыточных доходностей и индекса TSE 300 и дисперсия TSE 300. При этом применялся метод локально взвешенной регрессии, разработанный Cleveland, Devlin (1988).

Модель отказов оценивалась с помощью метода максимального правдоподобия, при этом регрессия имела следующий общий вид:

где зависимая переменная h(t) – вероятность начала строительства в момент времени t, Х – вектор регрессоров, h₀(t) – базовая интенсивность отказов, отражающая трендовую составляющую (р – параметр Вейбулла):

При этом при рассмотрении всех спецификаций описанной выше регрессии авторы тестировали нулевую гипотезу β=0, что соответствовало коэффициенту 1 при регрессорах Х в модели отказов. Таким образом, полученные оценки коэффициентов сравниваются с 1, и дается заключение о том, что регрессор положительно влияет на вероятность начала строительства, если оценка коэффициента при нем больше 1, не влияет на вероятность начала строительства, если оценка коэффициента при нем равна 1, и негативно влияет на вероятность начала строительства в противном случае.

Общий список регрессоров Х:

• Семь переменных «реальная цена жилья», соответствующих семи районам Ванкувера

• Волатильность (дисперсия) доходности вложений в строительство, смоделированная с помощью GARCH-процесса

• Безрисковая ставка

• Скорость неконтролируемого изменения цены

• Скорость неконтролируемого повышения цены

• Скорость неконтролируемого понижения цены

• Систематический риск

• Специфичная для проекта ставка дисконтирования

В рамках базовой спецификации строились четыре регрессии, все из которых включали цены на жилье в семи районах Ванкувера и волатильность доходности. Спецификации отличались лишь способом расчета ставки дисконтирования:

• 1-ая регрессия: безрисковая ставка и скорость неконтролируемого изменения цены

• 2-ая регрессия: безрисковая ставка, скорость неконтролируемого изменения цены, систематический риск

• 3-я регрессия: специфическая для проекта ставка дисконтирования

При этом в регрессиях были получены знаки при коэффициентах основных регрессоров, в целом согласующиеся с моделями реальных опционов: цены в основном положительно влияют и значимы, при волатильности – коэффициент меньше единицы и значим (девелоперы предпочитают пережидать периоды с высокой волатильностью), безрисковая ставка значима и негативно влияет на вероятность принятия решения о реализации проекта (что согласуется с данными, полученными при опросе отраслевых менеджеров), в то время как скорость неконтролируемого изменения цены незначима. Вводя во второй спецификации модели систематический риск, авторы замечают, что он оказывается значимым и при этом делает более близким к единице идиосинкратический риск. Введенная в третьей спецификации специфическая для проекта ставка дисконтирования оказывается незначимой, поэтому в слующих регрессиях используется ставка дисконтирования из первой регрессии.

Стоит отметить, что незначимость скорости неконтролируемого изменения цены находится в соответствии с моделями реальных опционов, поскольку они предполагают независимость пороговой точки от скорости неконтролируемого изменения. Однако следует рассмотреть раздельное влияние скорости неконтролируемого повышения цены и скорости неконтролируемого снижения цены, что и делается в четвертой спецификации. При этом получается, что чем быстрее падают или растут цены, тем больше вероятность начать строительство в конкретный момент, что может быть объяснено стратегическим поведениям инвесторов.

Далее исследовалось влияние структуры рынка на решение девелопера исполнить опцион. При этом строились четыре регрессии, исследовавшие зависимость меры конкуренции (количество проектов) от следующих регрессоров:

• Семь переменных «реальная цена жилья», соответствующих семи районам Ванкувера

• Волатильность (дисперсия) доходности вложений в строительство, смоделированная с помощью GARCH-процесса

• Количество конкурентов

• Количество конкурентов*волатильность

• Безрисковая ставка

• Скорость неконтролируемого изменения цены

• Систематический риск

Построенные регрессии различались только радиусом, в котором брались проекты (1km, 2 km) и горизонтом (4 года, бесконечный период).

Результаты, полученные при оценке этих регрессий согласуются с гипотезой авторов о том, что конкуренция снижает стоимость опциона на ожидание. Об этом говорит значимость коэффициентов при волатильности, а также при переменной количество конкурентов*волатильность, при этом их влияние на зависимую переменную противоположно.

Результаты