2.2 Совершенные дизъюнктивная и конъюнктивная нормальные формы (сднф и скнф)
Сложность формулы (Y)=5*12=60
Сложность формулы (Y)=5*20=100
2.3 Анализ функции алгебры логики на принадлежность к классам
2.3.1 Анализ функции алгебры логики на принадлежность к классу функ кций сохраняющих ноль
Так как f(0, 0, 0, 0, 0) = 0, то данная функция алгебры логики принадлежит к классу функций сохраняющих ноль, т.е. fk0.
2.3.2 Анализ функции алгебры логики на принадлежность к классу функций сохраняющих единицу
Так как f(1, 1, 1, 1, 1)=0, то данная функция алгебры логики не принадлежит к классу функций сохраняющих единицу, т.е. fk1
2.3.3 Анализ функции алгебры логики на принадлежность к классу линейных функций
fл=CC0x0C1x1C2x2C3x3C4x4
Коэффициент С находим на наборе <0,0,0,0,0>
f(00000)= C00000=C=0,
тогда C=0
Коэффициент С4 находим на наборе <0,0,0,0,1>
f(00001)= 00 000C4*1=0,
тогда C4=0
Коэффициент С3 находим на наборе <0,0,0,1,0>
f(00010)= 0000C3*10=1,
тогда C3=1
Коэффициент С2 находим на наборе <0,0,1,0,0>
f(00100)= 000C2*100=0,
тогда C2=0
Коэффициент С1 находим на наборе <0,1,0,0,0>
f(01000)= 00C1*1000=0,
тогда C1=0
Коэффициент С0 находим на наборе <1,0,0,0,0>
f(10000)= 0C0*10000=1,
тогда C0=1
fл=01*x00*x10*x21*x30*x4=x3x0
В строке 3 идет несовпадение, значит функция не линейная, т.е. fkл.
2.3.4 Анализ функции алгебры логики на принадлежность к классу самодвойственных функций
=
;
функция несамодвойственна - не совпадает
с 1-ой строкой последнего столбца таблицы
истинности, значит данная функция
алгебры логики не принадлежит к классу
самодвойственных функций.
2.3.5 Анализ функции алгебры логики на принадлежность к классу монотонных функций
Проверим принадлежность функции алгебры логики к классу монотонных функций:
0<1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31
1<3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31
2<3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27, 30, 31
…
Так как 2>3, то f(2) >f(3), значит fkм функция не принадлежит к данному классу.
2.4 Минимизация функции алгебры логики
2.4.1 Минимизация с помощью карт Карно
Наносим функцию f(x0, x1, x2, x3, x4)=(2, 6, 10, 14, 16, 17, 20, 21,24, 25, 28, 29) на карту Карно
|
|
x4 |
|
||||||||||||
|
x0 |
|
x0 |
|
|
|
|||||||||
|
x1
|
25 |
29 |
13 |
9 |
24 |
28 |
12 |
8 |
||||||
|
27 |
31 |
15 |
11 |
26 |
30 |
14 |
10 |
x3 |
||||||
|
|
19 |
23 |
7 |
3 |
18 |
22 |
6 |
2 |
||||||
|
|
17 |
21 |
5 |
1 |
16 |
20 |
4 |
0 |
|
|||||
|
|
|
|
|
|
||||||||||
|
|
x2 |
|
x2 |
|
|
|||||||||
|
|
x4 |
|
||||||||||||
|
x0 |
|
x0 |
|
|
|
|||||||||
|
x1
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
x3 |
||||||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||||||
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|||||
|
|
|
|
|
|
||||||||||
|
|
x2 |
|
x2 |
|
|
|||||||||
Выполняем накрытие всех единичных значений функции алгебры логики: получаем 2 накрытия площадью 12 ячеек (обводим их).
Записываем МДНФ в виде логической суммы конъюнкций, соответствующих выполненным накрытиям:
f (x0,
x1,
x2,
x3,
x4)=
2.4.2 Минимизация методом Квайна - Мак-Класски
Запишем двоичные наборы, на которых функция f(x0,x1,x2,x3, x4)=(2, 6, 10, 14, 16, 17, 20, 21, 24, 25, 28, 29) равна единице:
00010, 00110, 01010, 01110, 10000, 10001, 10100, 10101, 11000, 11001, 11100, 11101.
Группируем наборы по числу единиц в наборах 5-ого ранга. Не склеенные наборы отмечаем знаком:
-
5-ый ранг
0 группа
1 группа
2 группа
3 группа
4 группа
5 группа
00010
10000
00110
01010
10001
10100
11000
01110
10101
11001
11100
11101
Выполняем функцию склеивания наборов из соседних групп.
Поскольку все наборы принимают участие в склеивании, то первичных импликант нет. В результате получаем наборы 4-ого ранга, которые также разбиваем на группы:
-
4-ый ранг
1 группа
2 группа
3 группа
00-01
0-001
-0001
1000-
100-0
10-00
0-110
01-10
10-01
1-001
1010-
1100-
11-00
1-101
11-01
1110-
Выполняя склеивание, переходим к наборам 3-его ранга:
|
3 ранг |
|
|
1 группа |
2 группа |
|
0--10 0--10 10-0- 1-00- 10-0- 1--00 1-00- 1--00
10- -0
|
1--01 1--01 1-10- 1-10- 11-0- 11-0-
|
|
|
|
|
|
|
|
|
|
|
3 ранг |
|
|
1 группа |
2 группа |
|
0--10 10-0- 1-00- 1--00
10- -0
|
1--01 1-10- 11-0- |
|
2 ранг |
|
1 группа |
|
1--0- 1--0- 1--0- |
|
2 ранг |
|
1 группа |
|
1--0- |
Мы получили 5 не склеиваемых набора,
внесем их в импликантную таблицу:
-
00010
00110
01010
01110
10000
10001
10100
10101
11000
11001
11100
10101
11101
01110
0-110
01-10
0
--10
1
--0-
Заполняем таблицу метками.
Вычеркиваем столбцы, имеющие только одну метку, и строки, дающие эти метки. Две строки вычеркнуты, значит, первичные импликанты 0--10 и 1--0- обязательно войдут в МДНФ.
Столбцы, имеющие хотя бы одну вычеркнутую метку, также вычеркиваем. В окончательном виде МДНФ имеет вид:
f (x0,
x1,
x2,
x3,
x4)=
2.5 Синтез схемы методом каскадов
Синтез логических схем можно производить в любом базисе, который обеспечен элементной базой, позволяющий реализовать все функции, входящие в базис. Основную роль при синтезе электронных схем играют функции логического умножения, сложения и отрицания ( И, ИЛИ, НЕ) и реализующие их логические элементы. Сложность синтезируемой схемы определяется сложностью формулы, описывающей конкретную логическую функцию.
МДНФ:
f (x0, x1, x2, x3,
x4)=
Рис. 2.3
Другой способ основан на использовании разложения Шеннона, которое дает возможность представить логическую функцию n переменных через функции (n-m) переменных, называемых остаточными функциями.
Размерность остаточных функций в свою очередь также можно понижать, исключая переменные из них, т.е. получая остаточные функции второго, третьего и т.д. порядка.
Один из методов, основанный на исключении переменной и получении остаточных функций, - метод каскадов. Этот метод базируется на понятии производной от функции алгебры логики.
Производная первого порядка
от ФАЛ по переменной Хi
равна сумме по модулю два нулевой и
единичной остаточных функций исходной
логической функции f:
.
Производная логической функции характеризуется весом который равен числу наборов на котором производная равна 1. Чем больше вес, тем в большей степени переменная оказывает влияние на функцию. Критерий оптимального исключения переменных состоит в том, что необходимо исключать переменные, производные по которым имеют наибольший вес.
Таким образом, при синтезе логических схем методом каскадов следует взять производные ФАЛ по всем переменным, определить вес каждой производной и исключать ту переменную, производная по которой имеет наибольший вес. После исключения переменной получают единичную и нулевую остаточные функции, к каждой из которых применяют тот же алгоритм.
Определяем производные функции алгебры логики по каждой из переменных:
- По переменной х0
- По переменной х3
- По переменной х4
Теперь определим вес каждой производной:
- По переменной х0
-
х0
х3
х4
(1)
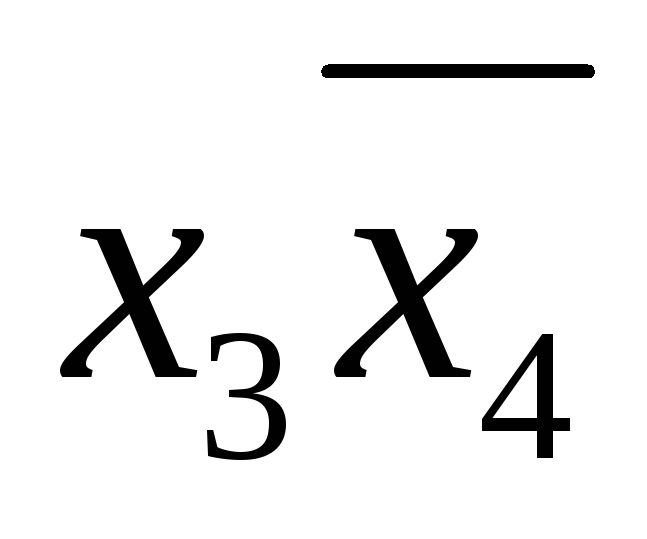
(2)
(1)(2)
0
0
0
0
1
1
0
0
1
0
1
1
0
1
0
1
0
1
0
1
1
0
0
0
1
0
0
0
1
1
1
0
1
0
1
1
1
1
0
1
0
1
1
1
1
0
0
0
Р0=6
- По переменной х3
-
(1) х0
х3
х4
(2)
(1)(2)
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
0
1
1
0
0
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
1
Р3=5
- По переменной х4
-
х0
х3
х4
(1)
(2)
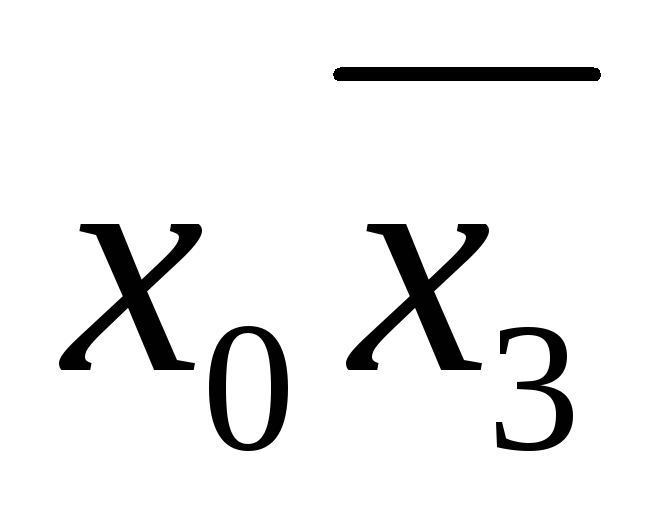
(1)(2)
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
1
0
1
0
1
1
1
0
1
1
0
0
1
1
0
1
0
1
1
1
0
1
1
0
0
0
0
1
1
1
0
0
0
Р4=2
Максимальный вес имеет производная ФАЛ
по переменной
,
следовательно, ее и исключаем из f(0).
После исключения можно записать нулевую
и единичную остаточные функции.
Полученные остаточные функции можно
реализовать при помощи двухвходовых
логических элементов и блоков исключения
переменной (см. рис.2.4).
Рис. 2.4