32

1. Задачи теории графов

Геометрический граф в пространстве ⁿ (Эвклидово пространство) – это множество V={v_i} точек пространства ⁿ и множество Е={e_k} простых кривых удовлетворяющих следующим условиям.

1)Каждая замкнутая прямая из множества Е содержит только одну точку v множества V;

2)Каждая незамкнутая прямая из множества Е содержит только 2 точки v из множества V, которые являются ее границами.

3)Кривые Е не имеют общих точек за исключением точек из множества V

Граф – это совокупность не пустого множества V, изолированного от него множества Е и отображения : ЕVV.

Если граф не имеет ребер, он называется вырожденным. Если множества Е и V конечные, то граф называется конечным.

1. Формализованное задание графа

Граф задается на множестве вершин V и множестве ребер Е. Наиболее простое описание графа – составление таблицы соответствия ребер и вершин.

Для удобства описания графа часто используют матрицы инциденций, смежности, циклов, разрезов и путей.

1.1.1 Описание графа с помощью таблицы

E	e1	e2	e3	e4	e5	e6	e7	e8	e9
V	v1, v2	v1, v3	v2, v3	v2, v4	v2, v5	v3, v5	v4, v5	v4, v6	v5, v6

1.1.2 Описание графа с помощью фактор – множества

1.1.3 Описание графа с помощью матрицы инциденций

Для графа G, имеющего n вершин и m ребер матрица инциденций имеет размерность n x m. Строки этой матрицы соответствуют вершинам, а столбцы – ребрам графа. Элемент а_ij=1, если j-ое ребро инцидентно i-ой вершине и а_ij=0 в противном случае.

Для графа на рис.1.1 матрица инциденций имеет вид:

1.1.4 Описание графа с помощью матрицы смежности вершин

Для графа G, имеющего n вершин матрица смежности вершин имеет размерность n x n. Элемент v_ij этой матрицы равен числу ребер, инцидентных одновременно i-ой и j-ой вершинам графа.

Для графа на рис.1.1 матрица смежности вершин имеет вид:

1.1.5 Описание графа с помощью матрицы циклов

Для графа G, имеющего n вершин и m ребер, матрица циклов имеет размерность к x m, где к – число циклов в графе. Элемент этой матрицы с_ij=1, если j-ое ребро входит в i-ый цикл и с_ij=0 в противном случае.

Рис. 1.2 – Изображение возможных циклов графа G

Для графа на рис.1.2 матрица циклов имеет вид:

1.1.6 Описание графа с помощью матрицы разрезов

Если задан связный граф G=(V, E) и множество его вершин разбито на два непустых подмножества W и W^/, то множество ребер, соединяющих W с W^/ называют разрезом. Простым называют разрез, разбивающий связный граф только на две компоненты связности. С использованием простых разрезов можно построить матрицу разрезов графа. Для графа G, имеющего n вершин и m ребер, матрица разрезов имеет размерность l x m, где l – число разрезов на графе. Элемент этой матрицы к_ij=1, если j-ое ребро входит в i-ый разрез и к_ij=0 в противном случае.

Для графа на рис.1.3 матрица разрезов имеет вид:

1.1.7 Описание графа с помощью матрицы путей

Выбрав в связном графе начальную (v₁) и конечную (v₂) вершину, для него можно составить матрицу путей (матрицу цепей). Строки этой матрицы соответствуют цепям между вершинами v₁ и v₂, а столбцы соответствуют ребрам графа. Элемент матрицы р_ij=1, если j-ое ребро принадлежит i-ой цепи и р_ij=0 в противном случае.

Для графа на рис.1.1 матрица путей имеет вид:

1.1 Числовые характеристики графа

1.2.1 Степени всех вершин графа

Число ребер неориентированного графа инцидентных вершине v, называется степенью вершины v и обозначается (v).

Степени всех вершин графа на рис.1.1:

(v₁)=2

(v₂)=4

(v₃)=3

(v₄)=3

(v₅)=4

(v₆)=2

1.2.2 Вершинная и реберная связность графа

Минимальное число вершин (ребер), удаление которых делает граф несвязным, называется вершинной (G) (реберной (G)) связностью графа G.

Вершинная и реберная связность графа на рис.1.1:

(G)=2

(G)=2

1.2.3 Цикломатическое число графа

Пусть G=(V, E) – неориентированный граф, имеющий n вершин, m ребер и r компонент связности. Цикломатическим числом графа G называют число (G)=m – n + r. Цикломатическое число равно наибольшему числу независимых циклов в графе.

Цикломатическое число графа на рис.1.1:

(G)=9 – 6 + 1 = 4

1.2.4 Вершинное и реберное числа независимости

Множество SV графа G = (V, Г) называют внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для любого хS имеет место ГхS.

Множество внутренней устойчивости, содержащее наибольшее число элементов, называют наибольшим внутренне устойчивым множеством, а число элементов этого множества – числом внутренней устойчивости ₀(G) графа G (это число называют также вершинным числом независимости графа).

Два ребра графа называют смежными, если они инцидентны одной и той же вершине. Максимальное число попарно несмежных ребер графа называется его реберным числом независимости ₁(G).

Вершинное и реберное числа независимости графа на рис.1.1:

₀(G)=2

₁(G)=3

1.2.5 Числа вершинного и реберного покрытий графа

Если ребро графа инцидентно его вершине, то говорят, что они покрывают друг друга. Множество вершин, покрывающих все ребра графа, называют вершинным покрытием графа G, а минимальную мощность этого множества - числом вершинного покрытия графа ₀(G). Аналогично, множество ребер, покрывающих все вершины графа, называют реберным покрытием графа G, а минимальную мощность этого множества – числом реберного покрытия графа ₁(G).

Числа вершинного и реберного покрытий графа на рис.1.1:

₀(G)=4

₁(G)=3

1.2.6 Вершинное и реберное число внешней устойчивости графа

Множество ТV графа G=(V, Г) называют внешне устойчивым, если любая вершина, не принадлежащая Т, соединена ребрами с вершинами из Т, т.е. для любого хТ имеет место ГхТ.

Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшим внешне устойчивым множеством, а число элементов этого множества – вершинным числом внешней устойчивости ₀(G) графа G.

Минимальная мощность множества ребер, покрывающих все ребра графа, называется реберным числом внешней устойчивости ₁(G) графа G.

Вершинное и реберное числа внешней устойчивости графа на рис.1.1:

₀(G)=2

₁(G)=2

1.2.7 Радиус и диаметр графа

Для фиксированной вершины v целое число R(v)=max d(v, w), wV соответствует расстоянию от v до наиболее удаленной вершины.

Радиус R₀= min R(v)= R(v₀), vV, вершину v₀ считают центром графа.

Диаметром связного графа называется максимальное расстояние между парами вершин.

Найдем радиус для графа на рис.1.4, считая v₂ – центром графа:

R₀=6

Найдем диаметр графа на рис.1.4:

(между парами вершин v₁ и v₆)

T=15

1.3 Задача коммивояжера

Постановка задачи: коммивояжер должен посетить по одному разу каж дый из n городов (каждая пара городов связана с дорогой) и вернуться в исходный город. При этом он должен выбрать кратчайший маршрут.

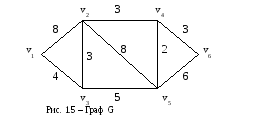
Решение:

Вершина V₁ обладает минимальной степенью  = 2, следовательно, числовозможных подграфов (G_i) для нахождения гамильтоновых циклов С²₂=1. Он имеет вид такой же, как и заданный граф.

Рассмотрим подграф G₁. Жирные ребра соответствуют ребрам искомого гамильтонова цикла. В скобках у вершины отмечаем число ребер оставшихся для исследования.

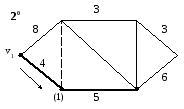
Длина цикла С₆=4+5+6+3+3+8=29

Рассмотрим альтернативу:

Вершина V₂ повторяется, значит, эта цепь не является частью гамильтонова цикла и отбрасывается. Дальнейшие построения не эффективны.

То есть кратчайшим гамильтоновым циклом графа G является цикл длинной 29.