курсовая работа / tau-zibben-auf / r-TAU-kursovik-var-83 / Курсов

Нижегородский Государственный

Технический Университет

ДИСЦИПЛИНА:

«Основы теории управления»

Курсовой проект

Выполнил:

Белоусова Е.А.

ФИСТ 99-В-3

Проверил:

Никулин Е.А.

Нижний Новгород

2002

Вариант 83

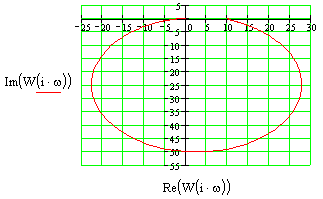
Структурная схема устройства

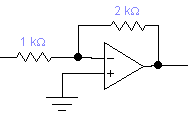
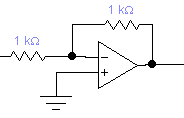
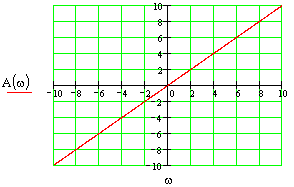
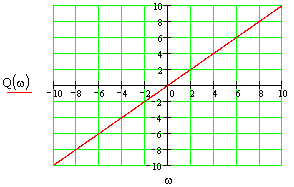
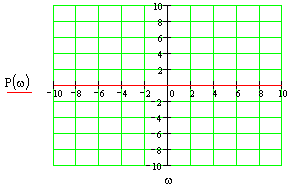
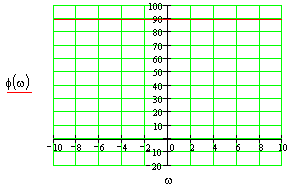
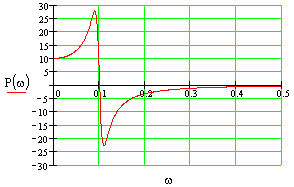
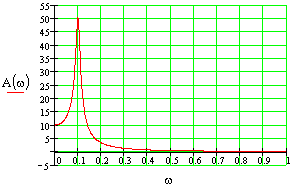
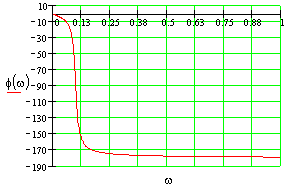
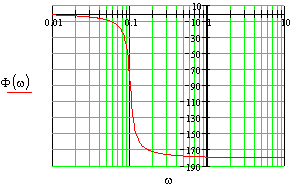
1. Построить все частотные характеристики блоков структурной схемы и принципиальные схемы моделирования блоков на операционных усилителях.

Первый блок.

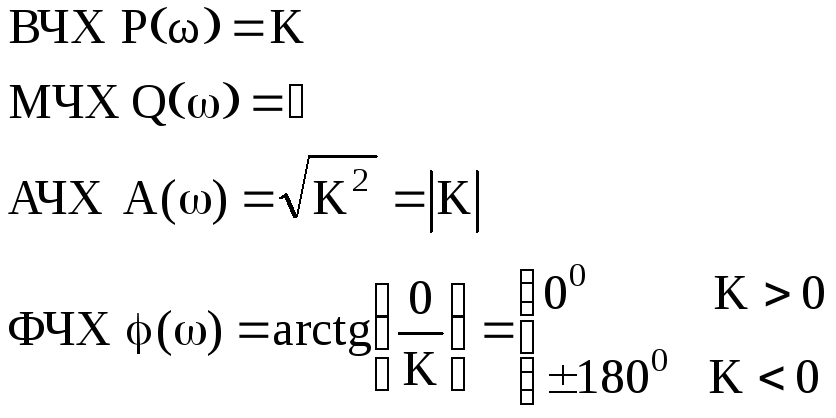
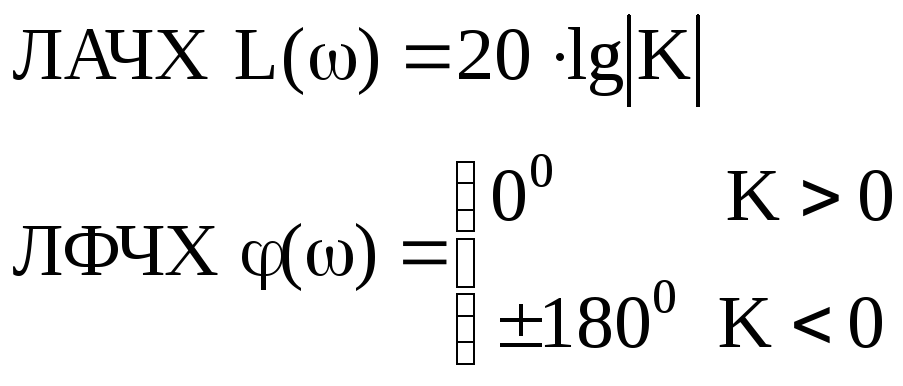
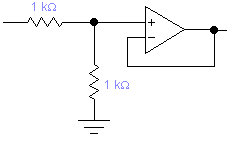
Это блок с буквенным параметром в передаточной функции, строим ЧХ для значений параметра: K={0.5;-2;-1}

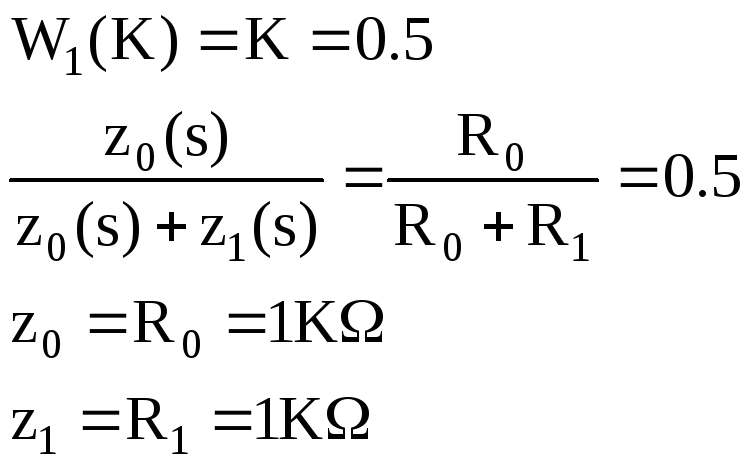
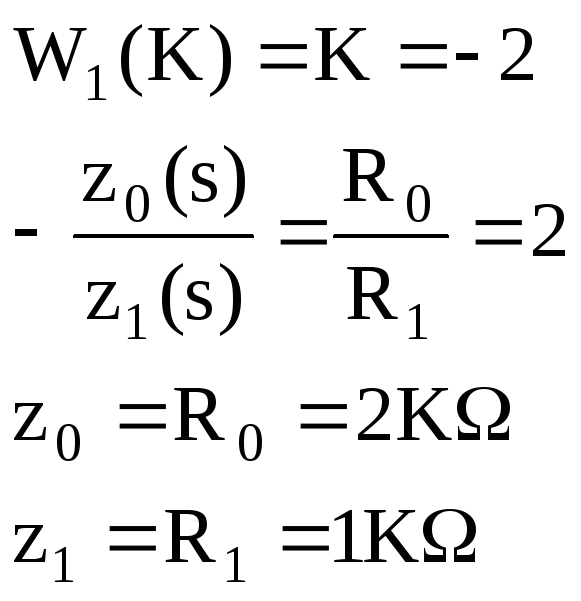
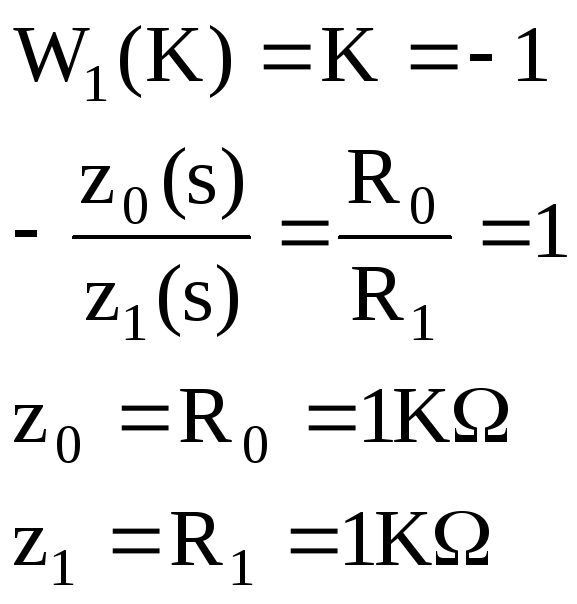
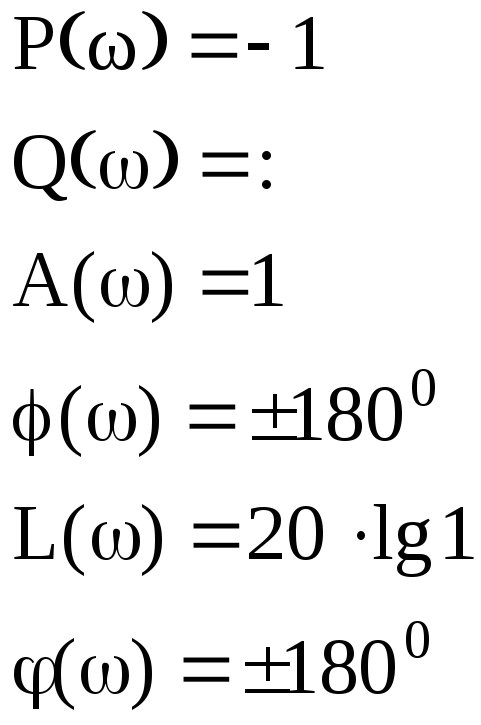
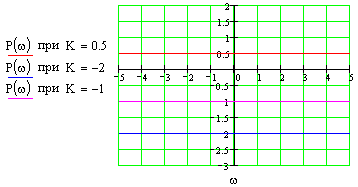
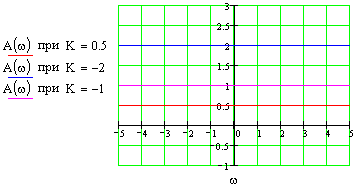
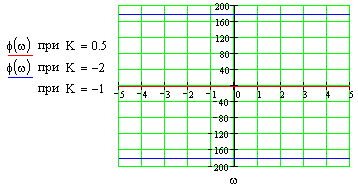
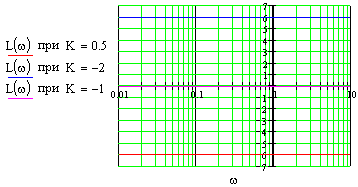
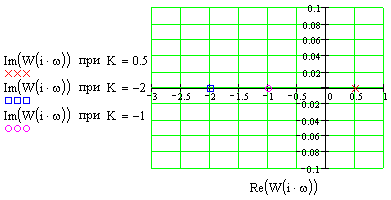
В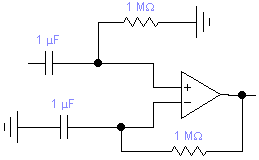торой блок.

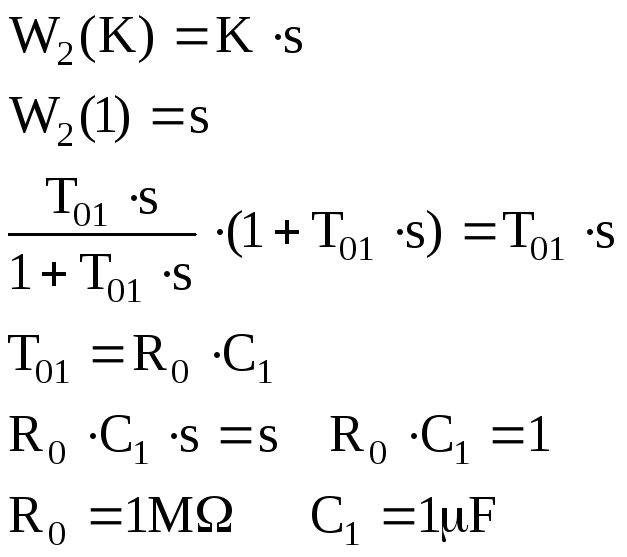
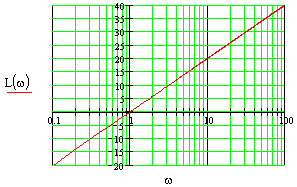
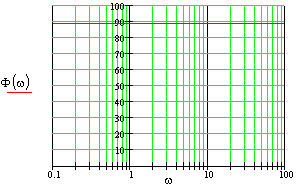
Т 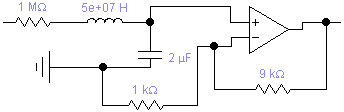ретий блок

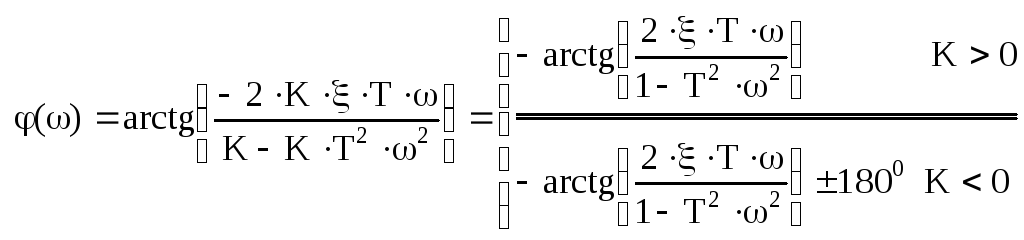
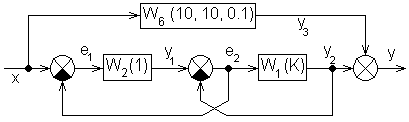
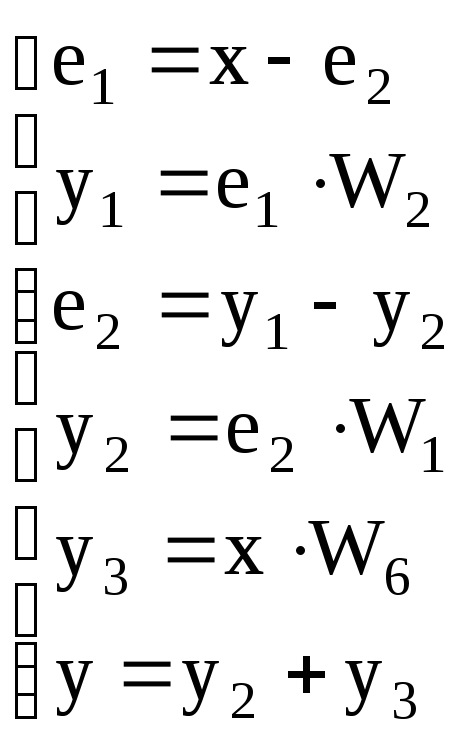
2. П олучить ПФ W_p(s) разомкнутой системы.

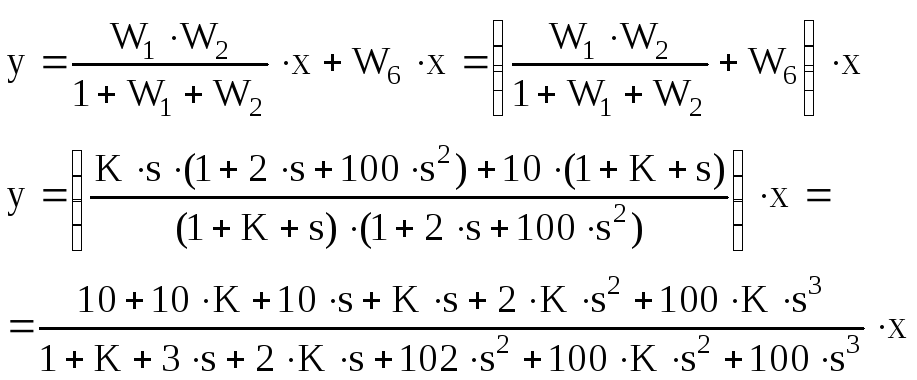
3. Исследовать устойчивость разомкнутой системы от буквенного параметра методами Гурвица и Михайлова.

Критерий устойчивости Гурвица.

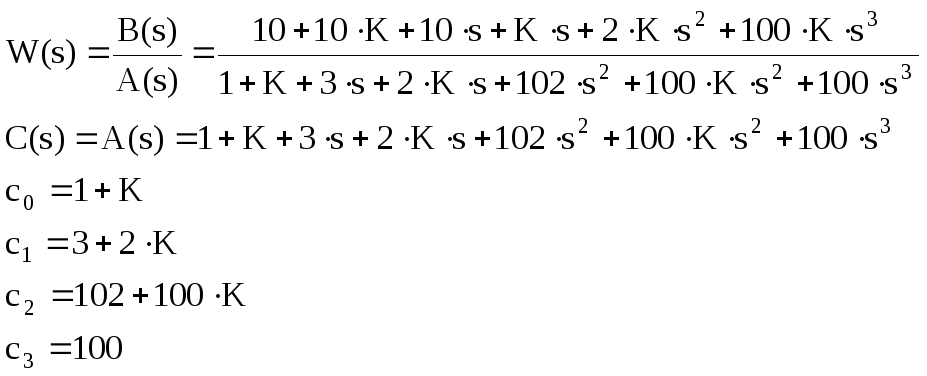
Для характеристического полинома третьей степени C(s)=c₀+c₁s+c₂s²+c₃s³ спектральное необходимое и достаточное условие устойчивости (НуДУУ) выглядит следующим образом:

{(sgn c₃)c₂>0}∩{M₂>0}∩{(sgn c₃)³M₂c₀>0}, то есть c₀, c₂, c₃ должны быть одного знака и M₂=c₂c₁-c₂c₀>0.

Так как c₃>0, то получаем следующую систему уравнений:

Уравнение не имеет действительных корней, так как коэффициент при K²>0, то неравенство выполняется при любых значениях K.

Разомкнутая система устойчива при K > -1.

Частотный критерий устойчивости Михайлова.

Д ля устойчивости линейной системы необходимо и достаточно, чтобы коэффициенты c₀ и c₁ ее ХП C(s) были ненулевыми и одного знака, а корни ω_i уравнений Re{C(jω)}=0 и Im{C(jω)}=0 чередовались по возрастанию в соответствии с 0=ω₀²< ω₁²( p )<…< ω_n-1²( p ).

Для ХП третьей степени {ω₁²=c₀/c₂>0}∩{c₀/c₂< ω₂²= c₁/c₃}∩{c₀c₁>0}, то есть пары к оэффициентов {c₀, c₁}, {c₀, c₂}, {c₂, c₃} должны быть одного знака и c₁c₂>c₀c₃.

4. П 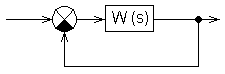олучить ПФ W₃(s) системы, замкнутой единичной отрицательной обратной связью.

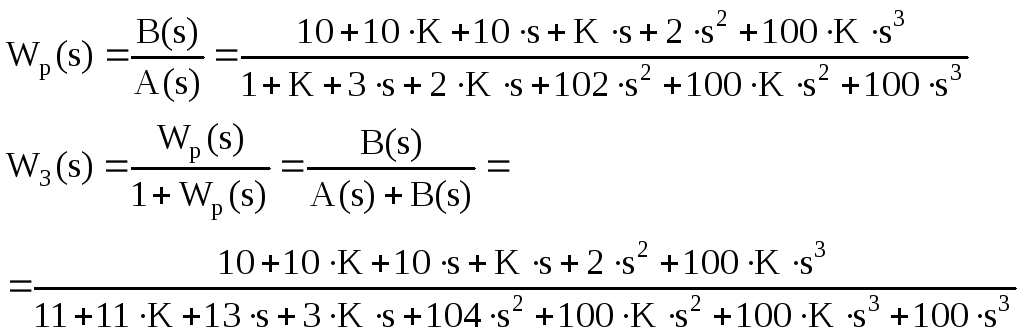
5. Исследовать устойчивость замкнутой системы от буквенного параметра методами Гурвица и Рауса. Получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.

C(s)=A(s)=11+11K+13s+3Ks+104s²+100Ks²+100Ks³+100s³

К ритерий устойчивости Гурвица.

Критерий устойчивости Рауса.

Критерием устойчивости действительного полинома является постоянство знаков всех элементов первого столбца таблицы Рауса.

П остроим таблицу Рауса.

6. Сформировать набор значений параметра, включающий все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости замкнутой системы.

	1	2	3	4	5
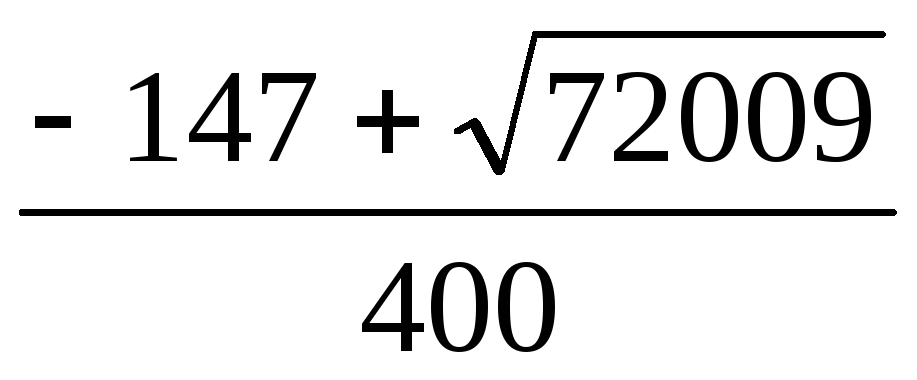
K	-1		-0.5	-2	0.5

Построим для них годографы для пункта 3:

K = -1 K = 0.3

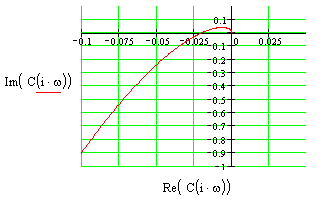
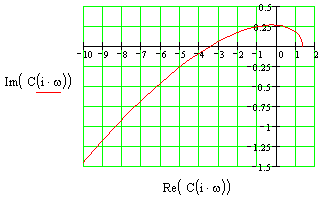
K = -0.5 K = -2

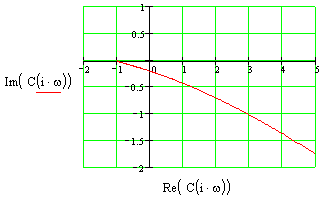
K=0.5

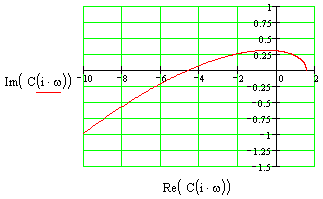
7. Для каждого значения параметра из набора построить частотные характеристики, необходимые для исследования устойчивости замкнутой системы от параметра по критериям Найквиста и Михайлова.

Частотный критерий устойчивости Михайлова.

Для устойчивости линейной системы необходимо и достаточно, чтобы коэффициенты c₀ и c₁ ее ХП C(s) были ненулевыми и одного знака, а корни ω_i уравнений Re{C(jω)}=0 и Im{C(jω)}=0 чередовались по возрастанию в соответствии с 0=ω₀²< ω₁²( p )<…< ω_n-1²( p ) или изменение аргумента годографа ее ХП степени n было определенным и составляло рад или n квадрантов при изменении частоты от 0 до ∞.

K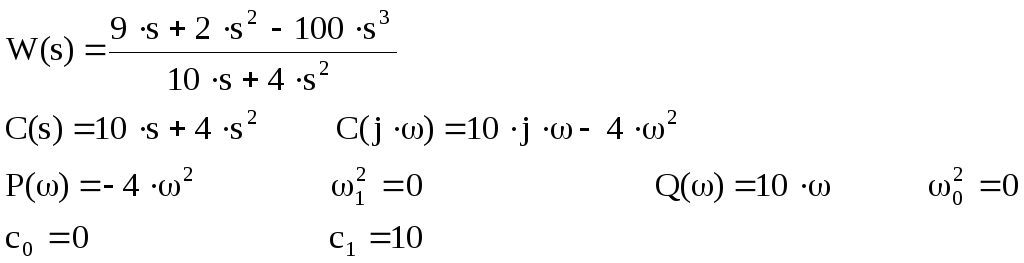 = -1

П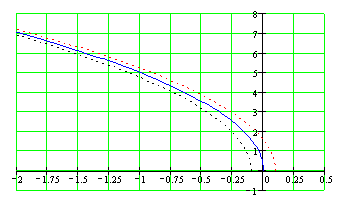 остроим годограф Михайлова:

Прохождение годографа через начало координат является необходимым, но не достаточным условием нейтральности полинома. Для разрешения граничной неопределенности используем метод вариации коэффициентов ХП, разрешив им изменяться .

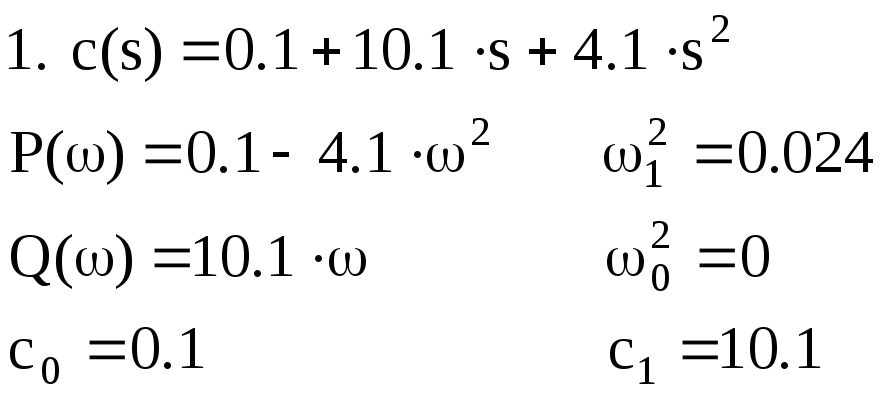
По годографу Михайлова для замкнутой системы видно, что суммарное изменение аргумента в квадрантах . Число правых корней . Число левых корней .

Так как , замкнутая система устойчива. Следовательно, исходная система нейтральна, так как хотя бы один из двух модифицированных полиномов, не проходящих через начало координат удовлетворяет условиям устойчивости.

K = 0.303

Построим годограф Михайлова:

Прохождение годографа через начало координат является необходимым, но не достаточным условием нейтральности полинома. Для разрешения граничной неопределенности используем метод вариации коэффициентов ХП, разрешив им изменяться .

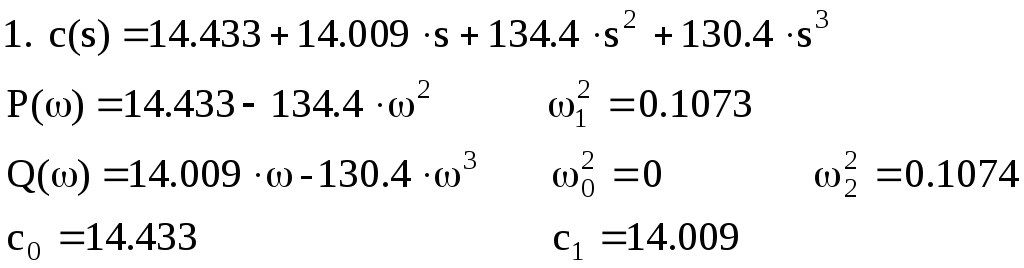
По годографу Михайлова для замкнутой системы видно, что суммарное изменение аргумента в квадрантах . Число правых корней . Число левых корней .

Так как , замкнутая система устойчива. Следовательно, исходная система нейтральна, так как хотя бы один из двух модифицированных полиномов, не проходящих через начало координат удовлетворяет условиям устойчивости.

K= -0.5

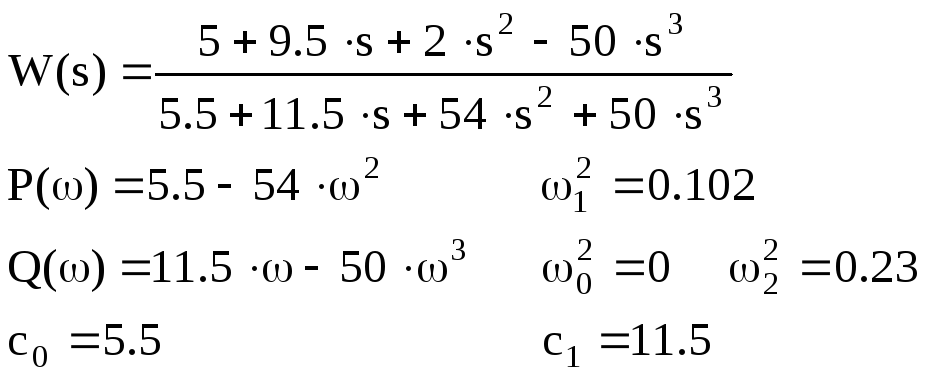
Условия выполняются.

Построим годограф Михайлова:

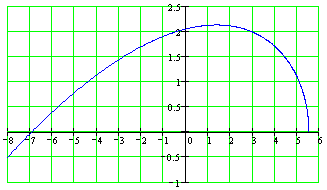
По годографу Михайлова для замкнутой системы видно, что суммарное изменение аргумента в квадрантах . Число правых корней . Число левых корней .

Так как , замкнутая система устойчива.

K= -2

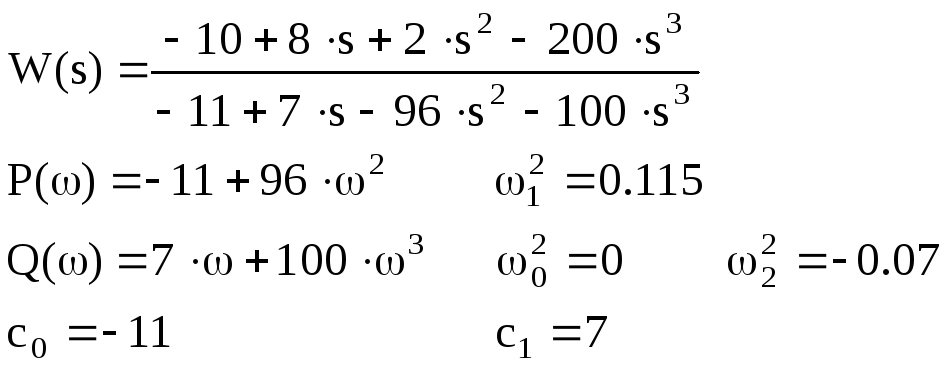
Условия не выполняются.

Построим годограф Михайлова:

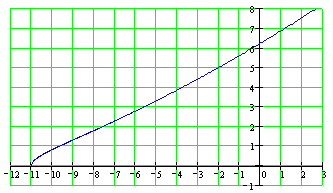
По годографу Михайлова для замкнутой системы видно, что суммарное изменение аргумента в квадрантах . Число правых корней . Число левых корней .

Так как , замкнутая система не устойчива.

K= 0.5

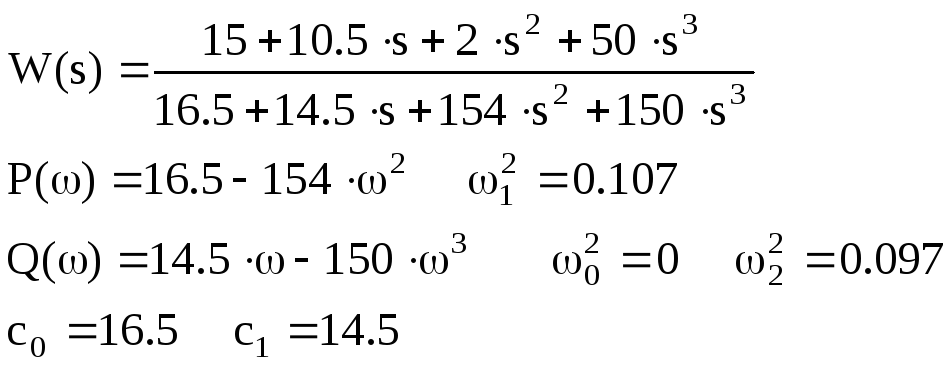
Условия не выполняются.

Построим годограф Михайлова:

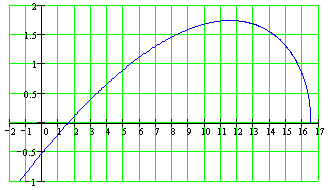
По годографу Михайлова для замкнутой системы видно, что суммарное изменение аргумента в квадрантах . Число правых корней . Число левых корней .

Так как , замкнутая система не устойчива.

Критерий устойчивости Найквиста.

Логарифмический:

Для устойчивости ЗС с контурной ПФ W_K(s), имеющей n₊ правых полюсов, необходимо и достаточно, чтобы на интервалах, где L_K(ω)>0, число пересечений Φ_K(ω) граничных уровней фазы составляло в сумме n₊/2.

Частотный:

Для устойчивости ЗС с контурной ПФ W_K(s), имеющей n₊ правых полюсов, необходимо и достаточно, чтобы годограф разомкнутого контура пересекал действительную ось левее точки Найквиста в сумме n₊/2 раз.

K= -1

Р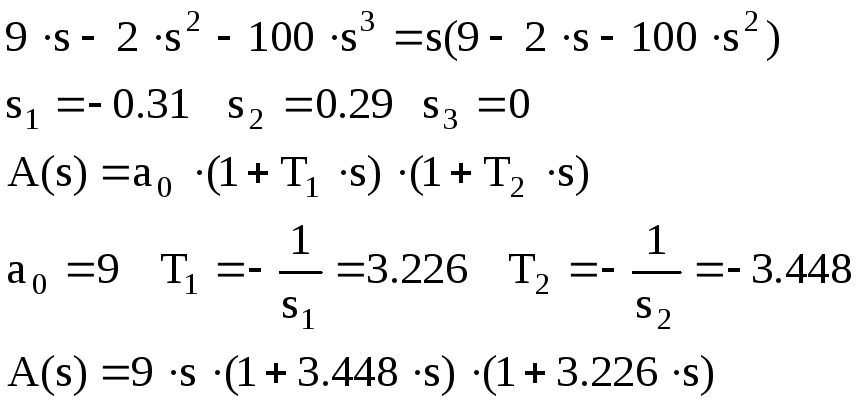азложим ПФ разомкнутой системы на типовые звенья:

1.

2.

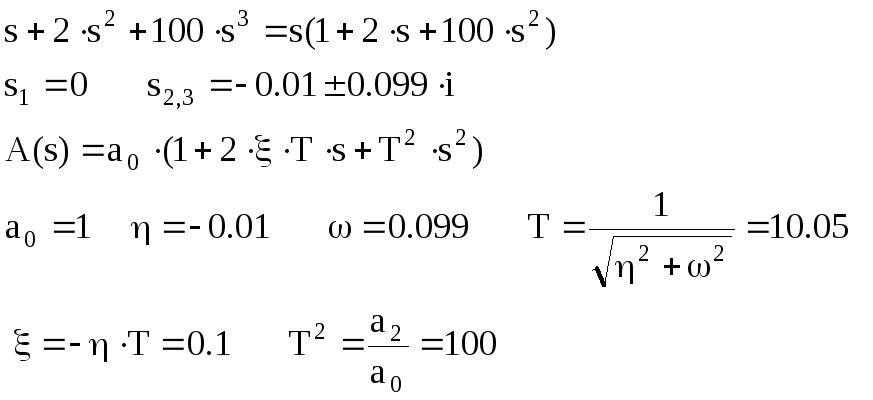
Разложим передаточную функцию на передаточные функции типовых звеньев:

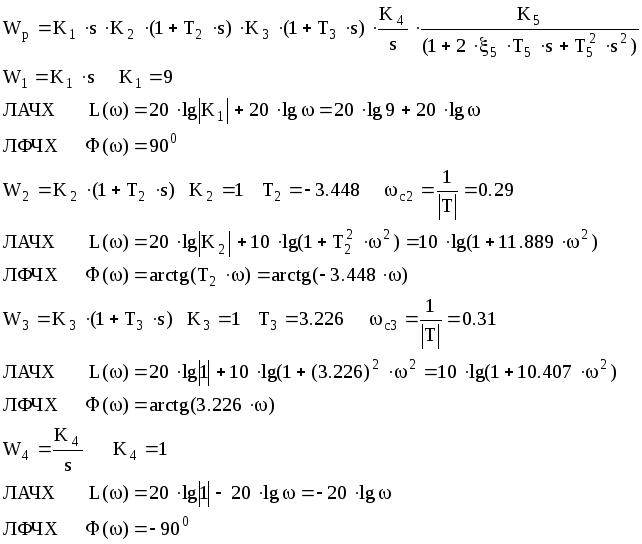
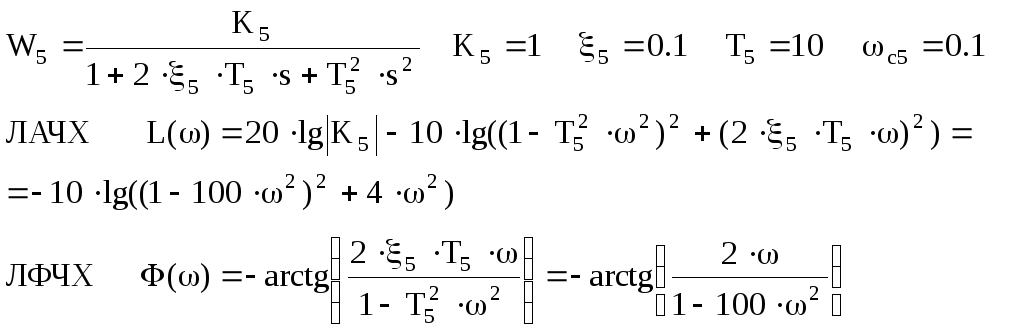
Построим ЛАЧХ:

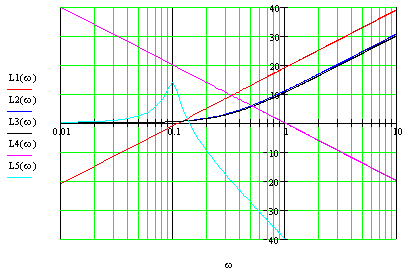
Результирующая ЛАЧХ:

Построим ЛФЧХ:

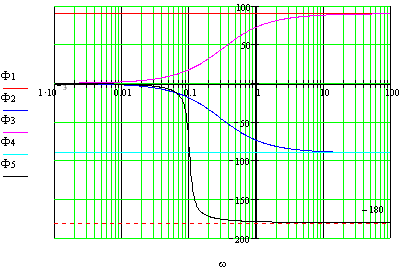
Результирующая ЛФЧХ:

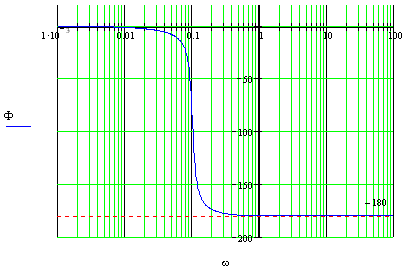
L(ω)>0 при любом ω. Φ(ω)=180⁰ при . Небольшое смещение L(ω) вниз дает необходимую для ее устойчивости сумму переходов Φ(ω) равную 0 через уровень φ_гр= -180⁰, следовательно, ЗС находится на границе устойчивости.

Построим годограф:

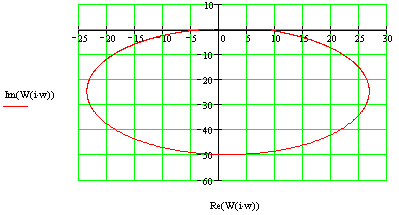
Годограф проходит через точку Найквиста и при небольшой вариации формы удовлетворяет критериям устойчивости, следовательно, ЗС находится на границе устойчивости.

K= 0.303

Р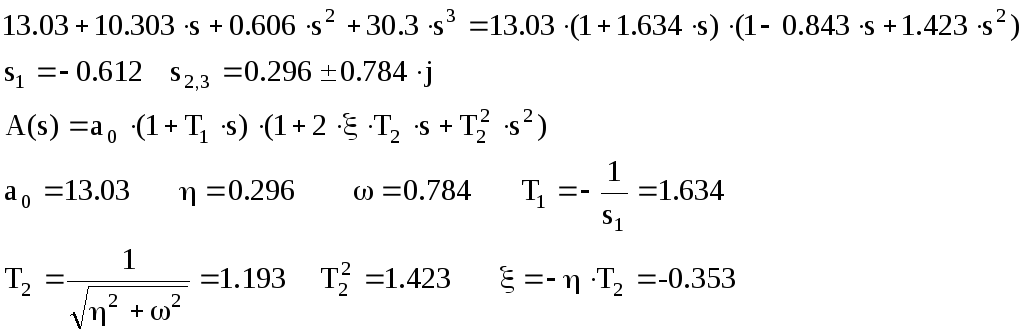азложим ПФ разомкнутой системы на типовые звенья:

1.

2.

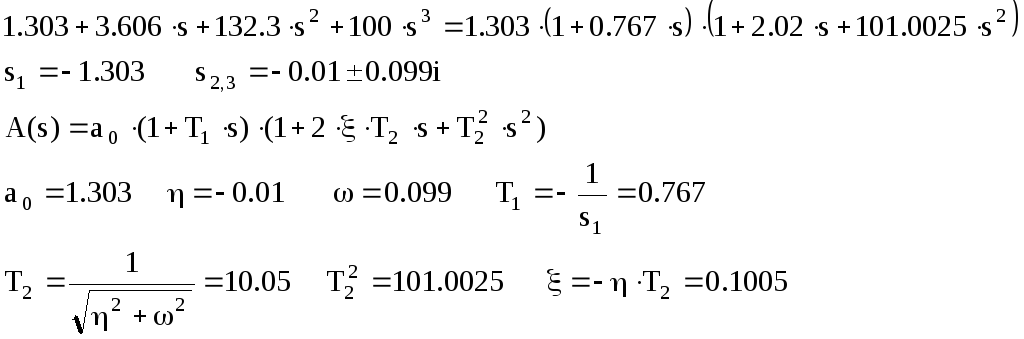
Разложим передаточную функцию на передаточные функции типовых звеньев:

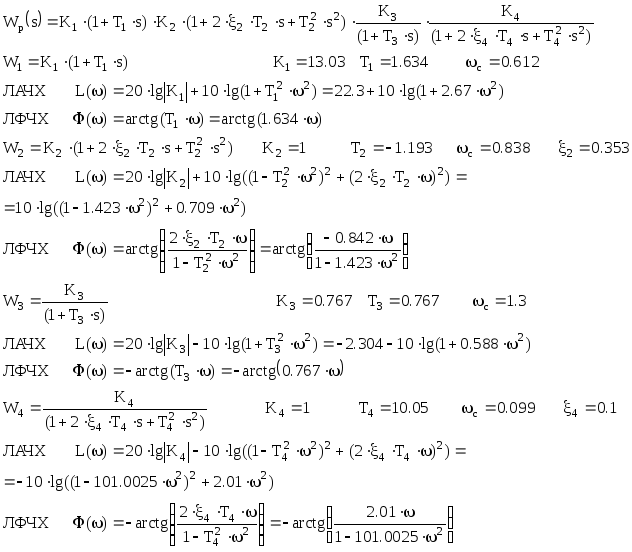
Построим ЛАЧХ:

Результирующая ЛАЧХ:

Построим ЛФЧХ:

Результирующая ЛФЧХ:

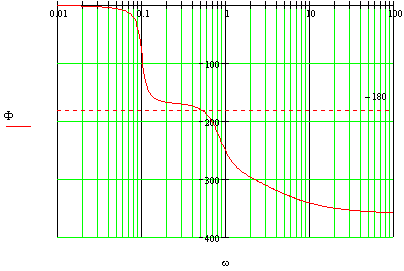
L(ω)>0 при ω<0.4. Φ(ω)=180⁰ при . Небольшое смещение L(ω) вверх дает необходимую для ее устойчивости сумму переходов Φ(ω) равную 0 через уровень φ_гр= -180⁰, следовательно, ЗС находится на границе устойчивости.

Построим годограф:

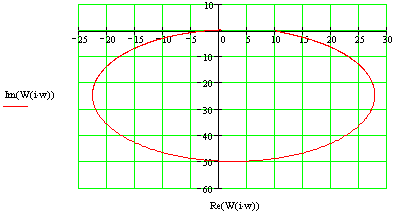
Годограф проходит через точку Найквиста и при небольшой вариации формы удовлетворяет критериям устойчивости, следовательно, ЗС находится на границе устойчивости.

K= -0.5

Р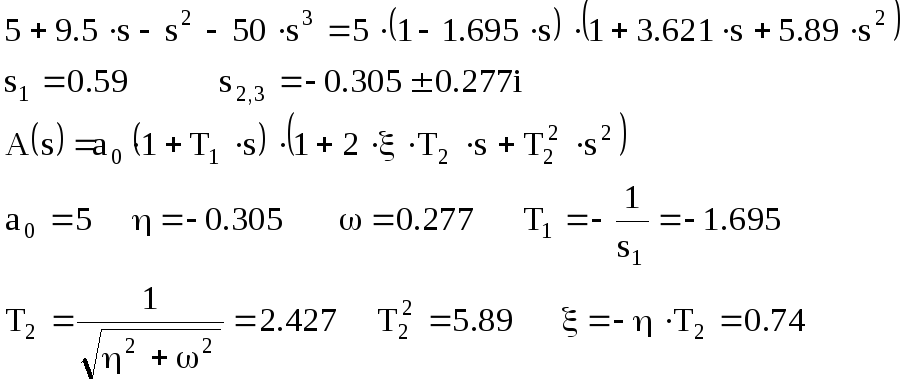азложим ПФ разомкнутой системы на типовые звенья:

1.

2.

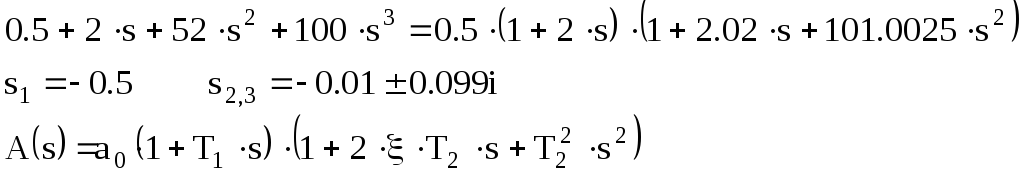
Разложим передаточную функцию на передаточные функции типовых звеньев:

Построим ЛАЧХ:

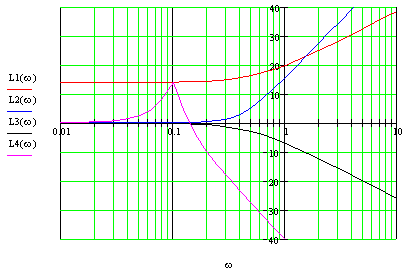
Результирующая ЛАЧХ:

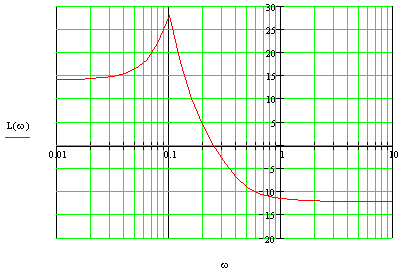
Построим ЛФЧХ:

Результирующая ЛФЧХ:

Ф(ω) не пересекает граничные уровни на любом интервале частот, где L(ω)>0, следовательно, ЗС устойчива.

Построим годограф:

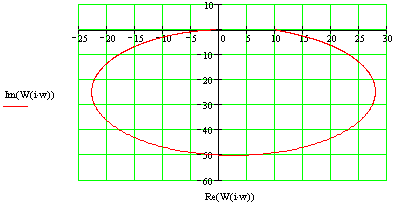
Годограф охватывает точку Найквиста, следовательно, ЗС устойчива.

K= -2

Р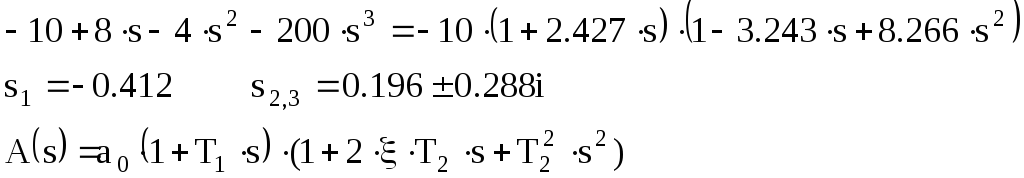азложим ПФ разомкнутой системы на типовые звенья:

1.

2.

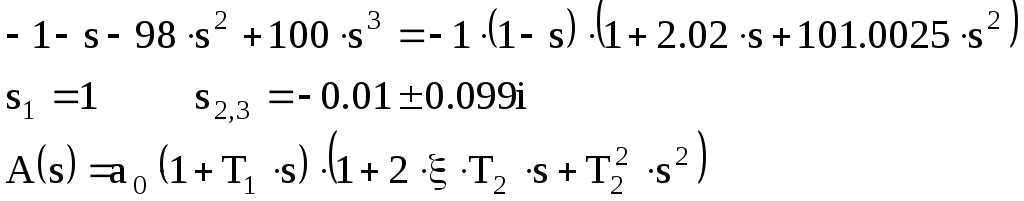
Разложим передаточную функцию на передаточные функции типовых звеньев:

Построим ЛАЧХ:

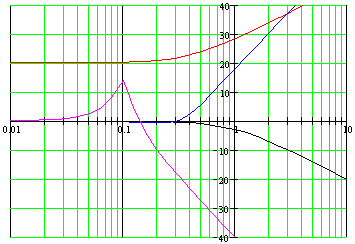
Результирующая ЛАЧХ:

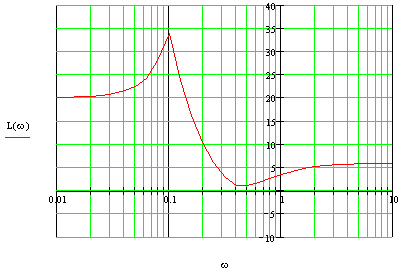
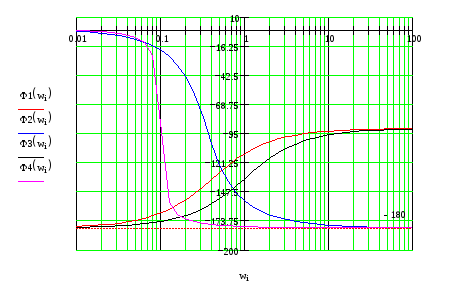
Построим ЛФЧХ:

Результирующая ЛФЧХ:

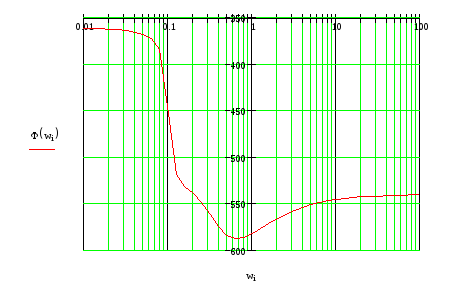
L(ω)>0 на всех интервалах частот, следовательно, Ф(ω) пересекает граничный уровень фазы φ_гр= –360^о, следовательно, система неустойчива.

Построим годограф:

Годограф не охватывает точку Найквиста, следовательно, ЗС не устойчива.

K= 0.5

Р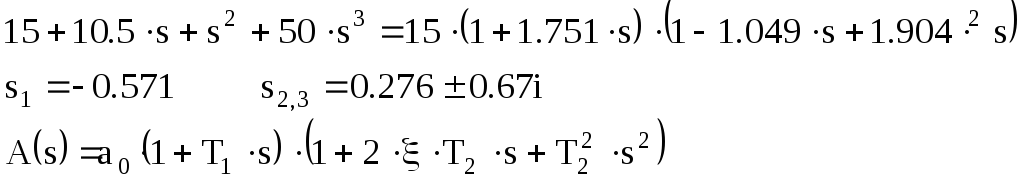азложим ПФ разомкнутой системы на типовые звенья:

1.

2.

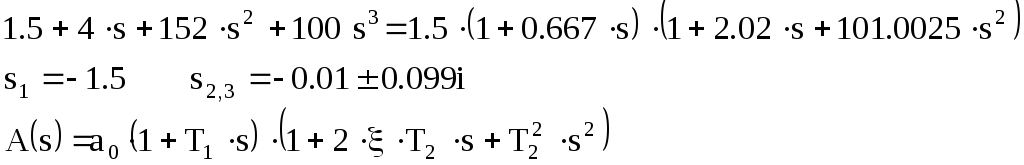
Разложим передаточную функцию на передаточные функции типовых звеньев:

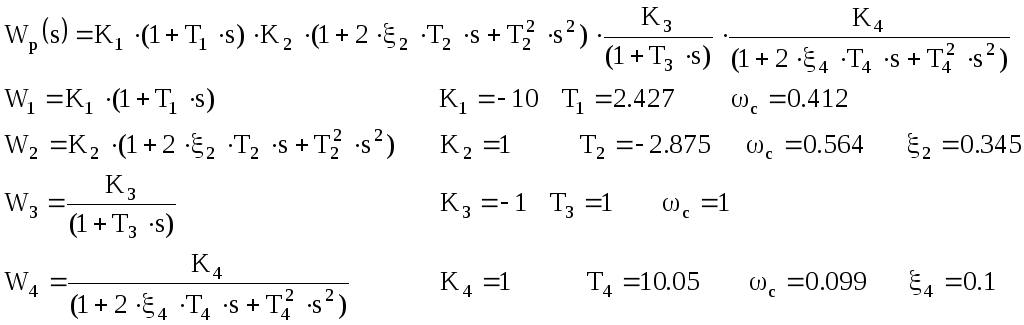
Построим ЛАЧХ:

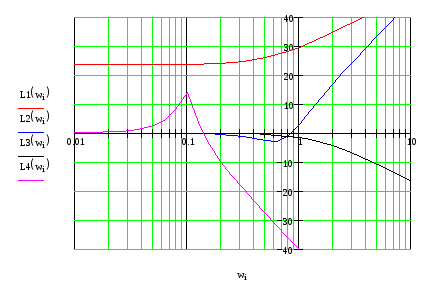
Результирующая ЛАЧХ:

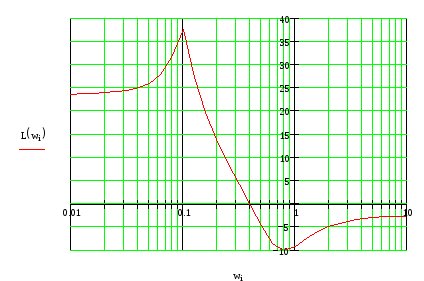
П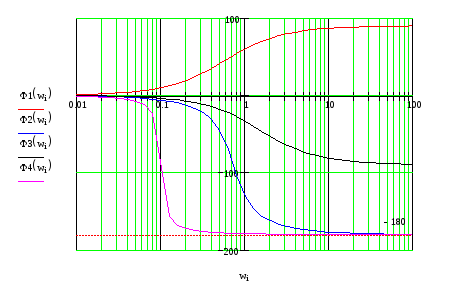 остроим ЛФЧХ:

Результирующая ЛФЧХ:

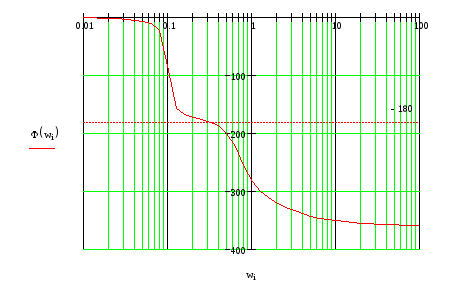
L(ω)>0 при ω<0.5, Ф(ω) пересекает граничный уровень -180⁰ , следовательно, ЗС не устойчива.

Построим годограф:

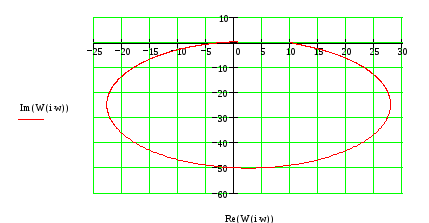
Годограф не охватывает точку Найквиста, следовательно, ЗС не устойчива.

8. Выбрать из набора параметров значение, при котором разомкнутая система устойчива, получить числовую ПФ системы с этим параметром и построить каноническую схему моделирования разомкнутой системы на операционных усилителях.

Построим каноническую схему моделирования разомкнутой системы на операционных усилителях для К=-0,5. ПФ при этом:

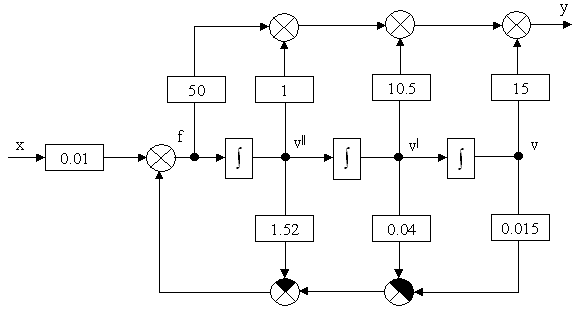
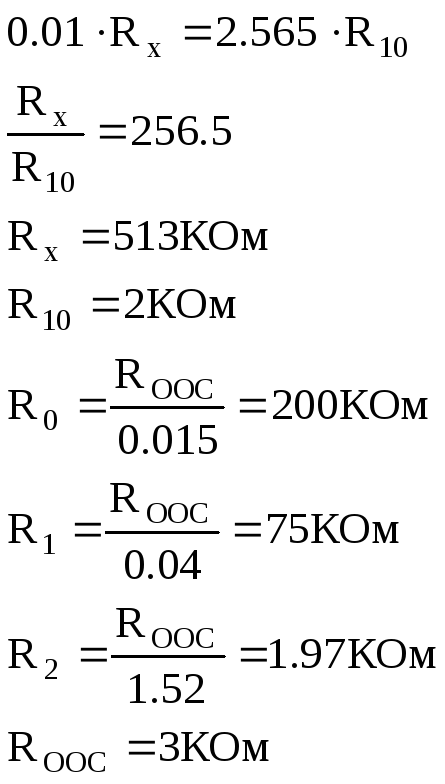
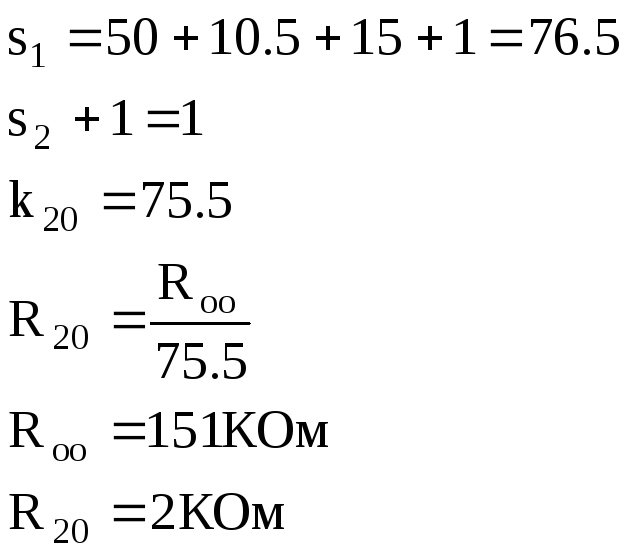
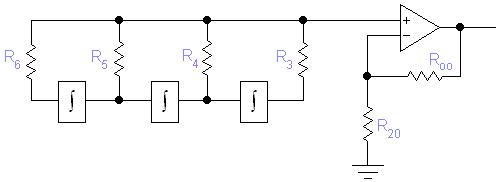
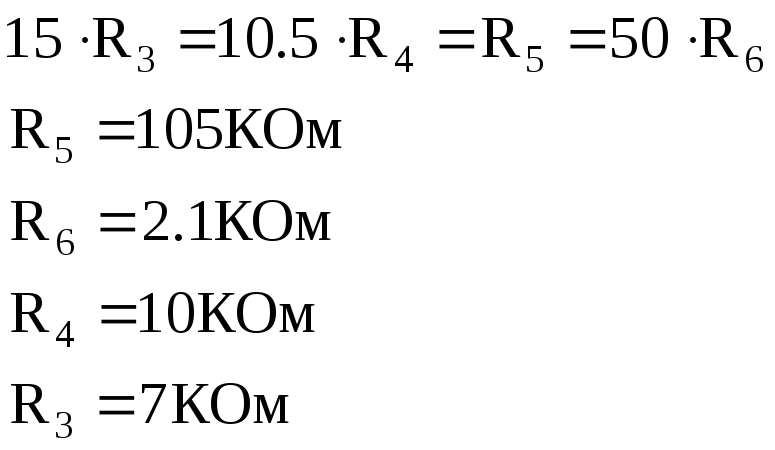
Схему будем строить на не инвертирующих интеграторах.

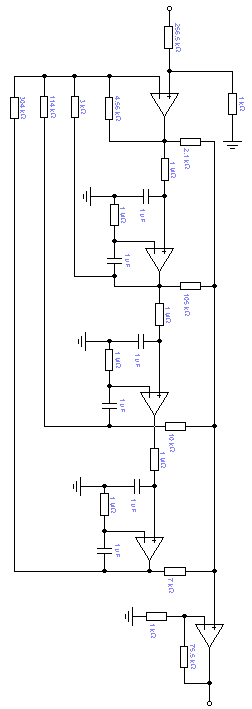
9. Получить оценки качества временных характеристик разомкнутой системы спектральными и частотными методами.

Разложим ПФ РС на сомножители:

Корни и полюсы полинома:

Спектральные оценки качества

1. Степень устойчивости . Для К=0.5 .

2. Степень быстродействия . Для К=0.5 .

3. Степень жесткости . Для К=0.5 .

4. Степень колебательности . Для К=0.5 .