курсовая работа / tau-zibben-auf / r-TAU-kursovik-var-02 / TAU3

3. Исследование устойчивости разомкнутой системы от буквенного параметра методами Гурвица и Михайлова.

3.1. Метод Гурвица.

Передаточная функция разомкнутой системы имеет вид:

,

отсюда характеристический полином для разомкнутой системы:

Корни полинома:

Матрица Гурвица:

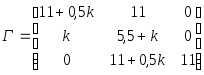
Для характеристического полинома третьей степени условием устойчивости является

, то есть , и должны быть одного знака и .

Находим второй минор матрицы Гурвица:

Так как , то для нахождения границ устойчивости необходимо решить систему неравенств:

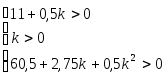
Так как уравнение не имеет действительных корней и коэффициент при больше нуля, то последнее неравенство системы выполняется при любых значениях k. Тогда система неравенств становится следующей:

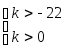, ее решением является , то есть разомкнутая система будет устойчива при .

3.2. Метод Михайлова.

Передаточная функция разомкнутой системы имеет вид:

,

отсюда характеристический полином для разомкнутой системы:

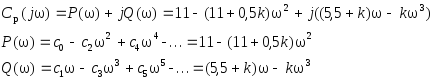
Полиномы и имеют корни:

По критерию Михайлова для устойчивости системы необходимо, чтобы корни чередовались по возрастанию: и коэффициенты её характеристического полинома были одного знака и ненулевые. Отсюда следует, что для устойчивости системы в нашем случае необходимо выполнение неравенства:

Найдем значения k, при которых неравенство верно:

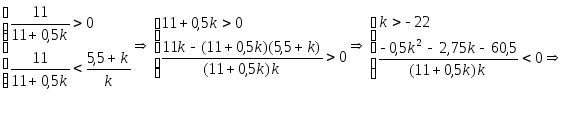
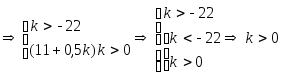
То есть условия устойчивости системы выполняются при k>0. Случай с не рассматриваем, так как .

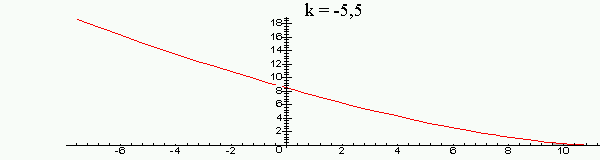
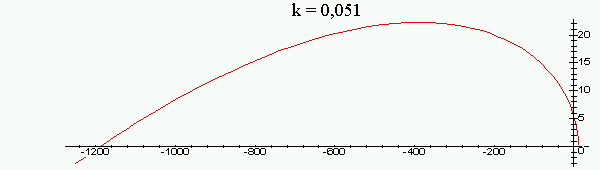
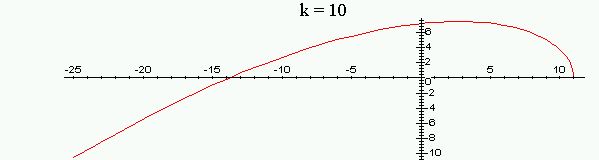
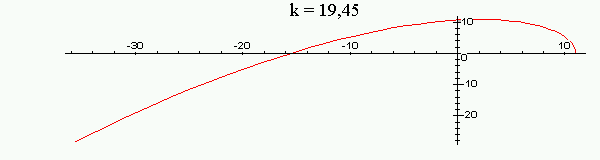
Рассмотрим годограф Михайлова для значений , , , и . Из графика видно, что при , , и годограф последовательно обходит три квадранта против часовой стрелки, то есть полином устойчив. При полином не устойчив.