курсовая работа / tau-zibben-auf / r-TAU-kursovik-var-02 / TAU7_MIX

7.6. Проверка устойчивости системы методом Михайлова.

Передаточная функция разомкнутой системы:

Передаточная функция системы с единичной отрицательной обратной связью имеет вид:

отсюда характеристический полином для замкнутой единичной ООС системы:

Полиномы и имеют корни:

По критерию Михайлова для устойчивости системы необходимо, чтобы корни чередовались по возрастанию: и коэффициенты её характеристического полинома были одного знака и ненулевые. Отсюда следует, что для устойчивости системы в нашем случае необходимо выполнение неравенства:

Найдем значения k, при которых неравенство верно:

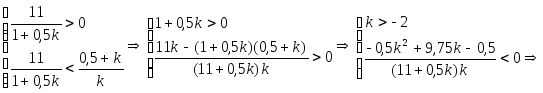
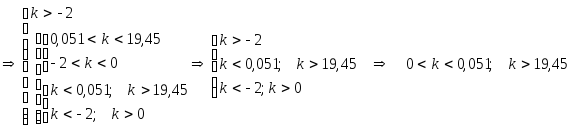
То есть условия устойчивости системы выполняются при и . Случай с не рассматриваем, так как .

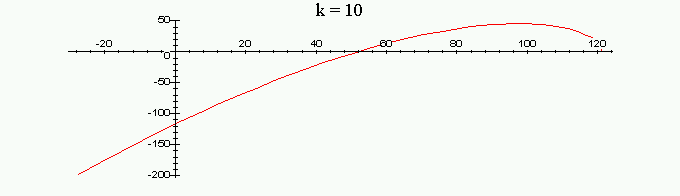
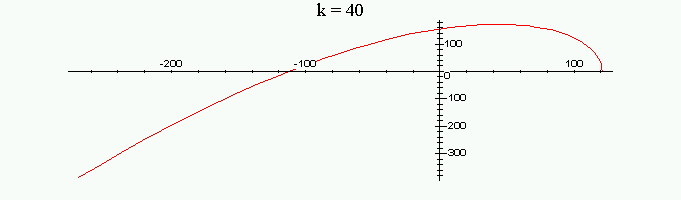
Рассмотрим годограф Михайлова для значений , , , и . Из графиков видно, что при годограф последовательно обходит три квадранта против часовой стрелки, то есть полином устойчив. При и полином не устойчив. При и годограф проходит через начало координат и система замкнутая единичной ООС находится на границе устойчивости.