5. Исследовать устойчивость замкнутой системы от буквенного параметра методами Гурвица и Рауса. Получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.
Критерий Рауса-Гурвица:
Построим матрицу Гурвица:
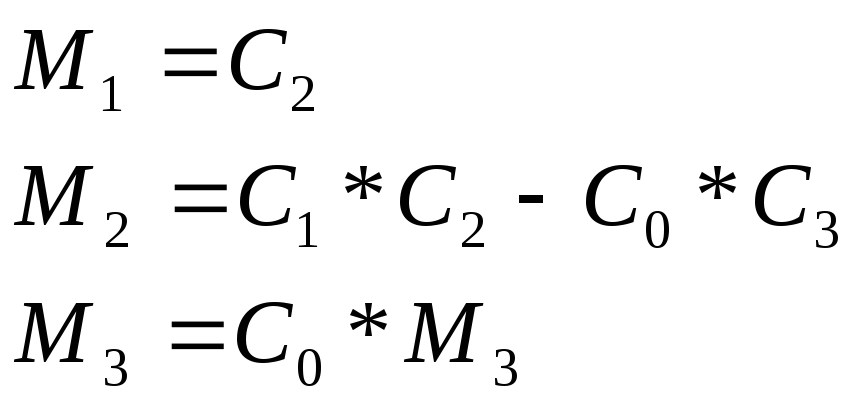
Для
устойчивости действительного полинома
необходимо и достаточно, чтобы все
элементы последовательности
были
одного знака, то есть
Если
,
то все главные миноры должны быть
положительны. Если
,
то знаки миноров должны чередоваться
, начиная с
.
Работаем с ХП ПФ замкнутой системы:
Условие устойчивости:
1) 11+11k>0 1122k+1100>0 1100k>0
k>-1 k>-0.98 k>0
Получили k>0.
2) 11+11k<0 1122k+1100<0 1100k<0
k<-1 k<-0.98 k<0
Получили k<-1.
3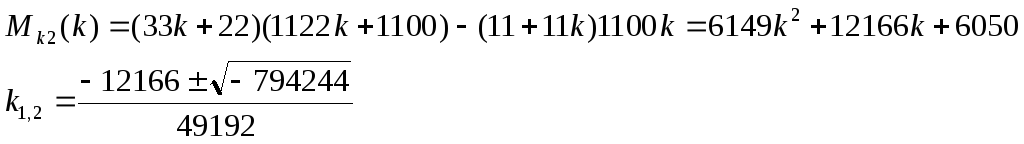
)
Коэффициенты полученного квадратного уравнения >0, значит ветви этой параболы направлены вверх. Она не имеет пересечений с осью k, следовательно k-любое число.
Объединяя ответы получим , что замкнутая система устойчива при k<-1 и k>0.
6. Cформировать набор значений параметра, включающий все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости замкнутой системы.
Учитывая, что ЗС является устойчивой, когда k<-1 и k>0, получим:
Значение, при которых система находится на границе устойчивости: k= -1
Значения, при котором ЗС является устойчивой: k=2 и k= -20
Значение, при которых ЗС находится в неустойчивом состоянии: k= -0.5
7.Для каждого значения параметра из набора построить частотные характеристики, необходимые для исследования устойчивости замкнутой системы от параметра по критериям Найквиста и Михайлова.
7.1 Построим годограф Михайлова для замкнутой системы с единичной отрицательной ОС для значений к=-20, к=-1, к=-0.5, к=2. Подставим эти значения к в мнимую и действительную часть ХП
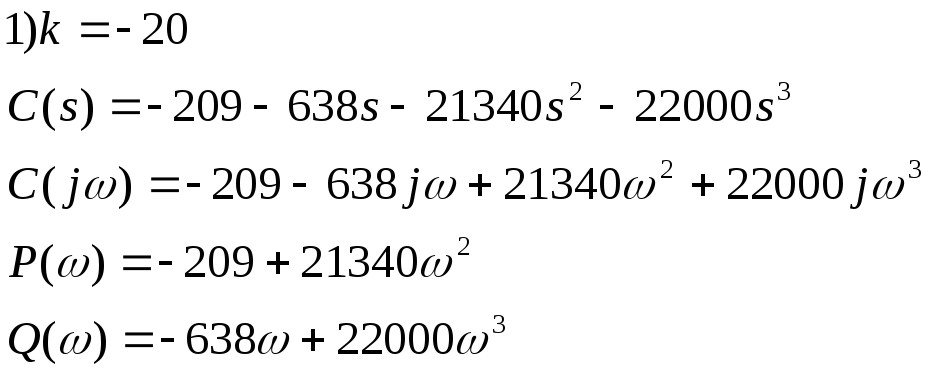
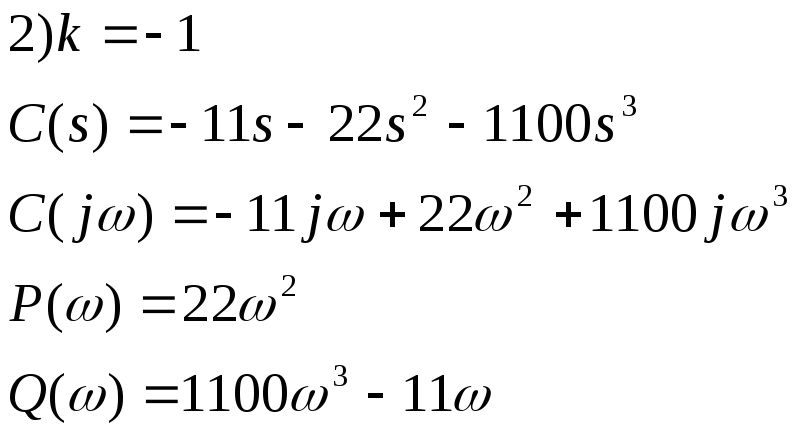
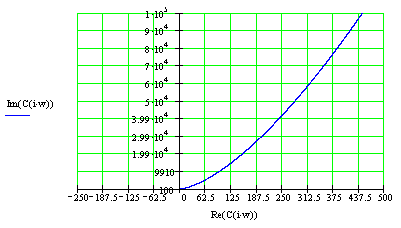
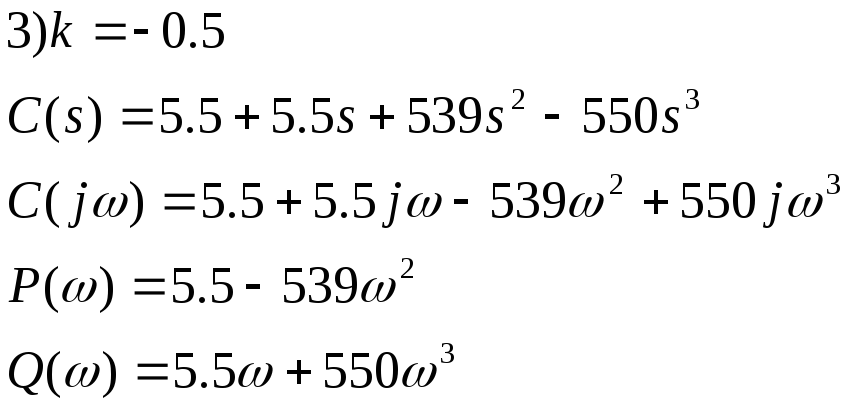
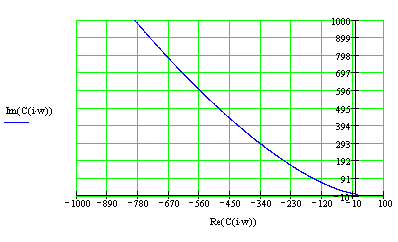
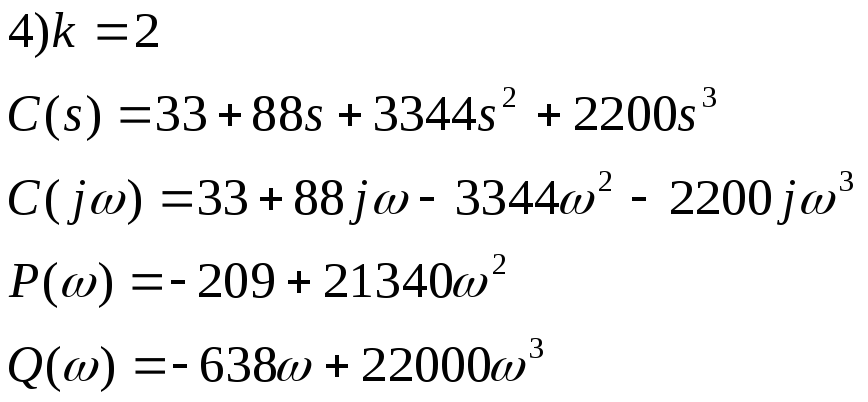
7.2)Критерий Найквиста
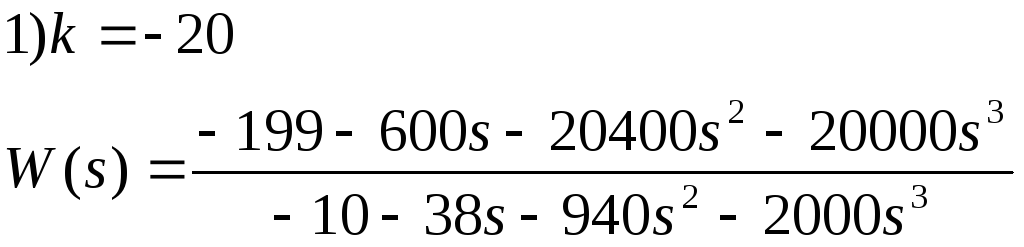
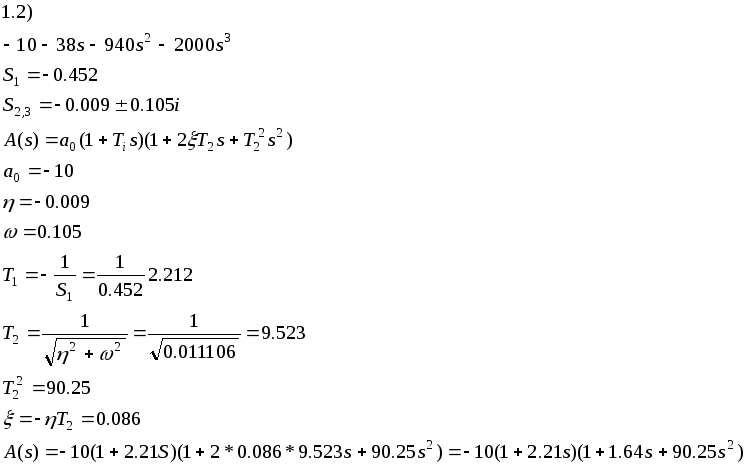
1.3) Разложим передаточную функцию на передаточные функции
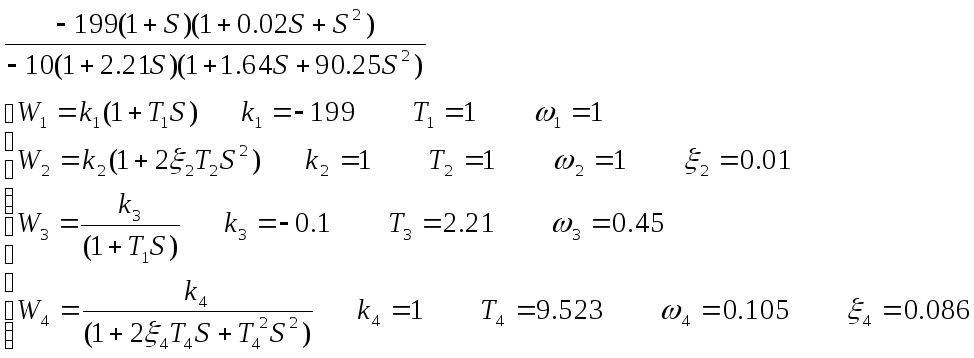
1.4)
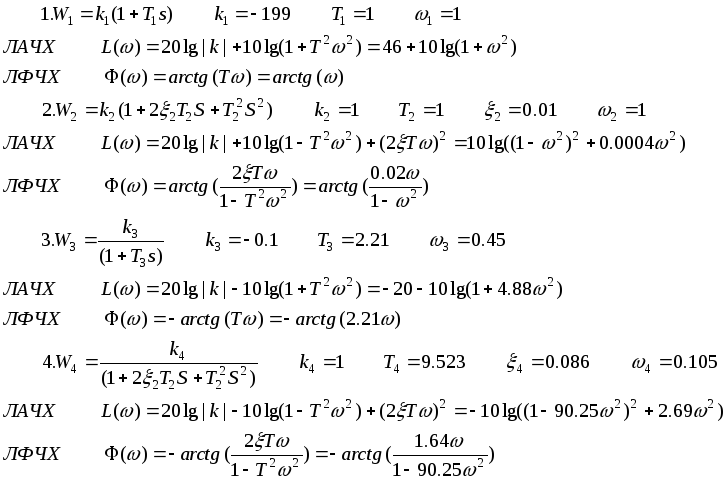
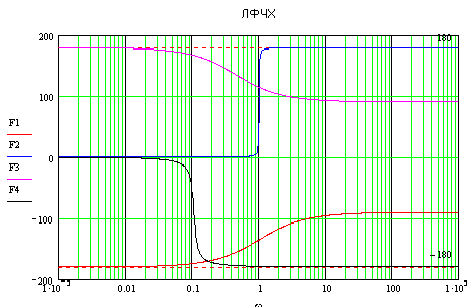
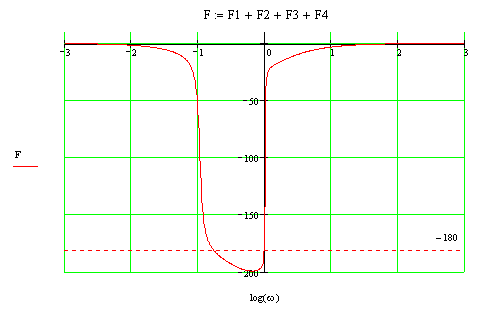
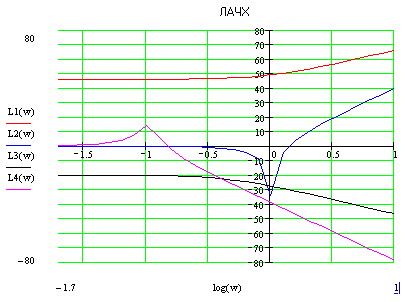
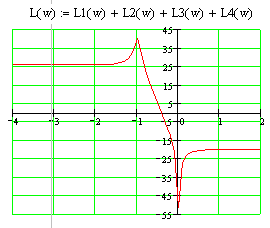
L(ω)>0
при ω<-0.4.
Φ(ω)=1800
при
и Φ(ω)=00
при
.
ЗС устойчива.
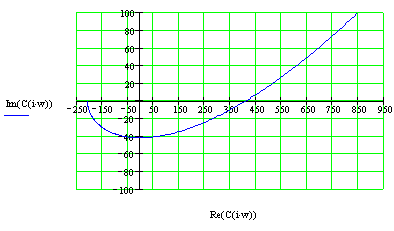
Построим годограф:
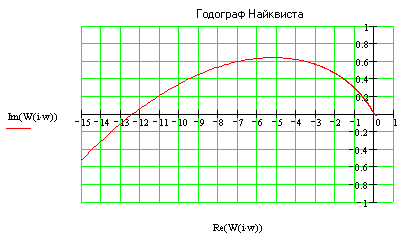
Годограф охватывает точку Найквиста, следовательно, ЗС устойчива.
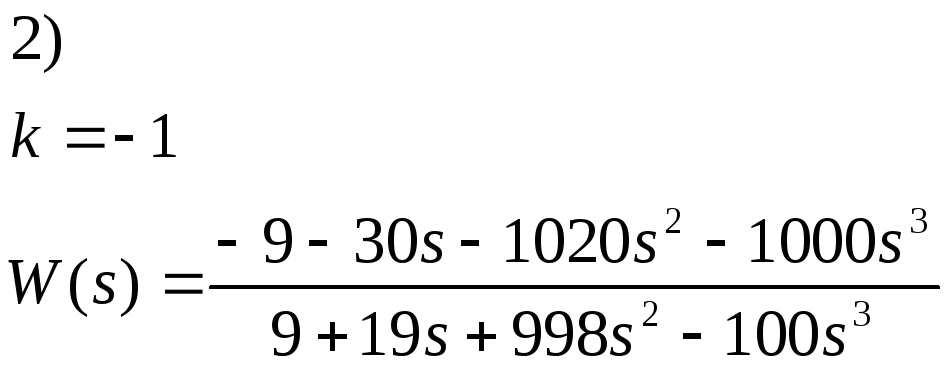
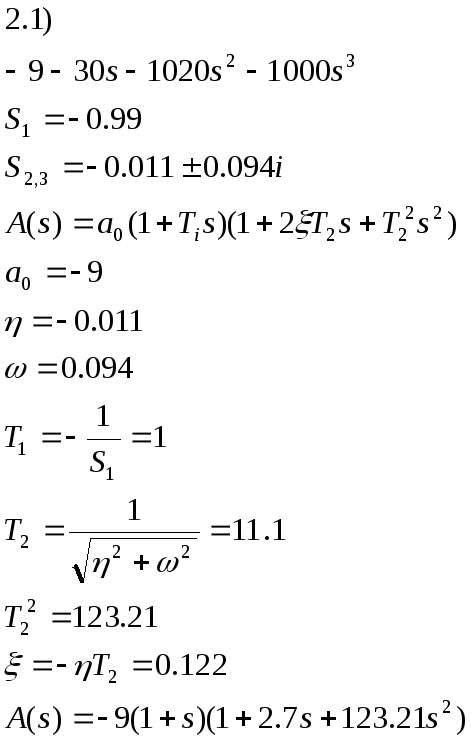
2.3) Разложим передаточную функцию на передаточные функции
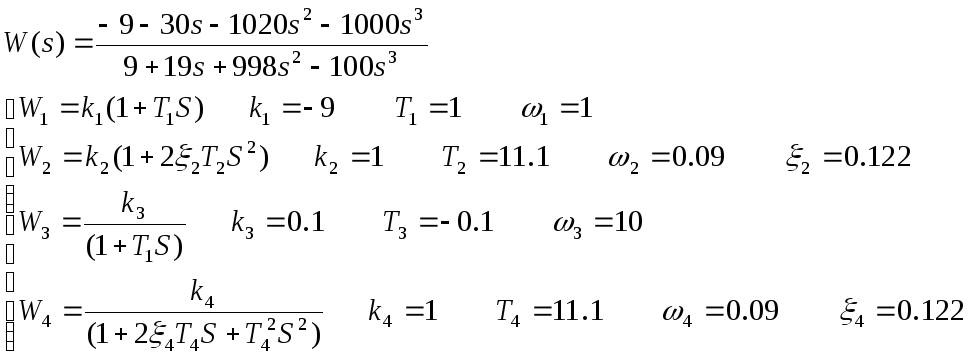
2.4)
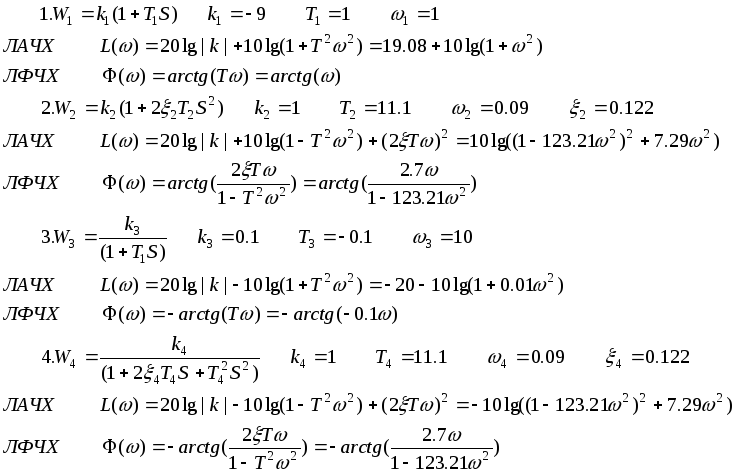
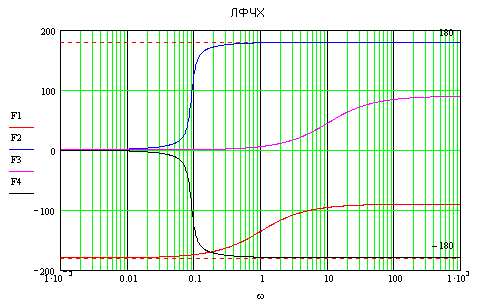
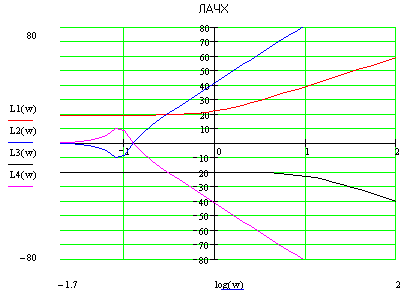
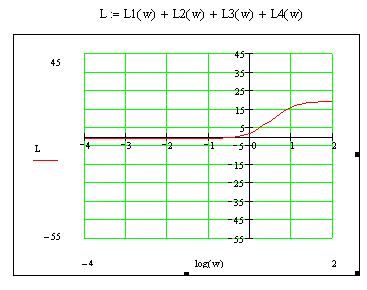
L(ω)>0
при
.
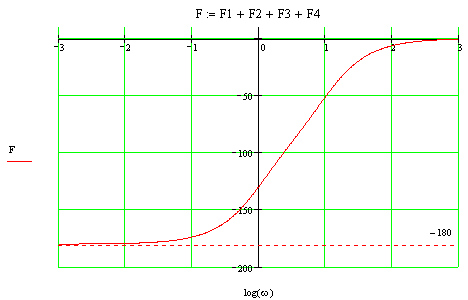
Φ(ω)=00
при
.
Небольшое смещение L(ω)
вниз дает необходимую для ее устойчивости
сумму переходов Φ(ω) равную 0 через
уровень φгр=
-1800,
следовательно, ЗС находится на границе
устойчивости.
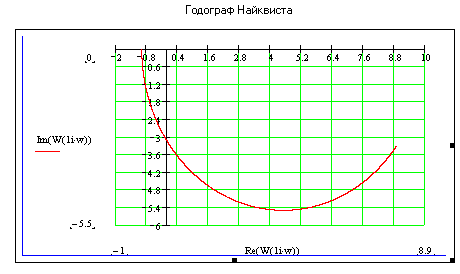
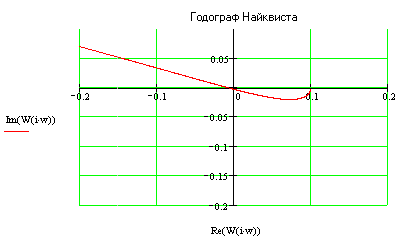
Годограф проходит через точку Найквиста и при небольшой вариации формы удовлетворяет критериям устойчивости, следовательно, ЗС находится на границе устойчивости.
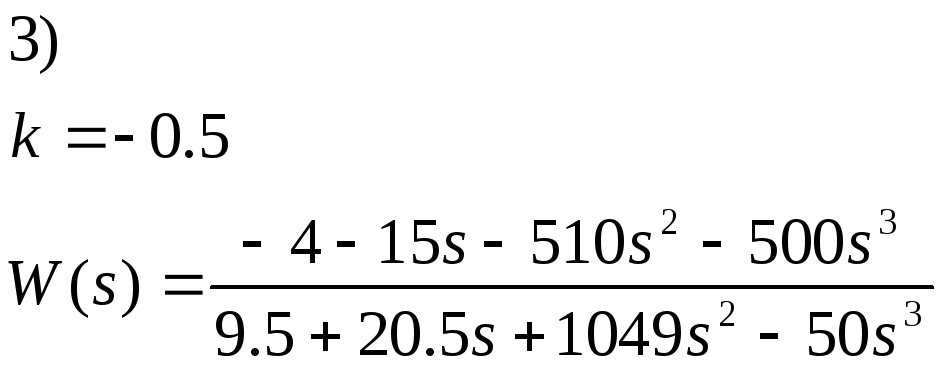
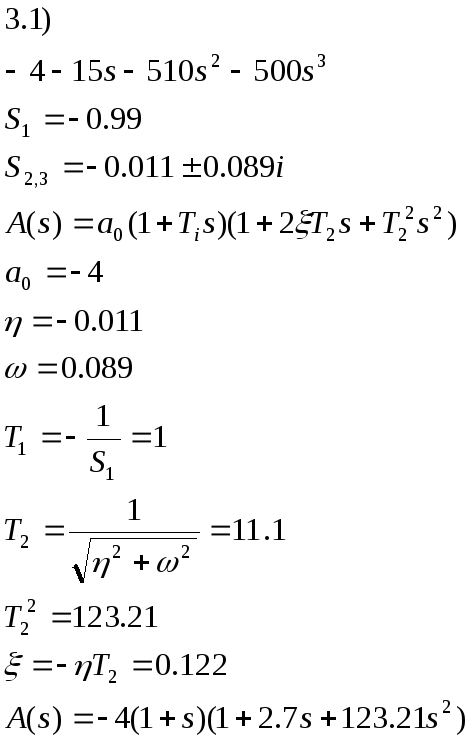
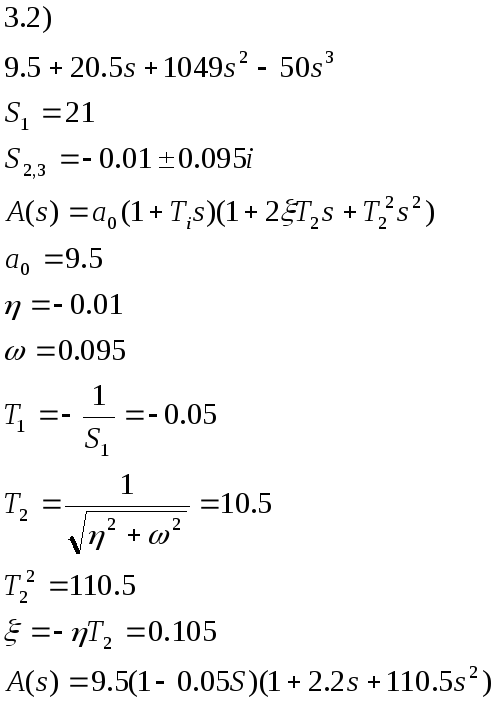
3.3) Разложим передаточную функцию на передаточные функции
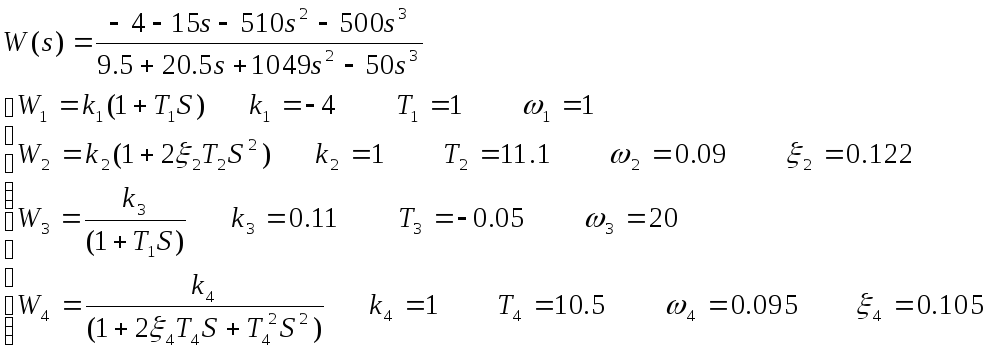
3.4)
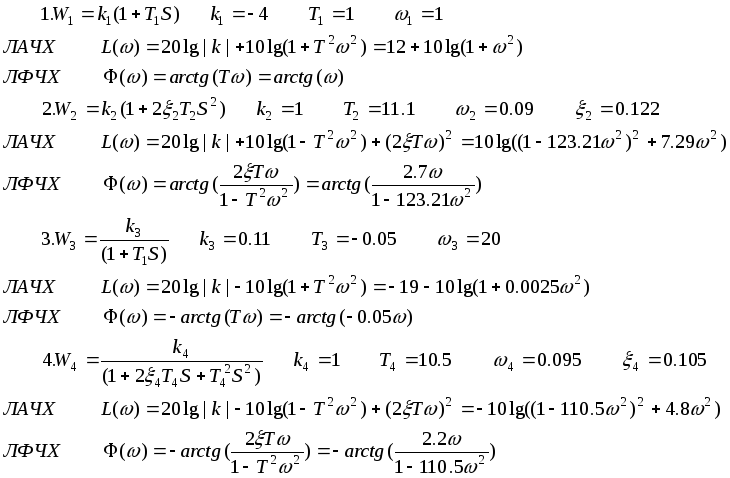
ЛФЧХ
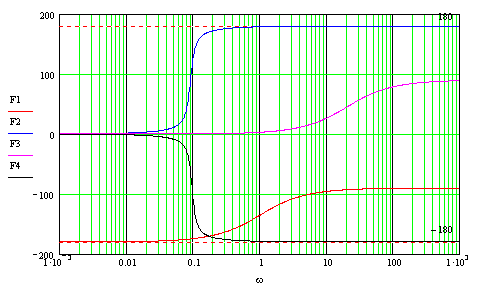
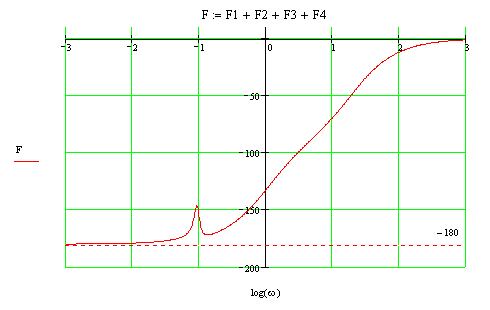
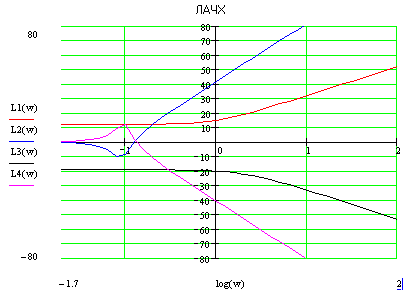
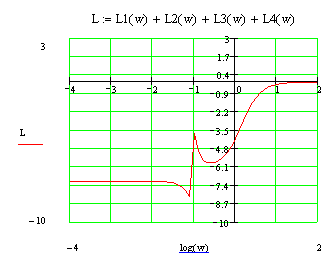
Нет
интервалов частот, где L(w)>0,
таким образом, число пересечений ЛФЧХ
граничных уровней фазы
в сумме составляет 0.Система не устойчива.
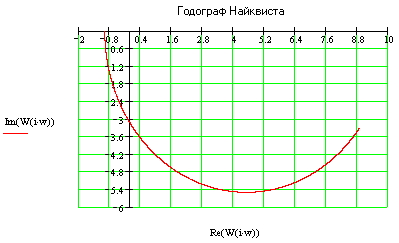
Годограф не охватывает точку Найквиста, следовательно, ЗС не устойчива.
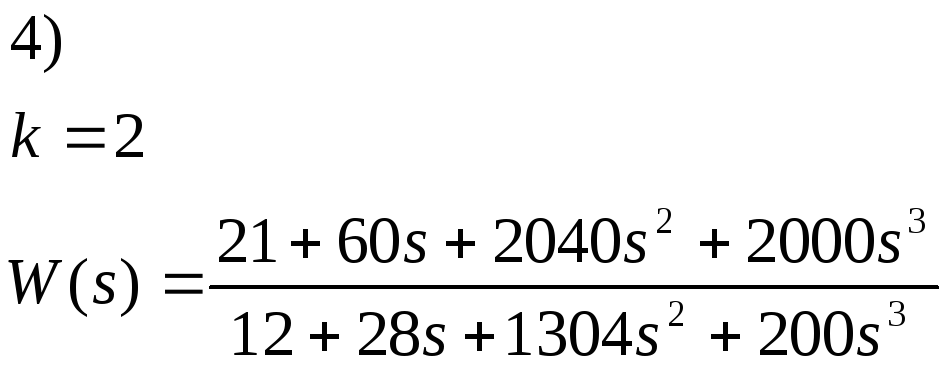
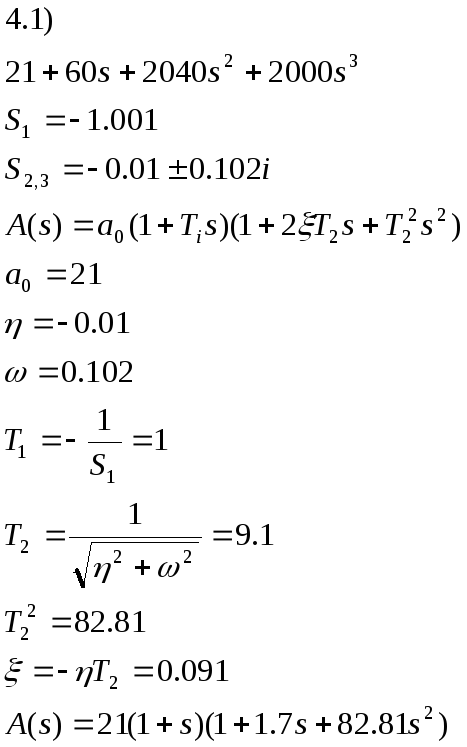
4.3) Разложим передаточную функцию на передаточные функции
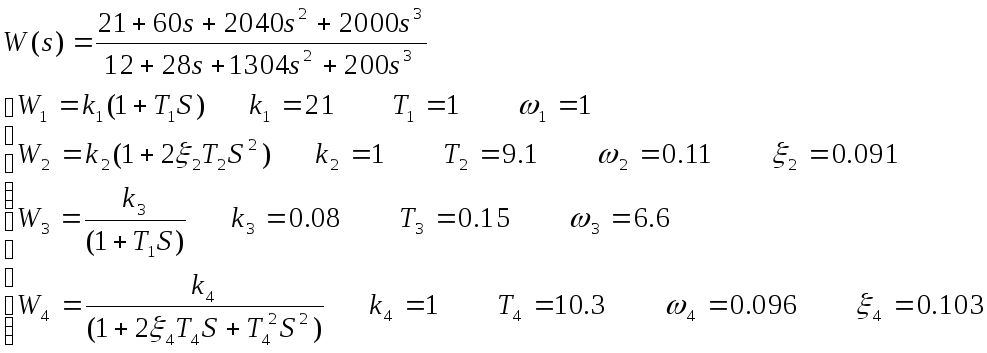
4.4)
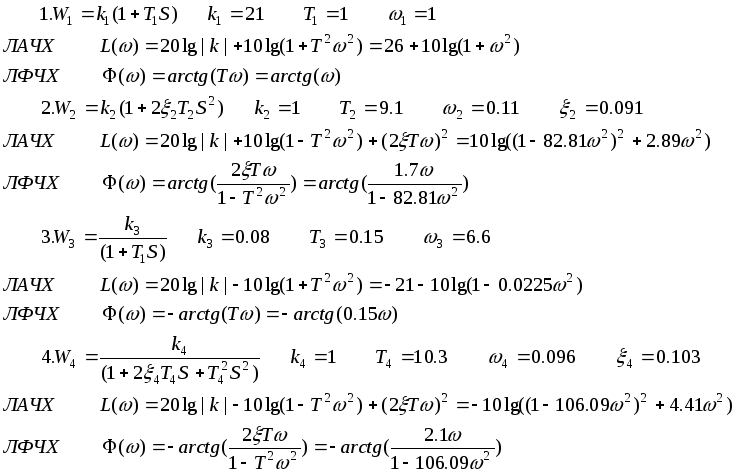
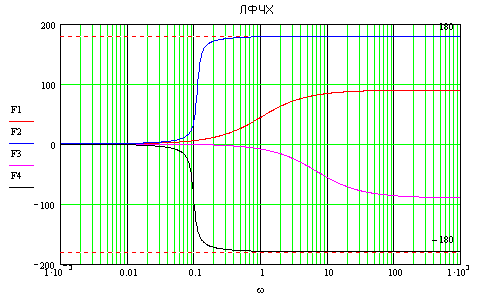
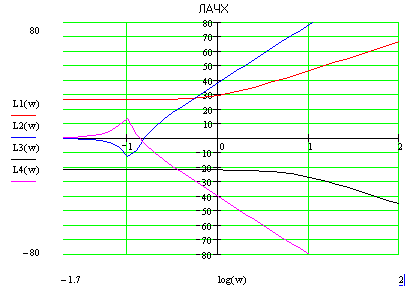
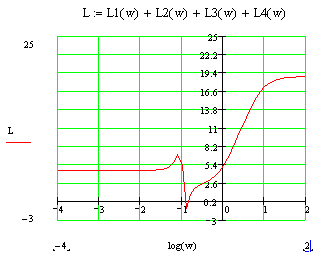
Ф(ω) не пересекает граничные уровни на любом интервале частот, где L(ω)>0, следовательно, ЗС устойчива.
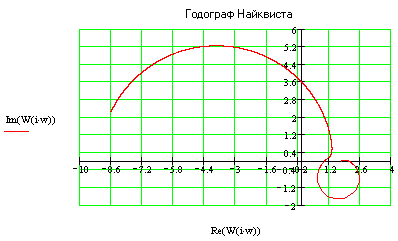
Годограф охватывает точку Найквиста, следовательно, ЗС устойчива.