
курсовая работа / курсач(ТАУ) / Курсач ИРИНА
.doc
ВВЕДЕНИЕ
Автоматическое регулирование представляет собой наиболее эффективный принцип автоматики при частичной автоматизации, когда технические средства автоматики осуществляют лишь простые функции управления, связанные с измерением, анализом, контролем различных физических величин и отработкой решений, принятых оператором в виде установок, программ или других сигналов управления.
Современные системы управления сложными объектами промышленной технологии строятся по иерархическому принципу. Это значит, что система управления такими объектами расчленяется на ряд систем, стоящих на разных уровнях подчинения. Система более высокого ранга, ориентируясь на общий (глобальный) критерий управления, выдает команды на включение или отключение отдельных локальных объектов, а также осуществляет выбор частных критериев управления этими объектами. Локальные системы управления осуществляют поддержание заданных оптимальных режимов как в пусковых, так и в нормальных эксплуатационных условиях. Являясь нижним иерархическим уровнем автоматических систем управления промышленными объектами локальные системы осуществляют функции измерения, контроля и регулирования основных технологических параметров, характеризующих состояние технологического процесса. Количество регулируемых параметров в отдельно взятой локальной системе управления невелико и составляет один или два параметра. Из общего числа систем управления современным производством локальные системы составляют около 80%. Качество работы локальных систем управления во многом определяет стабильность и качество выходного продукта, а, следовательно, и рентабельность производства.
1 Исследование линейной части системы
-
Описание принципиальной схемы САУ

1-аксиально-плунжерный насос; 2-вспомогательный (шиберный) насос; 3-подпорный клапан; 4-реверсивная коробка; 5-обратный клапан вспомогательного насоса; 6-предохранительный клапан вспомогательного насоса; 7-обратные клапаны полостей насоса высокого давления; 8-всасывающий клапан; 9-следящий золотник гидроусилителя; 10-гидроусилитель.
Рисунок 1- Гидравлическая схема насоса типа НАС
1.2 Функциональная схема насоса
На основе имеющейся функционально-принципиальной схемы построим функциональную схему.
Функциональная схема – это схема, состоящая из функциональных элементов, которые показывают их функциональное назначение при автоматическом управлении технологическим процессом и связь между ними.

Рисунок 2 - Функциональная схема насоса.
1.3 Построение структурной схемы насоса
На основе полученной функциональной схемы, задав численное значение сигналов, построим структурную схему системы.
Структурная схема системы автоматического управления отражает прохождение и преобразование сигналов в звеньях системы управления.
W1(p) W2(p) W3(p) W2(p)
W4(p)








W5(p) W2(p)



W1(p)- Передаточная функция бака;
W2(p)- Передаточная функция всасывающего клапана;
W3(p)- Передаточная функция насоса;
W4(p)- Передаточная функция гидроцилиндров;
W5(p)- Передаточная функция золотника;
Рисунок 3 - Структурная схема насоса.
Передаточная функция бака:

С учетом коэффициентов:
![]()
Передаточная функция всасывающего клапана:
![]()
С учетом коэффициентов:
![]()
Передаточная функция насоса:
![]()
С учетом коэффициентов:
![]()
Передаточная функция гидроцилиндров:
![]()
С учетом коэффициентов:
![]()
Передаточная функция золотника:
![]()
С учетом коэффициентов:
![]()
Таким образом передаточные функции элементов, входящих в структурную схему:
![]()
![]()
![]()
![]()
![]()
-
Преобразование структурной схемы.
Применяя правила преобразования структурных схем, упростим нашу схему.
Выражение для общей передаточной функции:
![]()
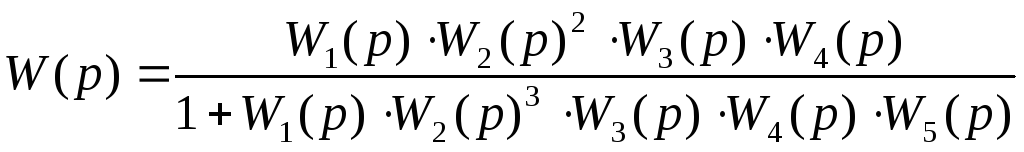
Используя программу MathCAD, подставив значения функций, получим
выражение общей для передаточной функции:

=![]()
-
Определение устойчивости системы по критерию Гурвица.
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными.
По коэффициентам характеристического уравнения составляется определитель Гурвица.
Для этого по главной диагонали определителя выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.
Составленный определитель называется главным определителем Гурвица, он имеет порядок совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и т.д. порядков их образования из главного определителя.
Вычисляя главный определитель и частные определители, Гурвиц устано-
вил, для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны. Если хотя бы один определитель отрицательный, то система неустойчива.
![]()
а0=6.05;
а1=13.2; а2=12.2; а3=8.13;
а4=4.21;
а5=1; а6=0;
а7=0.88∙![]()


∆1=а1=13.2 > 0
∆2
=
![]() =111.8535>
0
=111.8535>
0
∆3= =255.679
> 0
=255.679
> 0
∆4= =
=![]() <
0
<
0
Так как ∆4 отрицательна, то по критерию Гурвица САУ неустойчива. Это же следует из того, что вещественная часть корней характеристического уравнения положительна и, согласно теореме Ляпунова, САУ неустойчива.
-
Определение устойчивости системы по критерию Михайлова.
Необходимо, чтобы годограф Михайлова прошел последовательно все
квадранты.
Характеристическое уравнение имеет вид:
![]()
Получим характеристический вектор и выделим в нем вещественную и мнимую части.
![]()
![]()
Используя программу MathCAD, построим годограф Михайлова:



Рисунок 4 – Годограф Михайлова для системы насоса типа НАС
Из графика видно, что система является неустойчивой, т.к. годограф Михайлова не проходит последовательно все квадранты.
1.7 Построение переходного процесса
Переходная
функция - это реакция системы на
ступенчатое входное воздействие. Для
того, чтобы построить переходный процесс,
используем обратное преобразование
Лапласа от функции вида
![]()

-![]()
Переходная функция:
h (t)=
(t)=
![]()
,с


Рисунок 5 – График переходного процесса
Анализируя график, можно судить о том, что данная линейная система неустойчива. Прямые оценки качества системы определить невозможно.
-
Построение амплитудно-частотной характеристики системы
АЧХ строится для того, чтобы определить косвенные оценки качества системы.

![]()



,1/с
Рисунок 6 - График АЧХ
Определим косвенные оценки качества системы:
- амплитуда при нулевой частоте A(0)=0;
- максимальная амплитуда Аmax=0.72;
- резонансная частота - это частота, при которой амплитуда максимальна
wp=10 Гц;
- частота среза - это частота, при которой амплитуда равна 0.1
wcp=16.36 Гц;
-
полоса пропускания – это диапазон
частот от w1
до w2,
который определяется при срезе величиной
![]() графика АЧХ
графика АЧХ
w1=8 Гц, w2=11.64 Гц , следовательно wпр=3.64 Гц;
-
период колебаний
![]() =0.63
с;
=0.63
с;
-
показатель колебательности
![]() = ∞;
= ∞;
-
величина перерегулирования
![]() ,
невозможно определить;
,
невозможно определить;
-
время регулирования
![]() =0.768
с
=0.768
с
![]() =1.885
с
=1.885
с
![]()
![]() с.
с.
-
Определение запаса устойчивости по логарифмической амплитудно-частотной характеристике и логарифмической фазо-частотной характеристике.

По данной передаточной функции построим ЛАЧХ и ЛФЧХ, выделив реальную и мнимую часть.
![]()
![]()
![]()
![]()
Аппроксимируем ЛАЧХ стандартными наклонами и определим по ним вид передаточной функции:
 ,
где
,
где







Рисунок 7 – График ЛАЧХ



Рисунок 8 – График ЛФЧХ
Запасы устойчивости по амплитуде и частоте определить невозможно, т.к. система является неустойчивой. Это видно по графикам: ЛАЧХ не пересекает нулевую амплитуду, а ЛФЧХ не пересекает -180о.
|
|
|
|
|
|
|
Лист |
|
|
|
|
|
|
|
|
|
Изм |
Лист |
№ докум |
Подп. |
Дата. |
